При больших емкостях (свыше 0,1 мкФ) качество диэлектрика конденсаторов часто характеризуют произведением сопротивления изоляции конденсатора на его емкость (ЯизС), которое называется постоянной времени конденсатора и выражается в мегомах на микрофараду (МОм • мкФ), в омах на фараду (Ом-Ф) или в секундах

В. А-с

Ом-Ф = -

= С.

В реальном конденсаторе зарядный ток спадает до нуля значительно медленнее, чем в идеальном конденсаторе, что обусловлено наличием дополнительного зарядного тока конденсатора, возникающего в результате относительно медленного перемещения электрических зарядов в толще диэлектрика (межслойная поляризация и т. д.), называемого током абсорбции. Этот ток сопровождает ток утечки. В зависимости от свойств диэлектрика спадание абсорбционного тока до нуля происходит в различные промежутки времени, достигающие 30-60 мин, после чего через конденсатор будет проходить только ток утечки.

Обычно, чтобы определить сопротивление изоляции, , ток измеряют через минуту после подачи напряжения на конденсатор. Поэтому при вычислениях получают некоторые условные значения сопротивления изоляции, которые из-за тока абсорбции могут быть значительно занижены по сравнению с величинами, определяемыми только током утечки. С наличием тока абсорбции связано также уменьшение емкости конденсатора при повышении рабочей частоты и быстрой смене циклов заряд-разряд.

Сопротивление диэлектриков зависит от влажности и температуры окружающей среды: с их увеличением сопротивление диэлектриков резко уменьшается. В некоторых случаях на величину сопротивления диэлектриков влияет напряженность электрического поля.

§ 6. Конденсаторы в цепи постоянного тока

При подключении к конденсатору постоянного напряжения и между его обкладками создается электрическое поле, под действием которого диэлектрик поляризуется. Одновременно во внешней цепи по проводникам,

соединяющим обкладки с источником электроэнергии, будет проходить зарядный ток. Изменение зарядного тока в общем случае показано на рис. 3.

При включении напряжения зарядный ток io имеет наибольшее значение. Затем ток быстро спадает и достигает установившегося значения, равного току утечки iyT-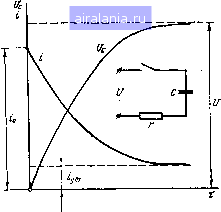

Рис. 3. Заряд конденсатора в цепи постоянного тока

Для идеального конденсатора (tyT = 0) начальное значение тока определяется сопротивлением только внешней цепи: io-U/r.

Значение спадающего тока в любой промежуток вре-

мени может быть определено как i-toe

где е - основание натуральных логарифмов (е=2,72); т - время от момента включения, с; гС - постоянная времени заряда конденсатора, с.

По мере накопления зарядов на обкладках конденсатора напряжение Uc на конденсаторе будет возрастать, приближаясь к напряжению U на зажимах источника. Возрастание напряжения показано на рис. 3 кривой Uc, а величина его в любой промежуток времени Может быть определена по формуле

Заряд конденсатора связан с накоплением в нем электрической энергии, Дж (или Вт-с), 1Г=СС/2/2, где С -емкость, Ф; - напряжение, В.

Если конденсатор, заряженный до напряжения U, замкнуть на сопротивление г, то по сопротивлению пойдет ток. Энергия, запасаемая в электрическом поле конденсатора, будет расходоваться на нагрев сопротивления. Конденсатор в данном случае является источником энергии.

По мере расходования энергии напряжение U на выводах конденсатора снижается в соответствии с зависимостью

Ucui".

Начальное значение разрядного тока ia=U/r.

При дальнейшем разряде конденсатора характер спадания тока будет аналогичен характеру спадания напряжения и с- Разряд конденсатора широко используется в технике для получения кратковременных больших разрядных токов.

Если конденсатор, заряженный до напряжения U, оставить разомкнутым, с течением времени напряжение будет снижаться в результате саморазряда, обусловленного токами утечки. Разрядным сопротивлением в этом случае служит сопротивление изоляции 7?из конденсатора. В процессе саморазряда скорость снижения напряжения на выводах конденсатора определяется постоянной времени конденсатора НшзС

Uc=Ue

Если х=ЯизС, то Uc=Ue-0,37U, т. е. постоянная времени конденсатора численно выражается количеством секунд, необходимых для того, чтобы напряжение на выводах конденсатора в процессе саморазряда упало до 37% начального значения, или это то время, в течение которого конденсатор разрядился бы (зарядился) полностью, если бы при его разряде (заряде) разрядный (зарядный) ток оставался равным начальному значению. Процесс разряда или заряда можно считать закончившимся спустя время, равное трем постоянным времени.

В современных конденсаторах постоянная времени может достигать нескольких суток, что позволяет ис-

пользовать конденсаторы в ряде областей новой техники (в электрических дозиметрах для измерения интенсивности радиации и др.).

Конденсаторы с замедленной поляризацией (с абсорбцией) при кратковременном замыкании на малое сопротивление («накоротко») разряжаются и напряжение на их обкладках спадает до нуля. Однако после размыкания обкладок напряжение может снова возрасти до заметной величины вследствие накопления на обкладках остаточного заряда, что объясняется относительно медленным перемещением зарядов в толще диэлектрика, т. е. замедленной деполяризацией. Остаточное напряжение составляет незначительную часть зарядного напряжения, но в конденсаторах с высоким рабочим напряжением может представлять опасность для обслуживающего персонала. Поэтому такие конденсаторы при разряде должны быть замкнуты «накоротко» длительное время.

§ 7. Конденсаторы в цепи переменного тока

- Из электротехники известно, что если к зажимам активного сопротивления подается переменное синусоидальное напряжение, то протекающий по сопротивлению ток является, как и напряжение, синусоидальным; одновременно с напряжением ток достигает максимальных и минимальных значений и также одновременно меняет знак (направление) при переходе через нулевое значение, т. е. напряжение на концах активного сопротивления и ток, проходящий по цепи, совпадают по фазе.

Действующее значение тока определяется по закону Ома l = Ujr. Среднее значение мощности для цепи, содержащей активное сопротивление, находят по формуле: P=IU=Pr=U/r. Единицей мощности, как и для постоянного тока, является ватт.

Помимо активного сопротивления цепи переменного тока, содержащие индуктивность (катушки трансформаторов, двигателей) и емкость (конденсаторы), обладают реактивным сопротивлением. Сопротивление катушек называется индуктивным сопротивлением цепи или реактивным сопротивлением индуктивности. Сопротивление конденсаторов называется емкостным сопротивлением или реактивным Сопротивлением емкости.

Реактивное сопротивление катушек обусловлено возникновением в них электродвижущей силы (эдс) самоиндукции, которая направлена навстречу приложенному напряжению и создает сопротивление прохождению переменного тока.

Индуктивное сопротивление (Ом) зависит от частоты переменного тока, проходящего в цепи, а также от ! величины индуктивности -и определяется по формуле: ; XL = (,yL = 2nfL, где м = 2я/ - круговая частота, рад/с; L - индуктивность, Гн; / - частота, Гц. 1

Если к зажимам катушки с активным сопротивлением, равным нулю, подается переменное синусоидальное напряжение, протекающий по катушке ток, как и напряжение, является синусоидальным, но отстает от него на 90° (сдвиг по фазе), что обусловлено возникновением эдс самоиндукции. Действующее значение тока, проходящего по катушке, l = U/xL = U/2nfL.

Мгновенное значение мощности для такой цепи определяется произведением мгновенных значений напряжения и тока. Однако среднее значение мощности за период равно нулю. В цепи происходит обмен энергией между генератором и катушкой и энергия не расходуется.

Для количественной оценки интенсивности обмена электрической энергией между источником и реактивной (индуктивной) нагрузкой введено понятие реактив- ной мощности Qi = UI = Pxl = WIxl. Выражая напряжение в вольтах и ток в амперах, получим Ql в вольт-амперах реактивных (вар); реактивная мощность, в 1000 раз большая, называется киловольт-ампером реактивным (квар).

Реактивное сопротивление конденсатора обусловлено появлением на его обкладках напряжения, равного по величине и противоположного по знаку приложенному напряжению. Если к конденсатору приложить переменное синусоидальное напряжение (рис. 4), он будет все время заряжаться и разряжаться, потому что напряжение на его обкладках будет изменяться как по величине, так и по направлению. Вследствие этого в цепи пойдет ток, который будет определяться реактивным емкостным сопротивлением конденсатора (Ом): >:с= 1/юС= 1/2л./С, где С -емкость конденсатора, Ф; / - частота, Гц.

Из приведенного уравнения видно, что сопротивление конденсатора переменному току зависит как от величи-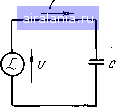

Рнс. 4. Цепь переменного тока, содержащая емкость

ны емкости, так и от частоты тока. С увеличением емкости и частоты тока реактивное сопротивление уменьшается.

Свойство конденсаторов не пропускать постоянный ток и пропускать переменный, а также изменять величину реактивного сопротивления в зависимости от частоты тока широко используется в технике: для разделения постоянной и переменной составляющих напряжения в выпрямителях, разделения токов различной частоты в аппаратуре высокочастотной проводной связи, подавления радиопомех и т. д.

Если конденсатор подключить к сети переменного синусоидального напряжения, в цепи пойдет ток также синусоидальной формы, но будет опережать напряжение сети на 90°.

Таким образом, если в цепи с катушкой напряжение опережает ток на 90°, в цепи с конденсатором оно отстает на 90°. Это важное свойство конденсаторов широко используется для повышения коэффициента мощности промышленных установок, имеющих индуктивную нагрузку.

Изменения напряжений, приложенных к конденсатору, Ис и на обкладках конденсатора ее, тока i и мощности р показаны на рис. 5, а, б. Если напряжение сети увеличивается, конденсатор заряжается (первая четверть периода); ток в цепи имеет то же направление, что и напряжение. Когда напряжение достигнет амплитудного значения, заряд конденсатора прекращается; ток в цепи равен нулю. Во вторую четверть периода напряжение уменьшается и конденсатор начинает разряжаться; ток в цепи меняет направление и т. д.

Действующее значение тока, проходящего в цепи, которая содержит конденсатор, I=U/Xc=2nfCU.

Мгновенное значение мощности для такой цепи определяется произведением мгновенных значений напряжения и тока. Однако среднее значение мощности за Период равно нулю.

В первую и третью четверти периода энергия поступает в цепь от внешнего генератора и накапливается в