

|
|
Главная -> Машинное проектирование 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 [15] 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 высших порядков, возникающих из-за наличия центрального штыря Выражение для тюр ми рока иного реактивного сопротивления тптырей имеет вид {5 25) Поскольку вклад в реактивное сопротивление неодиород ноет и вносят только нечетные типы вoл, то суммирование н этой формуле осущест вляется по нечетным значениям т Диэлектрические штыри. Конструкция и эквивалентная схема диэлектрического штыря в прямоуголыюм волноводе показаны на рис, 5,4<}. Выражения для нормированных реактивных сопротивлений [21 имеют вид {5 26» (5 27) Реактивное сопротивление Ла уменьшается с возрастанием отношения D/a или значения ии проходит через резонансное значение. Реактивное сопротивление Л", также пртходит через резонансное значение. Если D!a - 0,1 а 4 то значение X составляет 3 12 а = О 00093 >32 МЕТАЛЛИЧЕСКИЕ ПОЛОСКИ В ВОЛНОВОДЛХ Продольные металлические полоски. Тонкие, хорошо проводящие полоски в волноводах (рис. S.ba) находят применение в планарных схемах устанавливаемых в Е-плоскости волновода, структурах нэ «плавниковых» линиях, фильтрах и подстроенных мечентах. Здесь будут приведены выражения для различных элементов эквивалентной схемы, полученные вариационным методом {101, Нормированные реактивные сопротивлениях, и определяются X, -Х, + - Х, = ± /> 1 + (5 32) {Ъ .3,3) (5 28) (5 291 Величина S определяется формулой (5 В), Эквивалентная схема, прн веденная на рис 5Ад, действительна для значений длин волн, удовлет воряющих неравенству й < Х-п < 2а а для штыря, расположенного в центре волновода {х - а/2), - неравенству 2а/3 < ?.о < 2а. Точ ность расчета но (5.2(5) (5.29) составляет несколько процентов ,для £)<015аи02< д:,,а < 0.8 при условии, что как Ха, так и Xf, пе слишком близки к резонансным значениям. Резонансы могут возни кать при больших зЕгачениях к„ Для тонких диэлектрических стержней или для малых значений 8г таких, что nOYr 0. эквивалентная схема сокращается до одного параллельного элемента а выражение для реактивного сопро тнвлеиия этого параллельного элемента [[ринимает вид X»- I csce (5 30) Соответствующая реактивная проводимость определяется фopмv.oй ig j%inie (531) Я = 0/(0= f №) Q= B/(P+fl) р 2LtH + A) tp ~ 2+;,(h -A) Л-Ц-е -"-j/t,. (5.34) (5 35) (6 36) (5 37) (5 38) p - коэффициент отражения. Металлическая полоска может не достигать противоположной стенки волновода если<А или соприкасать ся с ней, если d Ь. Значение L различно для каждого из этих случаев 1 Случай d <Ь . В этом случае константа L определяется форму (5 39) (5.40) а Iff (5411 --1 + -*»!" - 2 Случаи d 6 В этом пучае иоистаита L определяется формулой - [ , v.»s,„M) L Jir (5 44) (6 45) Подставив выражения для Р и I? в формулы (6.32) и (5.33 ) полу чим четыре набора значений реактивных сопротивлений Х, и Х,, Два набора дают сопряженные значения проводимостей У и поэтому должны быть отброшены Еще один набор, для которого не выполняет ся условие dX/dm > 0. отбрасывается,поскольку эквивалентная схема не содержит потерь 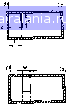 ». г Рис. 5.5. Реактивные металлические эквивалентные схемы: а - продольная-, б - уэкай поперечная
i прямоугольном волновоте В статье j lOI приведены численные значения реактивных сопротиа-снни Xi и в функции ширины металлической полоски W для раз-тчиых значений Хц при d = 7617 мм. При возрастании значений W и л, реактивное сопротивление Xj уменьшается, а реактивное сопротиа-.1еине Xj увеличивается. Для волновода 3-см диапазона прн - 2,5 см ii Xi = 0/2 Аа уменьшается от 1,4 до О 6 при возрастании значения U от О до 5 мм Реактивное сопротивление в этом случае возрастает от О до 0.60 В случае центральной металлической полоски, не сопри касающейся с противоположной стенкой волновода, соответствующие значения Х, и Х изменяются от 0,70 до 0,05 и от О до 0,6 соответствен но. Теоретические результаты для входной реактивной проводимости очень точно совпадают с экспериментальными значениями для полоски шириной 1,777 мм установленной в волновод 3 см-диапазона Измерения проводились в диапазоне частот 8-12 ГГц (10 В предыдущих рассуждениях предполагалось, что металлическая полоска узкая (W Х„) и имеет бесконечно малую толщину. Рас пределенне тока в ней описывается формулой [у) sin (y-b+ d)\ {5 46а) Более точное выражение имеет вид JW ?)--sin[fe„((/-fe + d)]c-v. 5.466) Однако в 3-см диапазоне частот для [Г 5 мм {т е W/J-o < 0,2) гре небрежение изменением тока по оси г не приводит к существенным ошибкам Узкие поперечные металлические полоски. Конструкция, показан ная на рис. 5.56. в работе [11] исследовалась вариационным методом При этом предполагалось следующее распределение тока в металлической полоске: (y-b+d \ »(у) (5 47) Нормированная реактивная проводимость рассмс)Триваемой неодно родности определяется формулой 1(4ш=<1-1.<)= (*,--т-л"/»Ч (5 48) (5 49) (5 50) Vnn определяется формулой (5.42) Уравнение (5.48) применимо на частотах ниже критической. Теоретические результаты хорошо совпадают с эксперимечтальными, полученными в 3 см-диапазоне часгст для W <. .3,96 мм н d< 7,79 мм [И]. Параллельная реактивная прсволи-мость возрастает прн уличенни ширины металлической полоски W и глубины ее погружения d и проходит через резонансное значение при увеличении частоты или глубины погружения. Для металлической полоски, расположенной в центре волноводов, в 3-см диапазоне частот прн d - 5 078 MN значение реактивной проводимости В возрастает от О 50 до 1 50 при возрастании W от О до 7 617 мм на частоте 11 ГГц ДИАФРАГМЫ ИЛИ ОКНА В BOЛПOBOДX [9] Индуктивная диафрагма нли индуктивние окно. На рнс. 5.6а по казан прямоугольный волновод с диафрагмой, образованной двумя пластинами с длинами и {а - d,), расположенными вдоль линий электрического поля. Ширина окна определяется длинами пластин: d-d,d,. (551) Местоположение зкна можно определить следующим образом Xn=-(d, -з)2. (5.52) Для определения эквивалентной схемы используется метод соглашва-ння 19J- Нормированная реактивная проводимость В онределнется формулой I --- Ие* 4 s-(1 (5 54) б • ,5 54) с rcjcos\) (5 55) s-5in()5injj (55Ь( Ноли диафрагма симметричнии (х,, - а,2). го с -.-О, as sm iid/ {2а)\ В этом случае выражение для 5 преобразуется к виду --1-- 36,56,- 1-е, 5" 12s- -l + a,s*(.-2)- (1 .6.>>)(l-e,s»)-l5i«e,(l (5 57) Рнс, 5,6, Пссдчоролности в прямоугольном а - индунтн..!.. диафрагм, или dk.o, 6 - cund * эквивалентнив 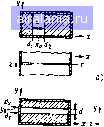 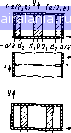 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 [15] 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 0.0088 | ||||||||||||||||