приближенное значение В можно голучить полагая в уравнении (5 57) 6 О В этом случае

l 1 L

(1 -sJ

в 12/ Приведены грэфики отношения Ви/Хд, построенные при иэме иении отношения d;a в пределах от 0.5 до i для значений alX 0,5,. .-,i,3 Для этих значений параметров отношение Ва/Х нзмеинется от 0,96 до О Влияние конечной толщины окна также ИсследоваГО ь сгатье 2f-

Емкостиая диафрагма или емкостное окно. Емкостное окн!1 обра з>ется с помощью диафрагм, края h<mipmx распо.-1ожены периенди кулярно линиям электрического [юля На рнс. 5 66 показзна аснммет ричная емкостная диафрагма Параметры окна связаны с параметрами диафрагмы следующими формулами

d -d, -d,. {0.59)

0 (d, Л) 2 (5 60)

Нормированная реактивная проводимосм!. В эквивалентной схемы он редетнется формулой (9!

В 1п5-

казона длин волн, но не превышает 5 %. Погрешность уравнения {5.64) не 1тревыцает 5 %, если b<iX„, и не превышает 1 %, если Ь -< Xj2 Отношение BXJb может быть [1айлено по графикам, приведенным в 121 чля значений d/b - 0...1 и ЫХ„ 0. . 1 отношение изменяется от О бдо О [[ри изменении dlbai 0.15 до 1,0.

Влияние конечной толщины симметричного окна также исследова но в 121. В этом случае эквивалентная схема представляет собой П-об разную схему

Емкостные металлические полоски !9 Емкостная .четал 1ическая гюлоека (рис 5,6в) является эквивалентом емкостного окна.

Выражение для нормированной реактивной проводимости Во в слу чае симметричной емкостной металлической полоски совпадают с вы ражением проводимости для симметричной диафрагмы (5.64). В этом случае d, как и ранее, означает суммарный размер отверстии а не ширн})у металлической 1к>лоски, т е. d d, + (fr - d).

Для симметричной емкосгной металлической полоски

в(Р)

В = 1п ,

?в i (1 i s)e(0) I

(5 бй)

где в (р) - тета-функ[шя Якоби Значение отно[иення в ф) в (0) л жет быть рассчитано ио формуле

[2»

Д1Я симыетричиого окна код;

I 21ns --

Ь 2 имеем

(б 62) (.>.6.3)

S-- b\n\j\d,{2b)\, с а,5л<г,(26);

Эквивалентная схема, показанная иа рис. э бб справедтива при Ь<; XJ2 для асимметричной диафрагмы и при b<iX для симмегрич пой диафрагмы Погрепгность (5.61) во.чрастает на нижнем котше аиа

(5 Ы)

10.65) (5.66)

(67)

Значение & определяется из уравнения сп - с {\ - s), где сп глиптическая функция Якоби. Модули полных эллиптических hi тегралов К и К определнютсн формулами

а(7 = ехр1 -лК. (ft)/Л" (А)). Пирометры (-и s определяются формулами (5.62) и (5.63) соответственно.

Комбинации диафрагм и металлических подосок 191- На рис. 5 6г показана симметричная индуктивная диафрагма в сочетании с цент ральной индуктивной металлической полоской. Эту конфигурацию можно также назвать двойным симметричным окном Реактивное со противление X определяется формулой

О 69)

где £ и /с - полные эллиптические интегралы е модулем k определяемым (}"Р"У-ой

* [,-si,.(„,..(i)]

Прн d, О фopмvлd (5.69) преобразуется в формулу реактивного сопротивления симметричной индуктивной диафрагмы, а при а/2-одиночной нейтральной металлической полоски. Две симметричные индуктивные металлические полоски (рис. 5.6rf). Выражение для реактивного сопротнвтения может быть найдено, как

X -I h

(5 70)

где модуль к пол-ых эпиптических интегралов Е и К опреде1яется по формуле

h sin {ldt/u).( (idyO).

При d, О формула (5.70) иреобразуепся в формулу реактивного со противления симметричной индуктивной диафрагмы показанной на рис. 5.6а

S34 ступгпьки b вoкm(дAx

Ступенька в Н-плоснт:ти или скачок по ширине волновода I2J

Геометрии симметричного скачка по ширине прямоугольного волново да показана на рнс. 5.7о а неоднородность, образукяцанся на стыке двух прямоугольных вожоводоо. называется ступенькой нли скачком в Н-пло(гкостн. В анализе предполагается, что в каждом волноводе рас-нросграняетсн только основной тип волны Все высшие типы члн затухают. Выражении для нормированных реактивных сопротивлений неоднородности стыка со стороны волноводов большего и меньшего сечений в плоскостях Т и Т соответственно определякэтся формулами

(э71)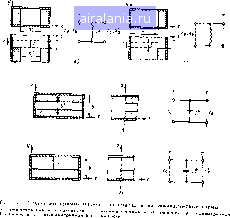

Константы Л,., и Л„нвляюся элементами матрицы сопротив пении Т-четырехполюсника в общей тоскостн отсчета Г и оппвделя ются формулами Недели

-((Л - (J=.V,, . 2(Л i ICV„ ; С--Л,,{

1/а -.

С1Х„,л

(5.72) (5 73)

где / 2а Х

2а ,К

д 1 »,)Г1 К,, 1-Г {14Я,)(-К,, л

(1 + Я,)(1-Я,) 7- (,TTJ

Af„--9ejl -[Е(а) aK(tt)\\E(a) К (а )l

-д;-аТ+ ад!(0-е) + 4к;0 -в)

I а

Л„-9вТа"-*

!-£foc )-а/СС» )\ + R -aRj i

+ \-R,R,[aRUQ-0) + Rifi -в )l

функции /с (a) и £ (a) есть полные этпиптические интеграпы первого и второго рода соответственно.

Значения параметров эквивалентной схемы полученные из при веденных здесь уравнений, справедливы в области 0,5 <: «Д„ < < 1,5 и 2а > Хо. В большей части этой области точность уравнений лучше 1 % На границе области при а/К .5 точность ухудшается до 5 %.

Несимметричный случай. Несимметричное изменение ширины вол повода показано на рис, 5.76. Выражения для Zo/Zo, A/Zo и 1/а. полученные для симметричного случая, могут использоваться и для этой конфигурации но входяп1,ие в них константы определяются иначе

1 -i- За*

-R -Ri-

-2 32а

Q l 2e. 1- 2H

2ft-{uД<,) 2H

ЗквНБэлеПтная схема справедпива при 0.5 <; wX <. I ,С, Приведенные формулы, определяющие значения параметров эквивалентной схемы, имеют точность окою ! % в большей части чшй области. На границе области при й/л - 1 О погреппюсть может достигать 5 %.

Графики значений отношения X%J(2a} в зависимости ст величины а. значение которой изменяется а пределах от 0.2 до 1 прн Ха - 1,05 и 2, приведены в работе [2. Эти графики дают 6ojiee тчные значения, чем приведенные здесь выражения имеющие замкнутую срорму. Значение отношения XXJ(2a) возрастает от О до 6 при юзрастании а от 0,2 до 0,8 (при Х„/а 1,05). Отношение Оа увеличивается от О до 1,04 10" при изменении значения а от О до 0,5, Вблизи а 05 кривая симметрична,

Ступенька в Е-плоскости или скачок по высоте прямоугольного волнсйюда [2), Для ступеньки в Е-плоскости, показанной на рис. 5.7б, .значение нормированной реактивной проводимости сгыки можег бык найдено из следующих выражений

а (5 74)

1 2я

-1п(г)+2 -

.4 А

(5 75)

. Vi-p 1 yrrj.