Индуктивность прямоугольной полоски в свободном пространстве, удаленной от других проводников и магнитных материалов определяется как [5]

10 и{\п

- + 1 193 Ю 2235 j

(7 8)

где Z,/ - в наногенри а все размеры - в миллиметрах

Зависимость от частоты к влияние заземленной пластины На

высоких частотах значение индуктивности уменьшается из-за скин эффекта Уменьшение индуктивности составляет около 4 % на частоте 1 кГц, а с дальнейшим ростом частоты это значение остается неЕ)змениым 6. Наличие заземленной пластины также оказывает влияние на зла чение индуктивности: при приближении заземленной пластины индук тивиость уменьшается Гб] Это уменьшение может быть учтено с по мощью корректирующего коэффициента J(g. С учетом коррекции эф фективная индуктивность 1.ф может быть записана в виде

1фф -K,L (7 9)

где Lh ~ значение индуктивности в свободном пространстве. Умснь шение индуктивности было измерено !7] Результаты измерений могут быть записаны в замкнутой форме

/(,-0.57-0 U51n(ir i) (7,10)

где W - ширина ленты; Л - ее расстояние от заземленной пластины Ненагруженная добротность Q полоскового индуктивного элемента может быть найдена по формуле

Для медной полоски {R, 2 61 Q -4,81 10/ i-K

(7 11)

/ ) и для W/t 10 имеем (7 12)

Как ВИД1Ю из (7.12). для индуктивностей более 1 нГн значения доброт-ностей Q :> 100 на частоте около 1 ГГи могут быть получены при широких полосках il/W < 15). Эта формула справедлива, если толщина / Существенно превышает двойную глубину скин-слоя,

Полосковые индуктивные элементы практически могут быть выпол иены для значений индуктивностей не более 2 нГн. Длина индуктив ного элемента при чтом составляет около 2,8 мм (при - 10). Эта длима меньше одного витка спирали диаметром 1 мм Для больших индуктивностей необходима многовитковая спираль для которой фор Мула (7,12) несправедлива.

Спиральные индуктивные элементы, Конфигурация плоской спи ральной полосковой катушю; индуктивности показана на рис 7-)о. Формула индуктивности для спиральной катушки содержащей п витков, может быть записана в виде [5. 8, 9]

1,- 0.3939тп=й(1п-- 1(У(1п 3 583)-} (7 13)

w. 7 1 Ковфнгура ия спиральной ка-I шкн индуктивности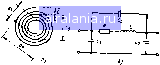

где/, - - внаногенри; « . (d„ + d,)/4 (т. е. средний радиус); С (d- - d,)2; d, Hd„ - минимальный и максимальный диаметры (в мнллимет pax) соответственно. В работе 110] приведена простая аппроксимация которая в большей части диапазона дает численные значения индуктив иости (нГн) с погрешностью, не превышающей нескольких процентов по сравнению с формулой (7 13):

-39,39/iV(8fl . lie)

(7 14)

1Де все размеры в миллиметрах. Измерения показали что фактические значения индуктивностей отличаются не ботее чем на 20 % от теорети чески рассчитанных значений 115].

Сопротивление спиральной катушки индуктивности может быть рас счнта1ю как

R К -i naR W

(7 15)

где Л" --корректирующий коэффициент, аналогичный коэффициенту К для прямой ленты и учитывающий заполнение током. Из (7.14) и (7 15) может быть найдена добротность плоской спиральной катушки

7.877 - 10-е/Гли

KR, (8(j j 1 Ic)

(7 16)

де a, v н W задаются в миллиметрах. Эквивалентная схема спиральной катушки индуктивности содержит не только индуктивность. В нее входят и паразитные элементы, такие как собственная и межвитковая ем кость С„ и параллельные краевые емкости Cj и возникающие из-за влияния заземленной пластины [4], Эквивалентная схема спиральной катушки индуктивности с учетом паразитных элементов показана на рис, 7.16 Последовательное сопротивление R учитывает потери. Для спирали диаметром от 1,0 до 5 мм на подложке из окиси алюминия ти пнчные значения паразитных элементов имеют следующие значения Со 0.15 пФ. С, = 0,1.. 0.2 пФ. С, О 05.,.0.1 пФ. а добротность на частоте 4 ГГц 80 ,.100. Эмпирическое соотношение для емкости С„ (пФ) может быть записано в виде (4:

Со -0.035d,i 0 06 где d„ - внешний диаметр спирали мм

(7 17)

Некоторые основные положения используемые при коиструиро вании катушек индуктивности, могут быть сведены к следующим:

1. Лента спирали должна быть по возможности более широкой (большое значение U) и в то же время внешний диаметр {d„) должен сохраниться небольшим. Это означает что межвитковые расстояния должны быть предельно малыми.

2. Должно быть некоторое пространство в центре спирали катушки через которое силовые линии будут проходить насквозь, в результате чего возрастает запасенная энергия на единицу длины. Из I9J следует что нри dj/de достигается оптимальное значение добротности.

3. Поверхностное сопротивление возрастает по закону Следовательно, добротность катушки должна возрастать по закону корня квадратного из частоты. Однако экспериментально обнаружено что добротность возрастает только до опредеченной частоты, а затем быстро уменьшается П.171. Вероятно, это происходит из-за того, что катушка начинает излучать высокочастотную энергию. Измерения доб ротности показали, что при К 1 ее значение составляет до 2/3 от теоретического значения. Выбор значения К 1,5 дает разумное при ближение формулы (7.16) к экспериментазьиым данным Значение добротности может достигать 100

4 Показано, что Д-1я одного и того же размера d„ добротность круглой спирали выше, чем прямоугольной (примерно на 10 %), хотя индуктивность существенно меньше (примерно на 20 %).

5. Многовитковые катушки характеризуются высокими значениями добротности (из-за высокой индуктивности на единицу площади), но из-за натичия межвитковой емкости частота их собственного резонанса ниже, С ростом диэлектрической [юстоянной подложки межвитковая емкость возрастает и частота собственного резонанса уменьшается Это приводит к возрастанию реактивного сопротивления катушки

Проволочный индуктивный элемент. В качестве проволочного индуктивного элемента в СВЧ интегральных микросхемах используется контактная проволока, служащая для соединения с активными элементами и другими крупными компонентами. Индуктивность (нГн) провода диаметром d в свсдном пространстве определяется форму лой [5]

и 02;[ln(4/d)-l (718)

где / и d - в миллиметрах

Сопротивление проволоки дтннои I рассчитывается но формуле RRJ/{nd). (7 19)

а добротность опредетяется как

Q-2:fU-R (7 20)

Сравнивая выражение (7.20) с аналогичной формулой для гюлосковых катущек, находим, что для значений d, совпадающих с шириной ленты W, проволочный индуктивный элемент характеризуется более высокой добротностью. Это объясняется тем, что площадь поверхности (для тока) у проволоки больше чем у полоски 130

Влияние заземленной пластины на значение индуктивности прово 10ки также исследовано [5]. Если проволока находится на расстоянии от заземленной тастины то индуктивность (нГн)

02/ in !п

1 - ур \и-

V V 4Р I 21]

(7 21)

в миллиметрах

;22 конденсаторы

Конденсатором с сосредоточенными параметрами является разомк [!утая линия небольшой длины (рис 7.2а). Входное сопротивление такой линии может быть записано в виде

Рели у1 \ то (7 22) может быть представлена в виде

(7 22)

j,.,c7

Отсюда видно, что эквивалентная схема содержит активное сопротивление giiaCH), соединенное (юследовательно с конденсатором емкостью С{ Аппроксимация второго порядка (в пренебрежении L) дает

i и>С1

17 241

Формуле (7 24) соответствует последовательная схема с двумя рези стерами и конденсатором, как ггоказано на рнс. 7.26. Второй член определяет последовательное сопротивление учитывающее потери проводимости. Его можно записать в виде

г/ 3=2/, /.(3W)

(7 25)

1де г = 2R„iW. Следует заметить, что только внутренняя сторона по верхности шириной W вносит вклад в потери проводников, а коэффициент 2 учитывает,что потери возникают на двух пластинах конденсатора Другая составляющая сопротивления /{а>(У1) определяется потерями в диэлектрике и может быть рассчитана ио формуле \ {QmCI).

.нутан jiH-

денсатора (о) и его Iff)

Рнс 73 Конфигурации плоского к01Ыенсатор<1 и его эквивалент оя схе

чэ (6)

где - добротность диэлектрика, равная (лС>д. Суммарное значение добротности может быть найдено из уравнения

1/Q = l/Qnp + 1 С?-, (7 26)

[ де добротность проводников рассчитывается по форму le

Q„={1 i,iClj(3Wf2R I] (7 27)

Добротность квадратного конденсатора {W - /) с медными обкладками имеющего суммарную емкость Се (пФ) может быть рассчитана по формуле

Q„. = 29 IlWC) (728)

где / - в гигагерцах

Для получения больших значений емкости на единицу площади необходимо уменьшать расстояние между двумя проводниками (верх него и нижнего) отрезка линии передачи, С тех пор как обычные значе ння толщин подложек из окиси алюминия достигли примерно 0,6 мм, появилась возможность изготовления конденсаторов больших емко стей с использованием структуры металл диэлектрик - металл иа верхней стороне подложки. Конфигурация такого конденсатора показана на рис. 7 3а Толщина диэлектрика {обычно двуокиси кремния), используемого для этой слоистой конфигурации, обычно составляет 0,5-1 мкм. Этот тип конденсатора изготавливается на диэлектрике с добротностью на / I ГГц около 600 С ростом частоты значение доб ротности снижается в соответствии с формулой (7.28).

Для увеличения точности расчета емкости многослойных конденса торов необходимо учитывать влияние краевого поля.Этот расчет был приведен в статье ПП. В этой работе прямоугольный конденсатор рассматривается как линия длиной / н шириной W Емкость рассчитывается по формуле

. 1 2С„ 4- 2С

(7 29)

дс Се, и - краевые емкости определяемые формулами С, =J f ! IF ] ,

2 ( viZ,( h м /

C„, = J-f \ "rl

2 i t,, Z, (

(7 30) (7 31)

li этих уравнениях у, н - фазовые скорости, а 2, и Z, - волновые опротивлення микрополосковых линий сширинами W и / соответст )енно ч

Для квадратного плоского конденсатора {/ = W) v. = v, » Z, = = Z, Следовательно

2 ] vZ (W h. «г)

(7 32)

Лчя расчета емкости конденсаторов круглой формы определяется эк бивалентная диэлектрическая постоянная в каком-либо направлении как для микрошлосковой линии. Эта эквивалентная диэлектрическая постоянная затем используется для расчета, как и в случае однородной конфигурации При этом предполагается, что краевое поле круглого конденсатора с большим радиусом {/-„/Л > Ю) аналогично краевому 1юлю прямоугольного конденсатора Это предположение дает

--(2е«г„ А)

(7 13)

де Z (2 г,„ Л, е,) волновое сопротивление; v - фазовая скорость для микрополосковой линии шириной «-2 г„. Емкость круглого конден сатора может быть записана в виде [П

1п f 1 7726

(7 34)

Эквивалентная схема плоского конденсатора показана на рис. 7.36 Здесь R - потери конденсатора. Паразитными элементами являются последовательная индуктивность L и краевые емкости на корпус С, и Cj !4. Типичное значение последовательной индуктивности для номи нальных размеров 1 0.5 мм (перекрытие 0,25 мм) составляет 0.5 нГн Значения краевых емкостей С, и С лежат в пределах от 0,05 до 0,2 пФ Имеется и другая конфигурация сосредоточенных конденсаторов малыми значениями емкостей (рис 7,4 а)встречно-штыревая. В таком конденсаторе оба проводника расположены на одной верхней .тороне диэлектрической подложки. Конденсаторы этого типа, если они входят в состав мнкрополоскового узла, изготавливаются в едином тех (юлогическом цикле с этим узлом, и никаких дополнительных опфаций для их изготовления не требуется.

Анализ конденсатора нз встречных штырях описан в статье [12] Гмкость между двумя штырями такой структуры для случая бесконеч