но удаленной заземленной пластины может быть найдена по формуле емкости для нечетного типа возбуждения связанных микрополосковых 1ИНИЙ. Если влиянием заземленной пластины пренебречь нельзя, то необходимо учитывать также вклад четного типа возбуждения. Для рис. 7.4а имеем 112)

C--/{t, 1)[{Л? -3) Л,-ьл21 формула С/(е, + 1)

(7 35)

1де С-в пикофарадах Л? - число штырей; 0.0886 пф/см

Лг --- 0,0993 пФ/см для бесконечной толщины подложки или отсутствия заземленной плоскости; / - в сантиметрах

Добротность встречно штыревого конденсатора определяется как

Qc -l/(wCR„„.,) (7 36)

,7 37)

ах - ширина ячейки, как показано на рис. 7.4а

Как и для конденсатора многослойной структуры добротность определяется потерями в диэлектрике и в проводниках Добротность конденсатора емкостью 2,83 пФ {N - 40, / 1,137 мм, х 0,0508 мм), изготовленного на подложке из окиси алюминия (чистота 99 5 "о) толщиной 0,609 мм по результатам измерений составляет 677 на час тоте I 92 ГГц [12.

Так как .ггиния передачи имеет индуктивный характер то встречно штыревые конденсаторы являются многорезонанснымк устройствами Изменение емкости нри изменении частоты зависит от отношения W/L Оптимальное значение отношения W/1, при котором изменение емкости с частотой минимально, может быть найдено численно. Так например для W/1 - 1.66 и jV 24, значение емкости [юстоянно до частоты 3 ГГц

Встреч но-штыревой конденсатор имеет добротность того же поряд ка что и многослойный конденсзтср и изготавливается непосредствен но на подложке из окиси алюминия без использования дополнительных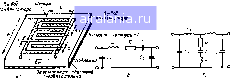

Рис. 7.4 Конфигурация конденсатора на встречных штырях (и) и жнива ные схемы при его последовательном (б) н параллельном {в) включениях

Рис. 7., Резонаторы с сосредоточен ными параметрами.

о - последовательный б параллмьный

111 электрических материалов На :1стотах до 3 ГГц могут быть полу чсны емкости от 0,1 до 10 пФ. Для получения больших значений емко ( 1ей необходимо использовать мно юслойные конденсаторы. Встреч-ио-штыревые конденсаторы зани-\шют ббльшую площадь, чем мно юслойные- Так, например, конден-uiTOp на встречных штырях емкостью 12 пФ имеет размеры 12,7 X 1,78 мм, тогда как много i .юйный конденсатор той же емко

(ги с диэлектриком из SiOj толщиной I мкм имеет размеры 0,559 X 0.559 мм. Тем не менее для малых значении емкостей конден-аторы этого типа предпочтительнее, так как здесь используется только один металлизированный слой.

Эквивалентная схема встречно-штыревого конденсатора с учетом паразитных» элементов показана на рис. 7 4 б в (4[- Последователь ному включению конденсатора соответствует эквивалентная схема на ( ИС. 7.4 6. параллельному - на рис 7.4 в.

Используя комбинации элементов с сосредоточенными индуктив костью и емкостью, можно получить резонаторы с сосредоточенными параметрами. Если используются встречно-штыревые конденсаторы 10 резонатор изготавливается в едином технологическом цикле, Воз-\южны как последовательные, так и параллельные резонаторы, кото )ые используются в устройствах фильтрации 113 14]. Конфигурации резонаторов показаны на рис, 7,5. В [14] показано, что в диапазоне частот от 5 до 10 ГГц может быть изготовлен параллельный резонатор с сосредоточенными параметрами с одновитковой катушкой индуктив 1ЮСТИ, активное сопротивление которой составляет около 1 Ом и менее Это соответствует значению добротности между 10 и 90

Значения индуктивностей, рассчитанных по формулам (7.8), (7.13) (7.18), отличаются от соответствующих измеренных значений не

Гюлее чем на 20 %. Это от/

ичие может возникнуть из-за «паразитных»

емкостей и индуктивностей, из-за неточности приближенных расчет-пых формул в замкнутой форме, а также из-за погрешности измерений. Измеренное значение добротности составляет приблизительно половину от расчетного значения, соответствующего рассчитанным значе-1ШЯМ активных потерь и индуктивности. Существует также разница между измеренными и расчетными значениями добротности конден-i аторов.

Расчетные формулы, дающие погрешность около 20 %, мало прнгод ы для машинного проектирования. Этн формулы могут быть полезны i лучшем случае при первоначальном проектировании. Следовательно, возникает необходимость моделирования элементов с сосредоточенными параметрами на основе измерений. Техника измерений, поз-юляющая получить точные характеристики таких элементов, рассмат ривается в следующем разделе.

7.3, ИЗМЕРЕНИЕ ХАРАКТЕРИСТИК ЭЛЕМЕНТОВ С СОСРЕДОТОЧЕННЫМИ ПАРАМЕТРАМИ

Элементы с сосредоточенными параметрами имеют малые размеры Поэтому для измерения их параметров необходимы специальные ме тоды. Наиболее часто применяются три метода измерения реактивного сопротивления и добротности таких элементов. К ним относятся: I) прямые измерения сопротивлений с помощью измерения коэффициентов отражения. 2) включение элемента с сосредоточенными пара метрами в резонансную структуру с тем, чтобы полученные изменения давали информацию об этом элементе и 3) изучение реактивной прово димости соединения элементов с сосредоточенными индуктивностью и емкостью вблизи резонанса.

Прямые измерения сопротивления элемента с сосредоточенными параметрами могут производиться на измерительных линиях, реф лектометрах и измерителях полных сопротивлений. Использование измерительных 1иний обеспечивает точные результаты только до 2 5 ГГц. Измерение добротности и реактивных сопротивлении на более высоких частотах становится затруднительным из-за того, что потери в линии становятся соизмеримыми с потерямн в активном сопротив лении элемента Подфобное описание прямых измерений сопротивле НИИ приведено в [15].

Резонансный метод для элементов с сосредоточенными параметрами может использоваться до 12 ГГц, Этот метод основан на измерении частоты резонанса и добротности резонансной линии [1ередачи

При включении элемента с сосредоточенными параметрами в линию изменяется резонансная частота и добротность, и по этим изменениям может быть найдено сопротивление элемента. Так как линия передачи резонирует на многих собственных частотах полное сопро тивление элемента может быть найдено по изменению частот.

Рассмотрим линию разомкнутую на одном конце и нагруженную на элемент с сосредоточенными параметрами - на другом, как пока зано на рис 7,6. -Эта линия будет резонировать когда

lXjZoCtg6 (7,38)

где X - реактивная составляющая сопротивления элемента 8 - электрическая длина линии передачи определяемая по формуле

b-2nniv, (7.39)

НУ- резонансная частота, длина линии и скорость распростране ния волны соответственно. При отсутствии элемента с сосредоточен ными параметрами эта линия передачи резонирует при выполнении следующего условия-

nn---2nj„ l.v, (7 40)

где /„ - резонансная частота п го порядка Из (7.39) и (7 40) можно определить в в зависимости от двух значений резонансов

е = «п /„ (7 41)

Следовательно из (7 38) и.меем x Z,ctg(«n „)

(7,42)

где / - резонансная частота линии, нагру ..............-

женной на элемент с сосредоточенными па раметрамн (рис. 7.6), а - резонансная Рнс 76 Линия передачи частота той же 1ИННИ разомкнутой с нагруженная на элемент с обоих концов с,.1-ре.1эточенными парамет

Нрам» на одном конце и ра а практике первоначально измеряет зочкнутая »а другом ся значение частоты {„. Затем в линию конце устанавливается исследуемый элемент и из

меряется резонансная частота /, Измерения могут производиться и с помощью двух идентичных линий, изготовленных на одной подложке. В одну из них устанавливается исследуемый элемент, В этой системе измеряются кратные резонансные частоты каждой линии и затем определяются значения реактивного сопротивления для ряда ли скретных значений частот

Добротность элемента с сосредоточенными параметрами может быть рассчитана по измеренным значениям добротности непагруженной линии и линии, нагруженной на исследуемый элемент. Поскольку суммарная энергия потерь равна сумме э[[ергии потерь в линии и элементе то можно записать

(7 43)

где ua и ui - значения энергии запасенных во всей системе, в ненагружепиой линии и исследуемом элементе соответственно; Q, Qo н Qi-Соответствующие значения добротностей. Значение uai равно сумме u. Значения Qi н измеряются, Значения энергий u-i и рассчитываются по Приведенным здесь формулам Энергия, запасенная в линии передачи,

tfl =j [/„ мп {jrHd -ljll./g(2H- <тщ11А

(7 44)

де Ln - погонная индуктивность линии; 8 ~~ электрическая длина линии, определяемая формулой (7.39). Энергия, запасенная в элементе с сосредоточенными параметрами, может быть найдена по значению протекающего через него тока. Для индуктивного элемента запасенная энергия определяется как

t/, L (/„ sin 0)/2 ЦВ

Теперь из (7.43) - (7 45) может быть найдена добротность

/.4ч в А \ q, >

(7 45)

(7 46)

\йс А и В определяются формулами (7 44) и (7 45)

соответственно.

Точность Этого метода измереннГг возрастает с ростом разности (Ui/Q,- iUQn)- Поэтому для увеличения точности значение доброт ности линии передачи Qo и отношение энергии, запасенной в элементе к энергии линии UjUo, должны быть как можно большими Отношение UJUa зависит от волнового сопротивления линии.

Для этих измерений используются резонаторы на коаксиальных микрополосковых и копланарных линиях.

Если использовать полуволновый резонатор, го элемент с сосре доточенными параметрами можно включить в центральном сечении ре зонатора последовательно, как показано на рис. 7.7. Такой способ включения элемента с сосредоточенными параметрами приводит к из менению резонансной частоты для таких типов колебаний в резонаторе для которых в сечении элемента ток имеет ненулевое значение. Основ ной тип колебаний в резонаторе и нечетные гармоники обладают этим свойстюм, При последовательном включении элемента в центральном сечении линии формула (7,42) остается справедливой при замене / на fl2, а Zf, на 2 Z. Возможно также параллельное включение элемента с сосредоточенными параметрами в центральном сечении линии передачи, образующей резонатор. В этом случае включение элемента будет оказывать влияние только на четные гармоники основного типа колеба НИИ, и в формуле (7.42) необходимо заменить / на 2, а Zo на Zo/2

В работе 1161 показано, что характеристики элементов с сосредого ченными параметрами могут быть найдены путем исследования реактив ной проводимости лизи резонанса параллельного резонансного кон тура, состоящего из катушки и конденсатора с сосредоточенными пара метрами. Измерение реактивной проводимости и КСВН вблизи резо нансз позволяет полностью определить:

а) значение производной с(В/с(м = 2С при резонансе; б) резонанс ную частоту и, следовательно, по известному значению емкости С ин дуктивность L: в) проводимость G - по значению КСВН при резонан се и затем рассчитать добротность по формуле

(7 471

Значения добротностей отдельных элементов определяются не просто.

Для измерений может быть использован параллельный резонансный контур показанный на рис. 7 8. изготовленный на кварцевом дис-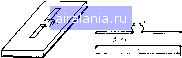

Рис. 7.7. Последовательное включение элемента с сосредоточенными пзрам< ми в центральное сечение резонатора

не толщиной О 5 мм Этот контур включается параллельно в коаьсиаль ную линию, нагруженную на коаксиальный волновод вблизи крити ческой частоты, создающий условия холостого хода Коаксиальная шнпя с испытательным приспособлением поча.1ана на рнс. 7.Q

Глава 8

ДВУМЕРНЫЕ ПЛАНАРНЫЕ КОМПОНЕНТЫ

Ра.злич!1ые типы компонентов СВЧ устройств рассмотренных в предыдущих главах, могут быть разделены на три группы. Элементы с сосредоточенными [[араметрами. рассмотренные в гл. 7 могут быть названы нульмерными Э1ементамн. так как их размеры по всем трем координатам намного меньше длины волны К соответствующей рабочей частоте. Линии передачи (коаксиальные, полосковые. микрополоско вые и копланарные), рассмотренные в гл. 3, могут быть отнесены к одномерным элементам, так как размеры их поперечного сечения нам ного меньше длины волны а длина соизмерима с длиной волны Раз меры поперечного сечения волноводов, рассмотренных в разд. 3.2 также сравнимы с длиной волны и. следовательно, используя аналогич ную терминологию, их можно назвать трехмерными компонентами Кроме того, имеются компоненты, один нз размеров (высота) которых намного меньше длины волны, а два других - сравнимы с длиной волны или превышают ее Эти компоненты, называемые двумерными планарнымн компонентами, рассматриваются в настоящей главе.

Возможны три конфигурации планарных цепей. К ним относятся

1) грех плоскостные, или полосковые (рис. 8.1а, в)

2) открытые, или микрополосковые (рис. ЬЛб в)-

3) волноводные (рис 8.1г).

Понятие двумерных планарных цепей используется в СВЧ интег ральных микросхемах волноводных узлах, ферритовых элементах и