Двумерные СВЧ

микрополосковых антеннах. HeKorophif .кктоинства танарною пред ставления ценен состоят в следующем-

А. Одномерные цепи на полосковых и микрополосковых линиях могут рассматриваться как частный случаи двумерных цепей. В ин тегральных микросхемах СВЧ фактические длины линий на высоких частотах уменьшаются, а ндирнна линии увеличивается для обеспечения малых значений волновых сопротивлений (в которых обычно размещаются СВЧ i юлу проводниковые приборы) В этих случаях планар-ное представление цепей дает более точные характеристики интегральных микросхем, чем приближение с помощью линий передачи.

Б. Планарное представление цепей может быть использовано также для анализа неоднородностей в гюлосковых и микрополосковых ли ниях. Оптимизируя конфигурацию неоднородностей, их влияние мож ио скомпенсировать Это позволяет улучшить характеристики ], стройств.

В Использование планарного представления цепей позволяет по лучить некоторые новые конструкции. Например, как показано в 111, дисковый резонатор может использоваться в качестве трехдеешбель-ного ответаителя

Г Планарные узлы изготовленные на ферритовых поД)10жках. также могут исследоваться методом планарного приближения, а технические приемы, используемые Для анализа устройств на диэлектрических подложках, расширяются. Этим метком можно оптимизировать топологию широкополосных циркуляторов [2].

Д. В микрополосковых антеннах распределение поля можно оценить, рассматривая их как планарные компоненты с магнитной стенкой. Планарное приближение может использоваться для оценки поля по периферии этих компонентов.

Е. Прн использовании техники фототрзвления тготовление пла парных узлов проще, чем трехмерных волноводных 140

8 1 ОСНОВНЫЕ СООТНОШЕНИЯ {31

Рассмотрим планарную цепь полоскового типа показанную на рис. 8.2, и основные уравнения, позволяющие получить параметры цепей, представленных в виде эквивалентных миогополнхников.

В схеме, показанной на рис. 8.2, центральный проводник имеющий произвольную форму, расположен между двумя заземленными пласти нами, расстояние между которыми составляет 2 d. Эта схема возбуж дается симметрнчрю из-за наличия верхней и нижней заземленных пла стин. На краях центрального проводника имеются несколько выводов Обозначим ширины этих выводов Hf,, Hf и т д Остальные кран цент рально]-о проводника являются разомкнутыми. Выберем направление координатных осей так, чтобы рассматриваемый центральный провод [[ик произвольной формы лежал в плоскости ху, перпендикулярной оси Z- При этом размеры центрального проводника по осям х у будут соиз меримы с длиной волны, а размером по оси г (толщиной) можно лренеб речь. Следовательно поле по направле1шк> оси г можно считать по стоя иным.

Основ1юе уравнение Гельмготьца сгграведтивое Д1я источника в свободной зоне, имеет вид

(W) Е - О

(8 1)

где р и е - магнитная i диэлектрическая прошщаемости материала диэлектрика; о - уг.ювая частота. Это соотношение хорошо описывает поле внутри диэлектрика. Тангенциальные составлякнцие электри ческого поля вблизи центрального проводника и заземленных пластин равны нулю. Предполагается, что на краях двумерного планарного компонента существует магнитная стенка. Поскольку в направлении оси г поле не изменяется, то обе составляющие поля и внутри диэ лектрика равны нулю. Краевое поле на краях планарного компонента можно учесть перемещением магнитной стенки на некоторое расстояние от физического кран центрального проводника. Это перемещение ил люстрнруется на рис. 8.3. Для планарных цепей полоскового типа маг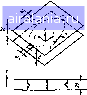

Рис. ЙЗ Перемещение ctthkh для учета краевого

нитные стенки должны Оыть сдвинуты на расстояние 6 определяемое формулой 14]

6 (2d In 2) л (8 2)

Значение fi определяется точно только для полубесконечного пла нзрного компонента, однако онс может быть использовано в большинстве практических случаев Для нейтральных проводников прямоугольной формы значение 6 может быть получено иа основании (6.2) Для узлов микрополоскового типа 15] значение f> на.ходится нз выражения для оконечной краевой емкости микрополоскового проводника (7,31). Необходимо отметить, что векторы полей под центральным проводником п т!ад ним должны быть направлены противоположно. В дальнейшем анализе векторы Е и Н 0(трсде,(яются по напряженности ноля с одной стороны центрального проводника (например, с нижней)

Поскольку составляющие £, и £у равны нулю, этектрическое по le двумерных ком1гоне(ггов может быть записано в виде

Е а Е {x у)

(8 3)

где а - единич.,ыи вектор, направленный вдоль оси га -Щз пол«£ является функцией только координат .t и у Подставтяя (8 3) в (8 1) и полагая дЕ, дг-- О, получаем

где Vt - Лй<М ddii

Ис„о.,ь.-,уя ур.-,ш,еш.е Максве.пла ма.нит.юе по,е мож,ю записать в виде Н- -

(8 5)

и ти с учетом (8 3)

(В Ь)

где а„ а,- единичные векторы направтенные вдоль осей х и у со °п™рхностный ток нентратьного проводника может быгь получен из граничных условий

J, п X (Н,-Н )

(8 7)

гпе п единичный вектор, направленный нормально к границе Н н" - напряженности магнитные по.тей с двух сторон вентрального прош1ника Для центрального проводника двумерной цепи l.oлocкoвo-та н; - Н„ следовательно j, (А/м) определяется как

дЕ, , дЕ, \ (8 8)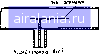

В планарных цепях микрополос Щмр*

кового типа выше верхней плоскости центрального проводника магнитное поле отсутствует и поэтому в фор муле (8.8) для получения поверх постного тока центрального провод ника коэффициент 2 должен быть опущен.

Выражение для поверхностного тока (8-8) имеет силу для всех то чек двумерного центрального про """" водника произвольной формы вклю

чая его кран. Для точек на краях поверхностный ток (А/м) мо жет (ыъ выражен через составляющие, нормальные и тангенгшаль 1[ые к гран1Ще:

мланарнои

(8 9)

где S п - единичные векторы, направленные тангенциально и нормаль но к границе, как показано на рис.8.2.Для точек на краях двумерного планарного компонента, где отсутствуют выводы нормальные состав ляющие поверхностного тока должны быть равны нулю:

dEJdn - О

(8 10)

Планарные компоненты могут возбуждаться двумя способами микрополосковыми (или полосковыми) линиями, соединенными с вы водами планарного компонента, или коаксиальными линиями. Если возбуждение осуществляется коаксиальной линией, как показано на рис. 8.4, ток течет от точки юзбуждения в направлении оси z. Через вывод, расположенный на краю планарного компонента, последний может возбуждаться с помощью полосковой (или микрополосковой) линии и в этом случае ток в сечении вывода направлен нормально к краю планарного компонента. Ток, протекающий в сечении вывода может быть получен из формулы (8.9):

jtufi

дЕ дп

(8 II)

где W - ширина вывода; ds - приращение расстояния вдоль края планарного компонента. Знак «минус» в формуле (8.11) означает, что ток i направлен внутрь компонента тогда как вектор п направлен наружу.

Характеристики планарных компонентов можно выразить через СВЧ напряжение v в центральном проводнике Для dEJdz - О из формулы (8.3) можно получить

и - - £, rf

(8.12) 143

Теперь уравнения (8 4), (8 10) и (8 И) можно записать в виде

(Vf+*)o-0 (8 13)

дг}1дп--0 (8.14)

для точек на краях планарного компонента за исключением точек выводов Ток выводов выражается формулой 2

ds

(8 15)

Решая (8.13) с граничными условиями (8.14) и (8 15), найдем характе ристини планарных компонентов полоскового типа. Уравнения для планарных цепей других типов могут быть получены аналогично Для описания планарных компонентов могут быть использованы раз личные приближенные методы Выбор того или иного метода опреде ляется геометрией центрального проводника планарного компонента Если планарная цепь имеет простую геометрическую форму, то наи более удобен приближенный метод, основанный на применении функ ций Грина, рассматриваемых в разд. 8.2 и 8.3. В настоящее нремя из вестны функции Грина для элементов прямоугольной или круглой фор мы в виде кольца, некоторых типов треугольника и в виде секторов круга и кольца. Использование функций Грина для перечисленных типов элементов позволяет получить их Z-матрицы

Если планарная цепь сложной геометрической формы может быть составлена из элементов более простои формы, для которых функции Грина известны, то для получения характеристик суммарной цепи, состоящей из этих элементов может использоваться метод сегментации. В некоторых случаях к элементу сложной формы можно добавить некоторый элемент простой формы (для которого функция Грина из вестна), чтобы полученная суммарная конфигурация также оказалась простой (для которой функция Грина также известна) Тогда для определения характеристик исходного элемента сложной формы на основании исследования простых по форме элементов может использоваться специальный метод, называемый методом десегментации. Методы сегментации и десегментации рассматриваются в разд, 8,4 и М.З.

Для анализа планарной цепи произвольной формы используются

численные методы. Один из них ......метод контурных интегралов - -

рассматривается в разд. 8.5

82 ПРИБЛИЖЕНИЯ С помощью ФУНКЦИЙ ГРИНА 3

Рассматриваемый мегод может использоваться в тех случаях, когда форма двумерных планарных компонентов сравнительно проста. Используя функции Грина, можно получить аналитическое выражение напряжения в произвольной точке прн возбуждении пленарного компонента единичным источником тока, расположенным в какой-либо заданной точке. С помощью функции Грина нетрудно получить Z-мат-рицу компонента с заданным распо.110жением его выводов

Рнс 8,5. Расположение в планарной цепи источников тока возбуждения /, (дгп, yt) и исследуемой точки (х, у)

Пусть планарныи компонент юзбуждается током плотностью У,, протекающим в направлении оси г через некоторую произвольную внутреннюю точку дго, (не лежащую на границе планарного компонента), как показано на рис, 8 5 Тогда волновое уравнение может быть записано в виде

(Vff ft*)!-- -]i\KdJ, (8 16)

Если планарная цепь возбуждается полосковой линией, то У, - плотность фиктивного СВЧ тока, текущего в направлении, нормальном плоскости компонента. Это значит, что ток линии плотностью J„ -2 dv

- -jjjjj теперь втекает в планарную цепь в местах расположения вводов на краях планарного компонента и можно считать, что запиты-вание осуществляется нормально (по оси z) с выполнением условий на личия магнитной стенки dvldn О иа протяжении всей границы планарного компонента. Это можно объяснить следующим образом. В центральном проводнике полосковой линии, соединенном с выводом планарного компонента, протекает ток, который втекает в этот компонент. В каждый нз заземленных пластин в обратном направлении текут токи равные половине этого входного тока. Можно считать, что на стыке центрального проводника полосковой линии и планарного компонента ток разветвляется на два эквивалентных тока, направленных вдоль оси г, как показано на рис. 8.6, Эти эквивалентные токи будут определены далее Напряженность магнигнсго поля на краях планарного компонента может быть рассчитана из (8 6) и (8.12):

]ci>[id \ дп ds J

Напряженность этого магнитного поля должна быть равна напряженности магнитного поля с противоположной стороны поверхности раздела между планарным компонентом и соединительной линией Если предположить наличие магнитной стенки вдоль всего края планарного компонента то тангенциальная составляющая напряженности магнитного поля на границе должна быть равна нулю. В настоящей модели имеется магнитное поле на краях (в местах расположения выводов) Эквивалентный фиктивный поверхностный ток f А/м в г-на