такие как согласованные нагрузки, изготовленные на линиях переда чи используемых в исследуемой схеме.

После того как найдены значения 5-параметров соединителей, их влияние на результаты измерений можно исключить с помощью мето ДА десегментации

103 МЕТОД ОБРАБОТКИ ДАННЫХ

Как уже отмечалось, калибровка неидеальных систем и определе ние характеристик соединителей осуществляются экспериментально с помощью многочисленных измерений с использованием стандартных нагрузок или проходных элементов. Для калибровки системы, пред назначенной для измерения двухполюсников, необходимы три отражательных образцовых компонента. Для измерения параметров четырех полюсников должны быть добавлены еще два образцовых компонента проходного типа. При измерениях параметров многонолнэсников требуется отдельно определять характеристики соединителей или переходников, для чего необходимы дополнительные измерения с двумя отрезками линий

Все последующие расчеты осуществляются решением системы ли нейных уравнений с числом неизвестных, равным числу независимых уравнений. При измерениях параметров двухполюсников решается система из трех линейных уравнений (10.12) при i 1. 2, 3 с тремя неизвестными /„„, г,, и При измерениях параметров четырехгюлюс-ников решаются две системы из двух уравнений каждая Из(!0 19) имеем

г,„Г,.(1 г,, г ,Т) i

(10 42)

Эта система уравнении содержит два неизвестных и гх,/,- Анало гичные уравнения относительно переменных /-„я и гах>1з можно полу чить в результате измерений при установке переключателя Кл1 в по лпжепие б При исследовании соединителей, описанном в разд 10-2.5. И1мсрение коэффициента передачи позволяет определить произведение i 5,;5.д, а два линейных уравнения, полученных из (10.37), определяют ! два неизвестных S и S.

В описанных случаях точность ишеренни можно увеличить уве личнвая число измерении по сравнению с минимально необходимым значением Результирующая система линейных уравнений может быть записана в виде

Лх. b (10 43)

где А- матрица размерностью ж/x п. m число измерений; п-число неизвестных, В рассматриваемом случае m > « Вектор х содержит п неизвестных которые должны быть найдены, а вектор b состоит из , ш измеренных значений. Вектор b содержащий т элементов, имеет возмущения возникающие из-за случайных погрешностей измерений что оказывает влияние на все т линейно независимых уравнений (

Так как матрица А является прямоугольной, то обычно этн уравне ПИЯ не имеют единственного решения. Они даже могут оказаться не совместными, В таких случаях х определяется из условия получения минимальной суммы квадратов [16!

Ax-b=-(Ax-b)*(Ax-b)- х*А* Ax-x*A*b b*Axb*b

(10 44)

Здесь индекс означает комплексно-сопряженное значение Диффе ренинрование (10.44) по х и приравнивание нулю дает

А* Ах Л*Ь ,10.45)

Теперь, если матрица А*А не вырожденная то имеется единственное решение

(10 46)

Этот метод обработки данных является весьма общим и использует ся в ЭВМ, управляющей измерителем для повышения точности измерений. Рассмотренные методы измерения и обработки данных могут ис-гюльзоваться для моделирования тех СВЧ компонентов аналитнче ские характеристики которых неизвестны

х-(А* А) А*Ь

Часть III АНАЛИЗ

Глава 11

РАСЧЕТ ХАРАКТЕРИСТИК ЦЕПЕЙ

Как отмечалось в гл 1 автоматическое проектирование состоит в многократном проведении анализа схем Анализ представляет собой расчет характеристик полной схемы на основе характеристик состав-1ЯЮЩНХ ее компонентов. В этой главе рассматриваются различные методы анализа СВЧ схем.

Как говорилось в предыдущих главах, СВЧ устройства наряду с компонентами с распределенными параметрами могут содержать компоненты с сосредоточенными параметрами. Элементы с сосредоточенными параметрами появляются либо в эквивалентных схемах моделей используемых активных приборов, либо непосредственно как элементы схемы Схемы с сосредоточенными параметрами обычно анализн-руютсяс помощью использования топологии ветвей-узлов [I] Полная схема описывается матрицей сопротивлений, проводимости или гиб ридной матрицей, К компонентам с распределенными параметрами относятся отрезки линий передачи, планарные элементы направленные ответвителн, циркуляторы и др. При анализе схем, содержащих компо неяты с распределенными параметрами, их представляют в внде многополюсников и полная схема обычно описывается параметрами рассеяния, Т- или ЛВСО-параметрами. Так как устройства в основном содержат компоненты и с сосредоточенными, и с распределенными пара метрами, то при анализе компоненты обоих типов описываются или эквивалентными схемами с сосредоточенными параметрами или много полюсниками. Как известно, компоненты с распределенными парамет рами могут быть представлены эквивалентной схемой с а>средоточеи ными параметрами только приближенно тогда как компоненты с сосредоточенными параметрами могут быть точноописаны как многопо тюсники [2]. Поэтому СВЧ устройства, как правило, в процессе ана лиза представляются многополюсниками. Как говорилось в гл, 2 четырехполюсные и многополнзсные схемы могут описываться S па раметрамн. тогда как четырехполюсные компоненты могут описываться также Д BCD и Г-матрицей.

П г СХЕМЫ СОСТОЯЩИЕ ИЗ ЧЕТЫРЕХПОЛЮСНИКОВ

Многие элементы используемые на СВЧ, являются четырехполкк никами, и, следовательно, большинство СВЧ устройств может быть представлено в виде комбинации только четырехполюсников. В этом

разделе рассматриваются методы анализа устройств состоящих нз че тырехполюсных компонентов. Четырехполюсники могут соединяться между собой каскадно, соединения могут быть последовательные, параллельные или гибридные. В результате последовательного или параллельного соединения четырехполюсников может быть получено многополюсное устройство

1111 ИСПОЛЬЗОВАНИЕ СИММЕТРИИ ПРИ АНАЛИЗЕ СХЕМ

Часто анализ многополюсных схем, обладающих симметрией относительно центральной плоскости, может осуществляться для двух схем, являющихся половинами исходной схемы, при четном и нечетном возбуждениях. При четном и нечетном возбуждениях можно рассматривать только половину схемы с одной стороны от плоскости симметрии, имеющую магнитную стенку в плоскости симметрии в случае четного возбуждения и электрическую - в случае нечетного

Половины симметричных четырехполюсников с четными и нечетны ми типами колебаний обычно являются двухполюсниками. Эти два двухполюсника анализируются с электрической и магнитной стенками а сечении плоскости симметрии. Схема симметричного четырехполюс ника показана на рис. 11.1а. Коэффициенты отражения рассчитываются для разомкнутой или короткозамкнутой схем в сечении плоскости симметрии, как показано на рис, 11.1 6. Матрица рассеяния первоначальной схемы четырехполюсника находится по формулам

Su = S,,-l/2{S„, + S„ ) 5„-5,,1/2(5h.--S„„)

(tl.la) (И 16)

Для симметричных восьмиполюсников (3 половины схем с четными и нечетными типами колебаний обычно являются четырехполюсниками Во многих случаях эти четырехполюсники в свою очередь могут быть представлены каскадным соединением четырехполюсников. Схема восьмиполюсника имеющая плоскость симметрии показана на рис, П-2а Она может исследоваться путем рассмотрения двух четырехполюсников, показанных на рис. 11,26 Матрица рассеяния полной схемы находится из матриц рассеяния половин схем с четным

Рис И.1 Схема четырехполюсника, имеющего плоскость симметрии (а) и его половины при четном и нечет ном типах колебаний (й)

I Магнитная Y стенка

•Электрическая стенка

[sl 5] о- [sjlo Sko] -

Pmc. И.2. Схема i

J прк четном н нечетном т

плоскость симметрии (а) и его колебаний (б)

н нечетным типами колебаний с помощью следующих соотноше НИИ 131:

5„S„ = i/2(S,.,+S2,„), (И 2)

S„S.,-l/2(S,j,-5„„). 5„=5з,..1/2 (S,„-S,,„). S,4-5„~=l/2(S,„-S,iJ,

Приведем несколько примеров восьми полюсных устройств, в которых могут быть использованы четные и нечетные типы колебаинк- Многосекиионный параллельно связанный направленный ответвигель (рис II 3) может анализироваться путем использования симметрии при четном и нечетном типах колебаний. Эти две схемы могут быгь представлены в виде каскадного соединения четырехполюсников. Другой пример шленфного направленного ответвителя показан на рнс, 11.4. Имеются н другие устройства, например фазовращатели, балансные смесители, анализ которых упрощается прн использовании плоскости симметрии. Итак, из зтнх примеров видно, что некоторые многополюсные устройства

могут исследовать

я методами <

1 четырех

1.3. TpexcehUHDHHUH параллель-Й направленный ответвигель (о), его половины при четном (б (в) типах колебаний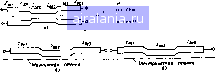

1112 КАСКАДНОЕ СОЕДИНЕНИЕ ЧЕТЫРЕХПОЛЮСНИКОВ

При исследовании схем состоящих из каскадно соединенных че тырехпа1юсииков, удобно использовать ABCD- или Т-матрииы 11ля полной схемы ЛбС£>- или Т-матрииа находится перемножением ABCD-или Г-матриц каскадируемых четырех пол нэсников Матрица ABCD схемы состоящей из N каскадно соединенных четырехполюсников показанных на рис 11.5 находится по формуле

(]] 3)

Индексы матриц в правой части выражения (11.3) означают номер со ответствуклцего этой матрице четырехполюсника. Матрица Т каскад ного соединения также находится перемножением 7"-матриц каскади руемых четырехполюсников

(П 4)

Итак анализ схем, состоящих из каскадно соединенных четырехпо 1ЮСНИКОВ, упрощается, если используются ABCD- или Г-матрицы так как в этих случаях для получения матрицы полной схйш необхо димо только перемножение матриц.

Как правило, СВЧ схемы описываются с помощью S матриц Сле довательно при каскадировании компонентов по их S-матрицам необходимо найти ABCD- или Г матрицы а затем по полученной ABCD- или Г-матрнце полной схемы найти ее S-матрицу Как говорилось в гл 2 Г-матрнцы имеют преимущества перед ylBCD-матрица-ми. Формулы для преобразования S-матриц в Г матрицы, S-матриц в /1ВС/>-матрнцы и обратно приведены в гл. 2.

Выразим матрицу рассеяния каскадного соединения четырехпо-лнзсников через матрицы рассеяния этих четырех пол нзснн ков. Пусть четырехполюсники А и В характеризуемые матрицами рассеяния S и S** соответственно, соединяются каскадно, как показано на рис 11 6 Если обозначить нормированные волновые переменные на

Рис 11,5. Каскадное соединение тырехполюсинкои

Рнс. 1L4. Направленный четном (б) н нечетном (в)

шлейфы

Рис 116 Каскадное соединение двух четырехполюсников Дай