входах двух четырехполюсников через а, Ьд а, записать

и т д то можно

(М,5а) (11 56) (П.6а) (11.66)

Если вход 2 четырехполюсника А и вход J четырехполюсника В име

ет одинаковые нормирующие сопротивления то

Ь,л -01л. (И 7а)

<1й-с2,1 П).7б)

Исключая hiA feiB ав и о. из \равнения (И .5) и (11 6) получаем

1 -Si, s.

i-sj,.s"

111 8)

Матрица в правой частн {11.8) является S матрицей каскадного соеди нения компонентов А и В. которую можно обозначить Зла »го соот ношение можно использовать неоднократно для получения S матрицы каскадного соединения большого числа четырехполюсников

1113 ПРОИЗВОЛЬНОЬ СОЕДИНЕНИЕ ЧЕТЫРЕХПОЛЮСНИКОВ

В результате некоторых соединении четырехполюсников может быть получена многополюсная схема. Некоторые примеры таких соедв нений показаны на риг 117 Для исследования таких схем можно вве-

гг-;т

5=: 1

Рис. 117 Примеры раз. 200

ырехполюсныл компо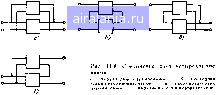

сти некоторые фиктивные многополюсники (на рис. 11 7 представле мы штриховыми линиями) определяющие необходимые соединения четырехполюсников. Затем можно использовать какой-либо из методов анализа соединений многополюсников, описанных в разд И 2 Для этого необходима S-матрица много полюсного соединения

В результате последовательного или параллельного соединения четырехполюсников [юлучается четырехгюлюсная схема (рис. 11.8) Для анализа этих схем могут использоваться Y-, Z /У-или С-матри цы 4. При параллельно-параллельном соединении четырехполюсников (рис. 11.8й) К-матрнца может быть получена простым сложением V-матриц двух компонентов. При последовательно-последовательном соединении (рис. 11.86) общая Z-матрнца получается сложением Z матриц компонентов. При последовательно-параллельном соединении четырехполюсников (рис, 11.8в) общая матрица схемы получается сложением Н-матриц а прн параллельно-последовательном соединении (рис. 11.8 г) - сложением G-матрнц компонентов. Кроме операций сложения матриц, необходимо еще выполнять однообразные, хотя и очень несложные действия, обеспечивающие получение К-, Z-. fi или G-натриц из S матриц, и нао(к)рот,

II 2 ПРОИЗВОЛЬНОЕ СОЕДИНЕНИЕ СХЕМ

В этом разделе рассматриваются методы определения параметров схем с произвольными внутренними соединениями

1 2 1 ИСПОЛЬЗОВАНИЕ ,МАТРИЦ РАССЕЯНИЯ СОЕДИНЕНИИ

Этот метод применяется в тех случаях, когда исследуемая схема шстонт из произвольно соединенных много1Юлюсников и независимых генераторов Будем считать, что схема содержит т многополюсных компонентов В этой схеме могут быть входы, не соединенные с другими входами, т, е- внешние входы Для /-го компонента с rii входами вхо дящие и выходящие волновые переменные (а и Ь- соответственно) on ределяются соотношением

/7f-S;a, (119)

Эт соотношение справедливо для всех компонентов за исключением независимых генераторов Независимые генераторы описываклея со отношением

6,--S,o, + c,

(11.10)

где - волновое описание генератора. Заметим, что в формуле (11 10) для развязанных (или согласованных) генераторов О

Для всех т компонентов в общем виде можно записать

Матрица S является диагональной, подматрицы ва диагонали которой есть матрицы рассеяния различных компонентов а О нулевые мат

""""уравнение (11.1) содержит характеристики отдельных компонен тов но не учитываетограничення. налагаемые внутренними соединениями Для каждой пары соединенных входов выходные волновые переменные одного входа должны быть равными входным волновым переменным другого если нормирование обоих соединяемых входов про изводите» аналогично. Если, например, вход, одного компонента соединяется с входом * другого как показано на рис. 11.9. то для входя " ших и выходящих волн должны вы

полниться соотношения

и 13) 1,13) яв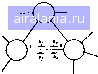

Рнс п.9, Соедннеине входа / од ного конпояента с входом к другого компонента

Матрица в правой части ляется обратной 5-матрице внутреннего соединения Элементы этой матрицы равны единицам или нулям, так как нормированные входные со противления для обоих входов оди маковы В том случае если нормиро-

вание входов / и ft неодинаково то элементы этой матрицы могут быть [юлучены путем нахождения обратной матрицы для соответствующей 5-матрицы соединения. Если нормированные входные сопротивления соединяемых входов состзвлякп- соответственно Zj и Zj, то эта матрица является обратной S матрице соединения двух линий с неравными волновыми сопротивлениями которая приведена в Приложении 2 1 (графа 9).

(ютношения (П.13) для всех внутренних соединений входов в схе ме могут &1ть записаны в форме

Ь-Га (11.14)

где Г - матрица соединений, описывающая топологию В каждой строке матрицы Г все элементы являются нулями кроме единицы, записанной в столбце, соответствующем внутренним соединениям. Если элемент (/, А) в матрице Г есть единица, то это означает, что вход / со едиияется с входом к. Как уже отмечалось элементы матрицы Г яв лнкпгся единицами или нулями только в том случае если нормнрукь щие сопротивления каждого соединения одинаковы.

Подставляя в (11.11) Ь из (11.14), получаем Га - Sa + с или (Г-5)а с (11 15)

(Г)бозначив

(И 16)

получим а - W с

(11 17)

В приведенных уравнениях вектор с описывает волновые переменные а матрица W называется матрицей рассеяния соединения. Элементы главной диагонали матрицы W являются коэффициентами отражений от соответствукдцих входов компонентов взятыми с обратным знаком; элементы матрицы, соответствующие различным входам компонента, представляют собой коэффициенты передачи с обратным знаком, а все остальные элементы матрицы являются нулями, за исключением элементов матрицы соответствующих двум соединяемым входам (элементы матрицы Г) Является ли элемент матрицы W нулевым или ненулевым, зависит только от топологии схемы и не зависит от значений параметров компонентов, их изменения или изменения частоты Значения ненулевых элементов матрицы при этом должны изменяться (за исключением единиц, которые определяются соеднкеннями). Решение (11.17) дает входные волны а на всех входах компонентов, а выходные волны Ь могут быть получены с помощью соотношения (11.14).

1122 МЕТОД МНОГОПОЛЮСНИКА [5J

Как н ранее, при этом методе матрица рассеяния схемы находятся на основе использования S-матрнц отдельных компонентов Этот метод применяется а тех случаях когда схема состоит из произвольно соединенных многополюсных компонентов и не содержит независимых генераторов Если имеется одни или несколько независимых генерато-

ров. то их можно выделить из ос новной схемы N (как показано на рис. 11.10) и определить для нее 5 матрицу.

Будем считать схему N многопо люсником (рис. 11,10) Эта схема содержит внутренних (соединяемых между собой) и р внешних входов. Если в схеме содержится т компонентов, то аналогично (1111) для всех компонентов можно записать

b Sa (11.18)

Строки и столбцы в (11,18) можно перегруппировать так чтобы волновые переменные разделились на две группы: первая соответство вала бы р внешним входам а вторая - с входам, соединенным внутри схемы. Тогда уравнение (11,18) можно записать в виде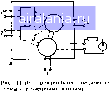

(И 19)

где Ьр, а,, - волновые переменные, соответствующие р внешним вхо дам; Ьг -- волновые переменные, соответствующие с внешним вхо дам. Ограничения накладываемые внутренними соединениями для с внутренних входов могут быть записаны в виде

(1120)

где Г - матрица соединений, получаемая тем же спосо(к)м, что и в подразд И 2.1. Из выражений (И 19) и (11 20) можно получить

Га, - S,pa„4 S,a,

a,-fГ-S„pS,,,a,,. (11 21)

Подставляя (П 21) в (.11-19) получаем

bp-lS,,-bSp,(r-S„)-S,pjap (И 22)

откуда матрица рассеяния

Sp-Spp-bSp,(r-S„) S,p. (И,23)

Уравнения (11-21) и (11.20) могут использоваться для получения волновых переменных на внутренних входах для любого произвольного способа возбуждения р внешних входов

Используя эту информацию и метод присоединенных схем, рассмат риваемый в гл 12 можно получить чувствительность параметров рассеяния схемы 204

Матрица (Г - в формулах (И 21) и (11.23) имеет свойства, ана логичные свойствам W-матрицы в формуле (11-16): матрица сильно разреженная а местоположение нулевых и ненулевых элементов оп ределяется только топологией и не зависит от параметров компонентов,

Несмотря на то что в этом подразделе предполагалось непосредственное соединение двух входов это не ограничивает род схем, которые могут исследоваться описанным выше методом. Любые другие соедине ння можно рассматривать в виде отдельных компонентов как описыва ,юсь в подразд, 11,1,3

1123 ПРИМЕР

Рассмотрим простую схему, показанную на рнс 11.11, и найдем для примера ее параметры способами, рассмотренными в подразд. 11 2.1 и 11.2.2. Схема состоит нз четырехполюсника А, описываемого матрицей S- шестиполюсника В, описываемого матрицей S, и двухполнхника С, описываемого матрицей S. В этом случае может непосредственно использоваться метод, описанный в подразд П,2.2 Нумерация вхо дов показана на рисунке. Запишем параметры всех трех компонентов в виде (11-19)

Матрица соединении Г может быть записана в виде

(11 24)

(11 25)

Рис 11 И Пример с