Полную матрицу рассеяния найдем мо форму1е (И 23) используя 111,24) и (11,25):

О Sf,

О О О О О ,S», Sf

- Si, 0 0 1

О - S 1 О

0 1 Sf, -SJ

1 О - Sf - Sf

s; 0

0 0

0 S"

L 0 Sf, J

(11 26)

При произвольных входных сигналах иа внешних входах входные вол новые переменные внутренних входов mocvt быть найдены по формуле (1121)

S?, О О 1

о S<: \ О

0 1 S» -Sf

1 O-Sf, -Sf

(II 271

Выходные волновые неременные \Ь.ф„Ьфя\ внутренних входов могут быть найдены подстановкой полученных выражений в формулу (И 25)

Чтобы найти S-параметры рассматриваемой схемы методом они санным в подразд. П.2.1, подключим независимые генераторы к внешним входам. Генераторы (на рис. П.П показаны штриховой линией) являются единственными компонентами входов и описываются формулами

h, = c, h,=c

(11 28)

Соотношения между banc для всех комтюнентов схемы могут быть теперь записаны в форме выражения (П.П)

(11 29)

Матрица внутренних соединений Г теперь принимает вид

(И 30,

входов

(11 31)

Выходные волновые неременные для всех входов Ь определяются по формулам (11.30) и (II.3I).

Эгнм способом могут быть найдены значения волновых переменных на всех входах для любых комбинаций значений Ci и е.. Если с, 1, а = О, значения hi и ft* (на внешних входах) соответствуют значениям "Sn и Sj, полной матрицы рассеяния. Аналогично для Ci О и Са -- 1 параметры Sj и соответствуют значениям hi и fej.

И 2 4 ЧРТОД ПОДСХЕМ [6]

Используя метод описанный в подразд И.2.2, можно получить S-матрнцу схемы с многополюсными компонентами, Согласно этому требуется находить обратную матрицу для матрицы, порядок которой равен числу внутренних соединенных входов. Если схема содержит большое число внутренних соединений, то порядок матрицы, для кото рой Ищется обратная матрица, становится очень (к)льшим. Вычислительные затраты при определении обратной матрицы могут лыть сниже ны, если рассчитывать не полную схему, а расчленить ее на несколько подсхем. Раздельно получают S-матрицы подсхем, а затем, объединяя их, S-матрнцу полной схемы, гот метод исследован в [6] и использо ван прн разработке программы анализа СВЧ схем (6,

Определение вычислительных затрат. Для схем, содержащих р внешних входов и с входов, соединенных внутри схемы, число дли тельных операций, требуемых для нахождения 5,,-матрнцы в выраже НИИ (11.23) определяется по формуле

N рс грс-аг* (И 32)

где первые два члена появляются из-за перемножения матриц а тре тий - из-за вычисления обратной матрицы размером схе. Коэффи циент а является константой и определяется алгоритмом вычисления обратной матрицы Значение этого коэффициента близко к единице Длительными операциями считаются операции умножения или деле ния двух чисел, так как время, требуемое для выполнения этих опера ций, намного больше времени, затрачиваемого на сложение или вычитание Как видно нз формулы (11.32). необходимое время вычислений быстро возрастает с ростом с.

Представим схему в виде двух подсхем R а R соединенных, как 1Юказано на рис. 11.12, Полная матрица рассеяния может быть определена в три этапа. На первых двух этапах раздельно определяются S матрицы двух подсхем а на третьем - обе подсхемы объединяются вместе. В этом случае суммарное число длительных операций, требуемое для вычисления S-матрицы может быть найдено по формуле (11.32) для каждого этапа

N,--p]Ci-rpiC\-\-ac\ + pU2 + Pzi2 t-ac + pc* f + pc*+ac*

(11 33)

Где Pi, рг. fj, - число внешних и внутренних входов для каждой из подсхем R и R" соответственно; с* - число соединенных входов между обеими подсхемами. Если предположить что обе подсхемы нме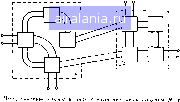

ют одинаковое число внешних входов и одинаковое число внутренних входов, то

Р.-р-г-Лр с*)/2. с,- г-(с-с%2.

(И 34а) (11 346)

Напомним что г с -\- -1-е* Подставляя /?, р г, в фор м\лу (11 33) пол\чаем

.V, "y -гас) + (л -рс + асП

- -~{3<X~\)(i-L*)Lt* (11 35)

Число длительных операции, определяемое формулой (11,35), меньше числа длительных операций, определяемых по (11,32), Распространяя описанное разделение иа каждую подсхему, получаем, что более быстрым расчет S-матрицы полной схемы получается при сложении на каждом шаге только двух компонентов Если схема содержит т компонентов, то формула (N23) используется {т - I) раз.

Желательно определить оптимальный порядок, при котором компо центы объединяются таким образом, чтобы суммарное число длительных операций было минимальным. Алгоритм, [юзволяющий определить порядок, близкий к оптимальному, предложен в работе [б! В ней сформулировано следующее правило, на каждом этапе должна объединяться та пара компонентов в результате объединения которой получается минимальное число внепжих входов Пример использова ния этого правила показан на рис. 11.13 Первыми в подсхему ВС объ единяются компоненты В и С. Затем объединяются компоненты Г и £ а потом компоненты Л и ВС После этого объединяются компоненты f£ и D и. наконец компоненты Л ВС и FfD В результате может быть

найдена 5-матрнца полной схемы исследуемого четырехпадюсиика. Последовательные изменения топологии на каждом шаге показаны на рис. П 136

Так как при объединении двух многополюсных компонентов для получения 5„-матрицы уравнение (11,23) используется неоднократно то же.1ательно улучшить метод решения этого уравнения. В данном случае, когда объединяются только два компонента, улучшение возможно. Нсли соединяются с входов, то их разделяют на две группы 9 и г так, чтобы группа q содержала входы одного компонента а группа г другого. Затем входы в обоих подгруппах нумеруют так чтобы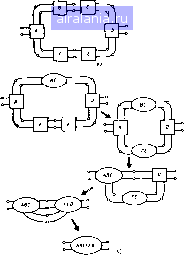

Рнс. 11.13, Прнмер расчета схемы методом подсхем {а) к последовательное i 1 при использовании этого метода (б)

вход 9, соединялся с входом г,, вход! с входом Гг и 1 д Теперь мат рина компонентов может быть записана в виде

s„, s„ s,

S„ S„ 0 S,„ 0 s„

(11 36)

в jtom уравнении нулевые матрицы S и S, обозначены О ц- иге входы принадлежат различным компонентам) Латрица соединении л-зя этого случая имеет вид

(П 37)

-Матрица (Г - S,.), для которой сопасно (11 23) определяется обрат ная матрица, имеет вид

-S„ I 1 -S

Теперь дтя матрицы (Г

(11 38)

S ) можно найти обратную матрицу

fll 39)

Здесь требуется вычисление двух обратных матриц порядка с/2. Возможны и дальнейшие упрощения путем разделения р внешних входов * группы: входы рх компонента / и входы компонента 2 Под-I S п имеют вид

атрицы S,„,

дс индексы 1 и 2 означают грушты р, и р соответственно Теперь может быть найдена полная S матрица схемы

s,„ • S„,M„S„,

(11 40) (II 411 (11 42)

(11 43,

В этом случае требуется меньшее число длительных операции, чем в е.1учае непосредственного использования формулы (11.23), так как !десь определяклея две обратные матрицы порядка с/2 и умножаются матрицы также меньшего порядка