скольку при анализе схемы требуется нахождение обратной матрицы при определении чувствительности больших схем такой вычислитель ный процесс неэффективен. Другим недостатком этого метода при малых значениях Ад: является необходимость вычисления в соответствии с формулой (12.5) разности двух близких значений, что может привести к большим погрешностям. Для больших значений Ах* точ ность исходной формулы (12.5) ухудшается. Из-за этих недостатков бо нее предпочтительным является метод присоединенных схем.

12 2 МЕТОД ПРИСОЕДИНЕННЫХ СХЕМ (5)

Метод присоединенных схем предполагает проведение анализа не чодной схемы и вспомогательной, так называемой присоединенной схе мы, которая образуется нз исходной схемы. Анализ этих двух схем позволяет определить чувствительность относительно всех переменных схемы Перед рассмотрением метода присоединенных схем, позволяю щего получить чувствительность параметров рассеяния, остановим ся на основной теореме. Такой теоремой можно считать теорему Тел легена для волновых переменных

12 2 1 ТЕОРЕМА ТЕЛЛЕГЕНА ДЛЯ ВОЛНОВЫХ ПЕРЕМЕННЫХ

Будем считать что основная схема состоит из многополюсных ком понентов. Пусть а и Ь являются нормированными входными и вы ходнымн волновыми переменными всех выводов рассматриваемой схе мы. Будем считать, что вспомогательная схема, также состоящая из многополюсных компонентов имеет нормированные входные и выход ные волновые переменные на всех входах аир. Разобьем эти две схе мы на подсхемы так, чтобы выполнялись следующие условия; I) тоно логин двух подсхем должны быть идентичными; 2) все выводы должны содержаться внутри подсхемы; 3) нормирование на соответствующих выводах двух [юдсхем производится аналогичным образом. Второе ус ловие означает, что внешние выводы из подсхем исключаются Пример двух подсхем, удовлетворяющих этим условиям, показан на рнс. 12,1 Если я, и являются входными и выходными волновыми перемен ными всех выводов внутри подсхем то они связаны соотношением

b Г, а (12.6)

где Г,- матрица внутренних соединений, определяемая топологией и нормировкой подсхемы Метод получения матрицы внутренних соединений рассматривался в подразд. 11.2.1. Согласно принятым здесь условиям соответствующие входные и выходные волновые переменные а, и р во вспомогательной подсхеме связаны тон же матрицей внутренних соединений Г,:

(12 7*

Используя (12 6) и (12 7) можно показать что для случая Г, - Г Ыа - а; р, а,(Г, Г,,а, -О (12.8,

12,1, Пример з.яух подсхем (летворяющнх теореме Теллегеиа

Этот результат имеет силу для любых двухподсхем с одинаковой то гюлогией. Следовательно, он также имеет силу для двух полных схем с одинаковой топологией. Внешние входы полных схем соединяются либо с генераторами либо с на грузками.

Уравнение (12.8) может быть обобщено для случая двух схем одинаковой топологии с внешними входами Внутренние входы в обеих схемах удовлетворяют урав нению (12.8)

Ь;,а ар,=0

Отсюда можно записать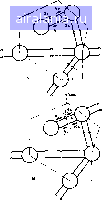

(52 9)

где индексом «р», как и в гл 11 обозначены волновые переменные внешних входов, а индексом «с» - вотовые переменные соединенных внутренних входов

12 2 2 ПРИСОЕДИНЕННАЯ СХЕМА

Будем считать, что основная схема состоит из много полюсных ком понентов. Пусть параметр схемы ф имеет небольшое отклонение. В СВ ч схемах этим параметром может быть волновое сопротивление, длина линии и др. Рассмотрим влияние изменения параметра (р на характеристики много полюсного компонента. Если этот компонент характеризуется матрицей рассеяния S так что b = Sa

,5ф *р

(12 II)

В выражении (12.9) члены, содержащие а и Ь, могут быть заменены со ответствующнми частными производными по ф:

дь да \K*f Ч"1- Р Ч"! (12 12)

ч Зэк 2259

де переменные аир относятся к вспомогательной схеме описанной в подразд. 12.2.1. В правой части уравнения (12.12) член, связанный с рассматриваемым компонентом может быть записан в виде

adb"d<f-fd i/dif (12 13)

Используя формулу (12 11) последнее выражение можно преобразо вать к виду к

US , а а

-(S а-р

(12 14)

в этом выражении а и р - входные и выходные волновые переменные соответствующие входам компонента, на которые оказывает влияние параметр ф во вспомогательной схеме, имеющей идентичную топологию с исходной схемой. Если дтя рассматриваемого ком1юне[!та опреде-

(12 15)

Р- S а

то выражение (12 14) преобразуется к вид; , dS

-" (12 16)

Если все компоненты вспомогательной схемы определены аналогично (12 1.5). то эта схема, описываемая переменными аир. называется при соединенной для исходной схемы.

Правая часть уравнения (12.12) может быть преобразована с по мощью выражения, аналогичного (12.14) для каждого компонента схе мы Тогда уравнение (12 12) примет вид а Ь1 дл

Так как все компоненты присоединенной схемы определяются уравне нием

Sa ,12 18)

то (12.17) преобразуется к уравнению

(1219)

Обычно изменение параметра ф влияет на характеристики только одно го компонента, а характеристики других компонентов остаются неизменными Для этого случая

где a, S и a соответствуют компоненту зависящему от ф; значение dSldif для других компонентов берется равным нулю. Можно показать, что если изменение параметра ф влияет иа характеристики более чем одного компонента, то в правой части уравнения (12.20) должны быть [1росуммированы члены, соответствующие всем таким компонентам. Например, если определяется чувствительность ГВЗ относительно час готы то в правой части уравнения (12.20) должны быть просуммированы члены, соответствующие всем частотно-зависимым компонентам схемы.

Если схема согласована по всем внешним входам то производные dSfldff =г- о. Тогда уравнение (12.20) преобразуется к виду

Л5! (

2«»

(12 21а)

(12.216)

где £ - множество р внешних входов. Легко видеть, что уравнения (12.21) устанавливают связь между изменениями выходных сигналов на BHeuniHX входах и изменениями характеристик компонента, завися-Ш.ИХ от изменения ф и, таким образом, определяют чувствительность выходных сигналов относительно ф. Чувствительность относительно других параметров может быть найдена дифференцированием правой части (12.21). Это требует нахождения частных производных подматриц компонентов. Они рассматриваются в следующем подразделе. Чув-ствнте.1ьность относительно всех параметров может быть найдена проведением анализа двух схем - исходной и присоединенной. Если компонент удовлетворяет условию взаимности, то S - S и присоединенная схема содержит исходный компонент. Если все компоненты являются взаимными, то присоединенная схема совпадает с исходной.

Вычисление градиентов. Будем считать, что известна матрица рас сеяния схемы, для которой определяется градиент коэффициента S,j. Пела i ф 1 вносимые потерн от входа f к входу / определяются форму юй.

(12 22)

при условии что все другие члены (к =?= f) равны нулю (другими (.•ловами, при условии, что /-Й внешний вход возбуждается согласо-панным генератором, а все другие внещние входы нагружены на согла-

ованные нагрузки). Если й, I формулу (12.216) можно представить

i виде

(12 23)

Теперь если итожить а к£ Е то получим

1 а все остальные значения i

(12 24)

где (-Й внешний вход в присоединенной схеме возбуждается гогла сованным генератором а все оста1ьные нагружены согласованными на грузками

Градиенты любою коэффициента S,j определяются соответствую [цим возбуждением исходной и нригоедииепной схем (как уже говори лось, а, - <х{ 1), Ксли требуется определить градиент коэффициента отражения от внешнего входа схемы, все компоненты которой удов летворяют условию взаимности, то [1рисоединенная схема совпадает с исходной и возбуждается тем же способом. Следовательно, в этом слу чае для вычисления градиента требуется выполнить анализ только один раз.

Анализ присоединенной схемы не требует больших дополншельных затрат. При испо.!1Ь.зованни рассмотренного в подразд, 11.2.1 метода матриц рассеяния соединений матрипа в выражении (11.17) пре образуется из матрицы W" исходной схемы, а для взаимных схем сов падает с матрицей W" исходной схемы. Матрица присоединенной схемы легко определяется и для получения волновых переменных внут ри схемы она умножается на вектор с. Если присоединенная схема ана лнзируется рассмотренным в подразд. 11.2.2 методом многополюсника то (Г - Sfc.)" г,, Д-я присоединенной схемы легко определить из анализа исходной схемы и, используя (11.25), найти волновые пере меиные внутри схемы для любого возбуждения а,.

Уже говорилось, что определение чувствительностей для присоедн пенных схем может быть использовано для получения производных второго порядка матрицы рассеяния схемы по различным параметрам Для этой цели требуются производные входных волновых переменных на входах относительно параметров схемы. Анализ присоединенной схемы должен быть выполнен несколько раз, Более подробно получе ние производных второго порядка описано в (51.

1223 СРАННЬНИе с ПРЯМЫМ МЕТОДОМ

Рассмотрим каскадное соединение двух четырехполюсников, пока занное на рис. 11,6, Полная S-матрица каскадного соединения записа на в (11,8). Будем считать, что возмущение параметра л: 1Юлностью со держится в ком1Юненте Л т е изменение параметра jc не влияет на ха рактеристики компонента В Используя (11,8), можно непосредствен но записать производную S! относительно переменной х

s, (sb )2 5

(12 25)

I ли компонент A является взаимным то S, - S. и формула (12 25) южет быть преобразована

(12 26)

!е же результаты 1юлучены далее методом присоединенных схем. Ест fi6a компонента являются взаимными, то присоединенная схема совпа чает с исходной. Для получения производной 5,, обе схемы возбужда ются единичным источником на входе / исходной схемы. Входные вол гювые переменные двух входов компонента А могут быть найдены с по мощью (11 21):

!кл sb 1

(12 27)

Г.огласно (12 24) производная Sl может быть записана в виде форму

(12 28)

которая 1юсле умножения совпадает с (12.26).

Если для компонента В условие взаимности не выполняется, то }юрмула (12.27) остается справедливой и метод присоединенных схем лает тот же резу.пьтат, что и (12.26).

2 24 Р\СЧЕТ ГРАДИЕНТОВ ДЛЯ МРТОДА ПОДСХЕМ 4 6]

Для нахождения чувствительностей методом присоединенных схем должны быть известны значения волновых переменных на всех входах компонентов, зависящих от исследуемого параметра. При анализе схем мето.аом подсхем (см. в подразд, 11.2.4) в каждый момент времени рас 1магрнвается только один компонент и волновые переменные на всех иходах компонентов остаются неизвестными В данном подразделе рассматривается способ, позволяющий получить волновые переменные на f!cex входах компонентов, при подобном анализе 161. В этом случае процедура анализа несколько изменяется: каждый компонент добав

шется к уже сформированной подсхеме. Производится наращивание I хемы путем подключения каждого многополюсного компонента к . [к)рмированной ранее подсхеме. Если к одной и той же подсхеме тре оуется подключить более одного компонента, то для определения того какой из компонентов должен подключаться первым, необходимо ноль

юваться следующим правилом. Первым должен подключаться тот мно инголюсник, в результате подключения которого в полученной под \еме образуется наименьшее число полюсов.

Пусть схема состоит из т многополюсных компонентов. В соответ-пши с изложенным в процессе анализа для формирования подсхемы