компоненты подключаются один за другим. Обозначим через Е, k и т порядку компонент, а через 2 - подсхему сформированную пос ле соединения it компонентов. Подсхему 2 можно представить в виде внутреннего соединения подсхемы , с компонентом Е. Волно вые переменные а (Е, на входах, соединяющих элементы

и £й, могут быгь выражены через волновые переменные (2) на входах подсхемы 2,,. В момент соединения двух подсхем для анализа используется процедура, описываемая формулами (11.36) - (11.44) Выделим подгруппу волновых переменных а (£j, 2 ,) из волновых переменных а„ (Е,,) и (2,) на входах элементов £ и соот ветственно Аналогично выделим подгруппу а,, (2,,) из волновых переменных Эр (£й 2„) и ар [2,, ,. 2) на входах элементов £], и 2 з соответственно Тогда можно записать

а,(> • «)

(12 29)

где Ph - квадратная матрица, состоящая из единиц и нуле( которая необходима для перегруппировки переменных в Яр (2).

Согласно (11.44) можно выразить (£,, h-i) через Вр (2)

аИЕ. I. ,) [;;!» R.f"-" X.->.»,.(..).

[ас(2* i)j [ар(2* 2)]

(12 30)

где Rfc выражается через 1юдматрицы (П.44)

Целью здесь является выражение волновых переменных внутри схемы iV через волновые переменные на внешних входах. Чтобы этого достигнуть, воспользуемся выражением (12.30) для получения вол новых переменных между £„ и 2„ ,, затем используем их для полу чения волновых переменных между Ещ , и 2„ и т, д. Волновые переменные на входах, соединякмцих элементы £,,„ и 2„ j найдем на ос новании (12.30) (при k = т)

a,(fm S„) И-

Внешние входы i-™ , состоят из внещних входов 2 одновременно являющихся входами m~i и входов, соединяющих элементы 2„, j и £„ входящих в состав входов S,. Это показано на рис. 12 2, Так, Лр (2„ j) состоит из Яр (2„ i, 2„) и а (2„ ):

г, (2-1 2)

Л„ Р„а„(5:„)

(1231)

а„(2:„ ,)-

а, (2„ ,)

(12 32)

Получить Эр (£m i Sm) МОЖНО ИЗ Зр (2 „) вычеркиваиисм строк, соответствующих волнам, не поступающим на 2.-1- Аналогично переменные а. (2,п ,) могут быть получены из правой части (12.31) вычеркиванием строк (RmPm). соответствующих волнам не постугающим на 2„ 1 Обозначим операцию вычеркивания строк знаком [„,..,. 230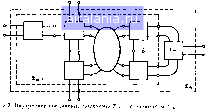

Тогда из (12 31) и (12..Э2) имеем 1(1)

а, (i.., ,) -

(RmPm) I.

(12 33а)

r,ie I (п) - единичная матри[1а. имеющая размер п равный числу внешних входов схемы. Уравнение (12.33а) .может быть переписано в виде

а, (2» .) Т„ ,а,(2:„)

l(")U . (R„P„,r„-,

(12 336)

(12 34)

Чтобы продолжить обратную подстановку необходимо [leperpyn пировать переменные в а (S„ ,) в подгруппы а., (f „, , 2„ ,) и а, (-m-s. mi] Продолжая так же как и ранее

а,(£„ . 2„->)"-.Rm ,Р.. .Т„ ,a,(Sj что дает

""->"[(r1-!,P„-,T„ „„ , Следовательно для произвольного k а„(2.)- Т,а(2.)

получаем

(12 35)

аИ2».) Т„ ,a,.(S„) (12 36) (12 37а)

(R»+, Р»„Т,„).

(R.»P».)i.

(R„-,P„ ,Т„

(R„,P..,n+,)l.

(12 376)

(12 38)

в конце процесса обратной подстановки (т. е. когда k = 1) все падаю щне волны на всех компонентах можно записать совместно

а ,£„ 2„ i) RP„

Пример. Г1римени с. 11 Мо Эта схема повторена на pv чена последовательность подключен нентоБ m -- 6. а число внешних bxi

nocie соединения имеем

{<,а Re Р« 1". «и1

а, (2,

(12 39)

R J Pi Т.

Итак с помощью некоторых дополнительных вычислений волновые пе ременные на всех внутренних входах выражены через волновые пере менные на внешних входах схемы.

фоцед\ру к схеме приведенной на \1 3 на котором буквами .Е* обоз-

ик.)-

Продолжая itex внутренни

123 ПРОИЗВОДНЫЕ МАТРИЦ РАССЕЯНИЯ

(12 456) переменные

В этом разделе будут получены частные производные S-матриц (й5/ф)для некоторых типовых элементов. Цля получения этих про изводных используются инварианты чувствительности 5-матрнц, яв 1якнциеся предметом рассмотрения следующего подраздела.

где Ре - единичная матрица. Re - матриил ра,!.иеро подматриц в соответствии с (II 44) Иа (12 40) можно п< черкивання двух последних строк из / Рв. что со Таким обра.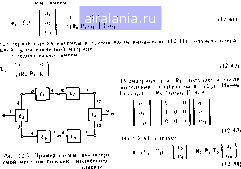

иаиным зля вычисления гр: 232

12,3 1. ИЫВ\РИДНТЫ ЧУВСТВИТЕЛЬНОСТИ S МАТРИЦ [7]

Существунэт некоторые инварианты чувствительности для схем со стоящих из сосредоточенных резисторов, катушек индуктивности конденсаторов, однородных линий передачи и управляемых источнн ков. Эти инварианты чувствительности для S матриц получены путем первоначального рассмотрения инвариантов чувствительности для Z матриц. С учетом присоединенной схемы Л теорему Теллегена можно (аписать в виде

(12 46)

где v v,. соответственно напряжения на внутренних и внешних вхо дах исходной схемы; i, - токн в-соответствующих входах присоеди ценной схемы. Нормированная чувствительность элемента ((. /) пол ной матрицы сопротивлений относительно параметра содержится в элементе матрицы сопротивлений Zp

(12 47)

де is 1д токи входов компонента д1Я присоединенной и исходной схем соответственно. Здесь предполагается, что исходная схема воз буждается единичным током источника на входе /, присоединенная схе ма возбуждается единичным током источника на входе i, а все осталь ные входы обеих схем разомкнуты.

Переменные отдельных компонентов обозначаются следующим об разом; Li, £>; 1/С; - соответственно для резисторов, катушек индуктивности конденсаторов с сосредоточенными параметрами; Z; - vin волновых сопротивлений однородных линий передачи и - для

сопротивлении передачи источников напряжении управляемых током Итак, положим

{г} [R, L D Z,r„,} (12 48)

Если является одним из параметров, перечисленных в (12.48). то компонент, который его содержит, описывается однородной матрицей сопротивлений первой степени Другими словами если содержится в то

рАФй - (12 49а)

а если не содержится в Z то

р,- о (12 496)

Из (12 49а) и (12.47) следует что если содержитея в Z то

(12 50)

Суммируя по всем параметрам записанным в (12 48) потучаем

(1251)

ли с учетом (12 46) записываем

(1252)

Так как присоединенная схема возбуждается единичным током источни ка с внешнего входа с, а все остальные внешние входы разомкнуты, то правая часть уравнения (12.52) равна и,. С другой стороны, поскольку исходная схема возбуждается током источника в виде единичной сту пенчатой функции с внешнего входа /. а все остальные входы ра зомкнуты то

Vj z„i, г,

Из (12-52) и (12 53) следует что

Так как обозначения (i /) были выбраны произвольно то

X "

Из (12.54) следует

(12 53) (12 54)

(12=>5)

(12 56)

Сумма нормированных чувствнтельностей равна единице независимо t>t значений Z,j. Как уже говорилось, если матрицы сопротивлений компонентов являются однородными первой степени относительно па раметров сопротивлений (12.48), то согласно (12.49) полная Z-матри ца характеризуется теми же свойствами

Чтобы получить инварианты чувствительности дчя S-матрицы схе мы, вылазим S через Z сопасно (2 36) и поспе дифференцирования за

2\l-z

t 4) u z„

(12 57)

Производя суммирование p (dS ф) гю всем p, определенным cor lacHo (12.48) (за исключением нормирующих сопротивлений Za, всех зходов), имеем

Z.)- 4KZ.i (12 58)

НЛИ с учетом (12.55)

(Z -Z) iZ(Z Z,)

j(Z„j.--i-<I s,

(12 59)

1де произведение S на себя и единичную матрицу I.

Заметим, что в (12,58) не производится суммирования но нормирую uiHM сопротивлениям. Если суммирование производится по всем нор мирующим сопротивлениям то

2» -21 z;(Z + Z,) Чz;l2KZ",j(Z

+ Z,) z.(Zi z,, irz;i ~2\\ z„\(z +

bZ,) •z(z + z,) Irzll -j-(S-l) (12 60)

Из (12.59) и (12.60) следует, что если [1роизводить суммирование по всем параметрам в {г} так же, как по всем Z„,, то получим

(1261)

где pk параметры в {Z), включая и нормирующие сопротивления Можно показать, что р могут являться также соответствующими пара метрами Проводимости, и в этих случаях правая часть выражения (12.59) отрицательна. Отсюда сумма чувствнтельностей относительно тех {г} или {у} параметров схемы, включая нормирующие сопротив ления или проводимости для любых схем равна нулю.

Используется общая формула