сии суммы случайных переменных (Приложение 13 1) можно чанисать дисперсию и в виде

др..

(13 20)

где R - матрица корреляции параметра р/. Таким образом, можно определить дисперсию эксплуатационного параметра, если известны дисперсии конструктивных параметров р, и чувствительности Эту процедуру проиллюстрируем иа [!римере.

Пример. Рассмотрим рассогласование между сопротивлениям! релеляемое коэффициентом отражения р Даны десять пар аыборои сопротивлений и Z. Их корреляция вычисляется с помощью Д веденных в табл. 1.3 1

1ИЙ расчет выполним следующим образом 1ения Z, 52.0 и Z, - 49.5. (дратические отклонения

Zi и Zi. t

!ИИЙ

Средние з

- ПО 3 42

Средине

Коэффициент Koppeii -90,00

тедовагельно среднее значение коэффициеи! Р (Z- Z,) {Z, 1 Z) -0,024Ь Из определения коэффициента отражения

rfZ,

Л еперь м

(Z, Z,И 2Z,

-О 00%! О 0101

дисперсии коэффнш -if

c)Z, dZ,

I- О 0319 О Щ/П а„ 0.0643

1 0.7.(81

О 73« 1 L

0.03191

Полученное значение дисперсии ми) жеиия р для каждой лары сопротив

13 22 ЧРТОД ЧОНТЕ КАРЛО

Этот метод может быть использован тогда когда неизвестны значе иня чувствител ьностей или рассматриванзтся большие статистические колебания

В этом методе генерируются множеством значений параметров, ко горые определяются их статистическими распределениями. Затем анализируется схема и определяются эксплуатационные параметры, соответствующие значениям этих множеств параметров. (!;татистические данные об этих эксг[луатационных параметрах дают информацию об нх возможных отклонениях.

Процедура имитирует множества значений параметров соответст вующих заданному распределению. Для этой цели требуется генерация случайных чисел, соответствующих заданному распределению В большинстве ЭВМ имеются стандартные подпрограммы для генерации случайных чисел, равномерно распределенных на интервале [0,1]. Исполь-!уя эти равномерно распределенные случайные числа можно получить случайные числа для искомого распределения. Для этого требуется ин гегрнрование функции плотности вероятности. Значения параметров .1ля заданного распределения в заданной области изменений могут быть 1юлучены пересчетом случайных чисел распределенных на интервале 10 II

Полученные таким способом значении параметров случайным обра-юм объединяются с другими параметрами (образованными аналогичным способом) и формируются в группы Каждая группа значений па раметров описывает анализируемую схему. Анализируя большое число таких имитируемых схем, нетрудно [юлучить статистические распределения эксплуатационных параметров

Средние квадрзтнческие отклонения рассчитанные на основе статистических распределений, дают более реальные значения максимальных отклонений от номинальных значений. Из этих распределений может быть также определен процент выхода годных (процент уст ройств, удовлетворяющих заданным требованиям).

Рассмотренные в зтой главе методы анализа наихудшего случая и статистического анализа отклонений характеристик от номинальных значений могут использоваться для расчета и выбора допустимых от клонений

ПРИЛОЖЕНИИ 13 i

НЕКОТОРЫе ПОЛОЖЕНИЯ ТЕОРИИ ВЕРОЯТНОСТЕЯ и СТАТИСТИКИ (2, 8]

В этом ггриложекии дается краткий обзор иекоторых результатов теории вероятностей и статистики для непрерывно изменяющихся параметров.

Рассмотрим случайную переменную х. которая непрерывно изменяется от нижней границы i, до верхней границы xj. Функция плотности вероятностей А (.г) в области (ж,. хг) определяется так. что значение Л (i) dr означает вероят ность появления случайной переменной а области (jt. х ilx). Функ должна быть не отрицательна в области {х-, xj, а ее интеграл в пределах дает вероятность появления случайной величины в этом интервале

я h {х\

\ k{x) dx =Р (о < j

где xiu<b< xj. Среднее значен» определяютсд формулами

] лЛ {x) dx

о2 J (л -x) h (х) dx

Если переменная х равномерно распр» функции А (д:) определяется формулой

Другим примером непрерывного распределени распределение, определяемое формулой

(ШЗ 1)

Й величины x и ее дис 1ерсия ffl)3 2) (ПП 3)

)трезке {х, ч,( распреде1ение (П13 4)

Дискретный случай. В некоторых случаях случайная переменная принимать дискретные значения xi. х, . . хп. Среднее значение и днсперся: случае определяются формулами

, V

(1113 ()

(Пи 7)

умножить hd коэффициент А то дисперсия а- возраст* : раз, а среднее значение - а Л раз.

Независимые переменные. Две случайные переменные х м у йвиснмыми тогда и только тогда, когда распределение переменной i в о le зависит от распределения переменной у. Математически это выра) ледующии бра юм

я любых возможных интервалов (о, ь) и (с. d)

Коррелированные переменные. Коэффициеиг е слуайные переменные jc н v для дискретного сп

< d

моррелипин. связывающий (эн. определяется формулой

f -~ лиспер!

2 П (.1/, -и}-

учайныл вели

НПЗ 9,

elли переменные

1ы. их коэффициенг корреляции равен ну.ш и эти переменные не коррелированы Однако обратное неверно, т е если г - О (переменные некор релировапы), то это не означает, что эти переменные независимы Коэффициент корреляции случайной переменной по отношению к самой себе равен I

Для случайных переменных х,. х. . . х„ можно определить матрицу корре 1нции R размера п п. так что г,, rj, задает коэффициент корреляции между г еременными х, н к,

Лнсперсни случайн н перемеинги х задан и как

у <• (III:! ini

он ) еде.! я етс н фо р ч у л о н а\ о R о

где а >,, itj,, , п„ (.редине квадратические откл! вуют переменным х,. х.. Если случайные переменные в1ны. такчюр - I. то [П 13,11) сводится к следую

(П13 11)

(IIU 12)

Глава 14

АНАЛИЗ СВЧ СХЕМ

ВО ВРЕМЕННОЙ ОБЛАСТИ

В гл П рассмотрены методы анализа СВЧ цепей в частотной обла сти Как уже говорилось, методы анализа СВЧ пеней имеют особенно сти по двум причинам. Во-первых СВЧ устройства строятся на элемен тах как с распределенными, так и с сосредоточенными параметрами Во-аторых, для некоторых СВЧ компонентов обычным является описание с помощью S-параметров. При анализе во временной области методы исследования, используемые на низких частотах также видо изменяются с учетом упомянутых особенностей

в некоторых случаях становится необходимым анализ СВЧ схем во временной обпасти, К этим случаям относятся проектирование быст

9 Зак 22s4 257

родействующих цифровых интегральных микросхем, широкополосных радиолокационных систем и систем связи, а также исследование шз-денствия ЭМИ (электромагнитного излучения) на системы содержа щие линии передачи

Существует три основных метода анализа переходных процессов электронных схем - метод преобразования Лапласа, метод сопрошж дающей модели и метод переменных состояния. Методом преобразо ваний Лапласа анализируют линейные схемы или линейную часть об щей нелинейной схемы. Двумя другими методами можно анализировать и нелинейные схемы. Все три метода могут применяться на СВЧ Прежде чем приступить к краткому описанию этих методов, рассмотрим в следующем раздезе метод анализа зиний передачи во временной области

!4 1 АНАЛИЗ ПЕРЕХОДНЫХ ПРОЦЕССОВ ЛИНИИ ПЕРЕДАЧИ

Один из простейших методов анализа переходных процессов линии передачи основан на решении гиперболических дифференциальных урав нений в частных производных. Этот метод применяется для однородных линий передачи 11]. Его также можно распространить на исследова ние неоднородных линий передачи волноше сопротивление Z„ кото рых изменяется по длине 12!.

Система дифференциальных уравненпй в частных производных описывающих чинам передачи с волной Т-типа может быть записана в виде

д7 di

Oi до „ - С- \ Gv

(i4 1)

(142)

где L. R С и G - соответствен 1Ю погонные последовательные индук тивность и сопротивление, параллельные емкость и проводимость В линиях с малыми потерями /? и G могут считаться пренебрежимо ма лымн Дифференциальные уравнения (14.1) и (14.2) могут быть преоб раюваны в два обыкновенных дифференциальных уравнения Ч1 Мож но гюка!ать, что для однородной линии гюдсгановкой

(из)

dz d/-U LC уравнения (14 i) и (14 2) могут быть объеяиЕЕены

(14 4)

В литературе этот метод \ модели - прим. ред 258

? методом дискретной f.

Рнс !4.1. Семейства / и -характеристик

ниродиой линии пере-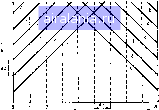

-1.1я ЛИНИИ без потерь уравнение (14 4) прншдится к виду

„,„ о „4 5,

те Vi определяется как v - iy L/C.

Соотношения (14.4) и (14.5) используются для анализа линии пере дачи ш временной области. Уравнение (14.3), на основании которого были получены (14,4) и (14.5), описывает семейство характеристиче-ких кривых в плоскости г I. Они называются прямыми характерис-шками (/-зависимостями или /-кривыми). В однородных линиях [средачи L и С не зависят от г и, следовательно, /-зависимости являются прямыми линиями (рис. 14.1). Общая дчина отрезка линии передачи разделяется на п равных частей Расстояние между соседними /-(ависимостями есть Д/ по оси времени и Дг по оси г Приращения Д/ и \г связаны между собой соотноцгением (14.3).

Второе семейство характеристических кривых для уравнении (14 1) ((14 2) имеет вид

dz,dt -\\ LC

(14 6)

14доль кривых, определяемых уравнением (14,6), г уменьшается с рос ЮМ /, и они называются обратными характеристическими кривыми или (-кривыми. Для однородных линий передачи эти й-кривые показаны иа рис. 14.1. Расстояние между соседними b кривыми обозначим через

\( и Дг вдоль осей ( и г соответственно Вдо1ь й-кривых из уравне-

тй (14 1) и (14.2) имеем

(14 7) 259