Порядок в которо.м корректируются элементы в процессе LU-фак торизации, также (аписывается в массив. Элементы корректируются для каждого ведущего элемента и порядок корректировки элементов записывается в массив Order, Каждый элемент массива Order указыва ет. что элемент массива А должен корректироваться в том же поряд ке в котором использовался в /.{У-факторизации.

Для рассмотренной ранее структуры матрицы массив Order содер жит следукнцие элементы:

Orders 16 144 i6 174 19 4 19 1855

Массив Pivot.st используется для определения начала операции кор рективки в массиве Order для каждого ведущего элемента, Если Pivotst (к) г. то для к-го ведущего элемента элементы для коррек тйровки передаются, начиная с Order (г) Так. в рассматриваемом слу чае массив Pivotst содержит следующую информацию: Pivot.st ] 5 9 \3

Теперь можно записать основной алгоритм LU факторизации с исполь зованием определенных ранее массивов:

• all i- 1 iv n -1 do begin

for all k-Urowst(i) lo Lcolst (i < 1) -I do A (k) = For all 3- Uolst(i) la Urowst(i) -1 do begin

For all kUrowst(i) to Lcoist ( +1}-1 h Ьецт

A (Order (/)) - \ (Order (/)) - \ (j) x A (k) end (for k) end (for J) end (Uv )

В ЭТОЙ процедуре выполняются только ненулевые операции и не требу ется просмотра списка от начала до конца.

Итак, рассмотрены прямое исключение и обратная подстановка для приведенной структуры данных. Для решения уравнения Ly b тре буются следующие ненулевые операции:

Решение у записывается через Ь. Для обратной подстановки, чтобы по лучить решение Ux = у ( с у, запоминаемым в Ь) дотжны выполняться следующие ненулевые операции:

b,-b,-n,,b.

Н(4)Й(4)-Л(19) й(5) Й(3)Й(3)-Л(16)Х 3(4) й(4)Й(4)-Л([7)х fi(4) Й(2)-Й(21 -Л(12) X Й(4) B(2).S(2) -Л(13) X S(2)

е(1)е(1)-Л(8)хй(3)

Н(1-«(1)-Л(9)хЙ(41

При обратной подстановке решение х также записывается только через Ь Алгоритм прямого исключения и обратной подстановки для рас смотренной структуры данных имеет вид

Прямое нсключени!; For all I I to f\ - 1 do beg n

B(i)-B(i),A([)

For all j = Uolst(i) to Urowst(i} -1 <>"

В (Rowcol (j)} - В (Rowcol (j)) -A (j) X В (i) end (for i) B(n)--=B(n).A(n) Обратная подстановка For ail i п -I step - i until I do begin

Fw all j-Urow5t(i) ti, LcoUt (i j \)d B(i)-B(i)-A(i)xB(Rowco4j)) end (tor it

В этой процедуре выполняются ненулевые операции а (юиск или сор тировка отсутствуют

Прямое исключение н обратная постановка для расчета чувстви тельностн. Как говорилось в подразд. i5.3.i, для определения чувстви тельности с помощью присоединенной схемы должна решаться транспонированная система уравнений В этом случае должны решаться уравнения (!5.32). Имеем

Ах (Ш)«х-~ иах--Ь (154!)

и следовательно решаем

Uy-..b относительно у и затем

их у

относительно х ;у равнения (1542) и (15 43) могутбыть переписаны в виде

(15 42)

(154i)

1 О О 1 О "1я "га

(15 44)

Процедура прямого исключения - обратной постановки легко может быть видоизменена для рассматриваемого случая. Алгоритм для этого случая имеет вид Прй«<.с исключение

/or all i I Iv П-] do begin

For (ill J L:row4t(0 lo Lcolst (i ; l -i do

B{Rowcol()) B(Rowoi(j)) A(j)xB (J end {for 11 /Обратная подстан>вка B(n) -В(п) Л(п) For nil i п I ч/е/ 1 u / / 1 i begin

For all i- Liolsldl to l;rowst(i)~- d

В 0) B(0-A(])xB(Ro.col(])) В (!) B{i) \Ui ena (for Ч

В ЭТОЙ Процедуре не выполняются нулевые операции и не осуществля ется просмотр всего списка.

15 4.4 З.ЛМЬ-ЧЛНИЯ !Ю ДЕЙСТВИЯМ С РАЭРЕЖРННЫМИ ПАТРИЦАМИ

paccmoipehhf дейсгвнн t рафсженн ходимо выиолинть только нену.чевые длите структуре данных можно избавиться от хр, на структура данных в форме двойного сь пользование треугольного индексирован* поиска при .Ь-факторизации и прямом

Несмотря на то, что создание таких структур данных и последующая перегруппировка требуют некоторых усилии, это выполняется тотько один раз, Прн оптимизации обычных схем может потребоваться проведение анализа сотни раз. Если схема большая, время и память, трейуеиые для этого, могут быть очень велики Прн нспользованви техники разреженных матриц перегруппировка строк и столбцов делается только один раз и массивы для треугольного индексирования создаются только один раз. При многократном повторении анализа труемое время резко снижается несмотря иа начальные расходы по перегруп-

1атрицами показывает, что необ-операцни и что при подходящей 1 нулевых элементов Предложе-иго ортогонального списка, Ис-г минимизировать время - обратной i

(15 45)

Часть IV ОПТИМИЗАЦИЯ

Глава 16

ВВЕДЕНИР В ОПТИМИЗАЦИЮ

В г1 1 были рассмотрены общие принииггы машинного проектирования. Как следует из схемы ггроцесса машинного проектирования, показанной на рис. 1.2, проектирование начинается с опредопения технических требованлн, предъявляемых к устройству, и определения первоначальной конфигурации устройства. Для анали.ча устройства разрабатывается его моде-чь, для чею нслольз>ется техника моделирования, рассмотренная в гл. 3-10. Характеристики скемы оцениваются с помощью методов анализа, описанных в гл- 11 -!5, Полученные в результате анализа характеристики сравниваются с 1аданными Если результаты сравнения неудовлетворительные, расчетные [1араметры схемы последова ельно изменяются но шределенной системе Последовательность анализа схемы, сравнение ее характеристик с заданными и изменение параметров повторяются до тех пор. гюка гге будут достигнуты оптимальные характернсгнкн Этот процесс, известный под на!ванием оптимизации, изображен иа счеме, пока,1анной на рис. 16,1

Имеется два подхода к изменению расчетных параметров К первому относятси градиентные методы, ко второму -методы прямого 1ю-иска. При градиентных методах для достижения измененного меюже-ства параметров используется информация о производных целевой функгщи относительно расчетных параметров. Эта информация получается в результате анализа чувствительности, производимого методами описанными в гл, 12, Поэтому в данном случае процесс оптимизации осуществляется, как показано на рис. 16,2. В противоположносгь это му при методах прямого поиска не используется информация о граднен

ЩВоначакона»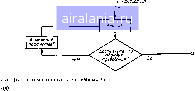

Псрбоночапьчая конфигурация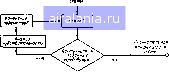

Рис- 16 2 CicMa процесса оптнм: сти .ыя вычисления градиентов

тах, и емраметры изменяются с помощью систематического поиска оп тимума.

Различные аспекты оптимизации хорошо отражены в литературе 11- 101. Наиболее важные особенности собраны в этой и двух последующих главах В этой главе приводятся основпые понятия, формулируются целевые функции, рассматриваются ограничения и изучаются од номерные методы поиска. В двух последующих главах рассматривают ся варианты многомерной оптимизации, осуществляемые методами пря мого поиска и градиентными методами

16 1 ОСНОВНЫЕ ПОНЯТИЯ и ОПРЕДЕЛЕНИЯ

Целевая функция и ограничения. Задачу оптимизации можно сфор мулировать как задачу минимизации скалярной целевой функции и (Ф). Функция и (Ф) есть функция ошибки, представляющая собой разность между достигнутыми на каждом шаге характеристиками и заданными требованиями. К примеру, в случае СВЧ транзисторного уси лителя целевая функция u (Ф) определяется по .заданным и достигнутым значениям коэффициента усиления, ширины полосы пропускания, а также возможно, входного сопротивления, уровня шума, динамического диапазона. Целевая функция u (Ф) называется также функцией Стоимости, критерием или индексом ошибки. Задача оптимизации обычно формулируется как задача минимизации u (Ф) Это не приводит к гготере общности, поскольку минимум функции u (Ф) соответствует максимуму функции - u (ф). Поэтому, заменяя знак u (Ф), любую задачу минимизации можно переформулировать как задачу максимизации, и наоборот С помощью Ф обозначено множество параметров проектирования, значения которых могут изменяться в процессе оптимизации. Обычно, чтобы решение было практически реализуемым, элементы Ф подчиняют некоторым ограничениям типа неравенств g (Ф) О и некоторым ограничениям типа равенств Л (ф) - 0. Для микрополосковых устройств элементы Ф - это длины и волновые сопротивления различных отрезков микрогюлосковых линий, сосредоточенные параметры и параметры активных устройств Различные ограничения возннка-