Часть И

МОДЕЛИРОВАНИЕ ЭЛЕМЕНТОВ СВЧ УСТРОЙСТВ

Глава 3

ЛИНИИ ПЕРЕДАЧИ

в диапа.чоне свч используется большое количество раэнообраз- ных линий передачи. к ним относятся коаксиальные 111, полосковые-(2-81, микрополосковые 191, щелевые (9), копланзрные f9i, связанные! полосковые 12] и связанные микрополосковые линии [9. эти линии передачи применяются наиболее часто. их поперечные сечения показаны на рнс. 3.] полуволноеые, четвертьволновые и 1/8-юлновые отрезки этих линий являются основными элементами большинства свч устройств. линии передачи характеризуются волновым сопротивлением и постоянной распространения (т. е. фазовой скоростью и постоянной затухания), которые определяются физическими napawerpaMMj структуры (как, например, геометрия поперечного сечения) н свойствами используемых диэлектрических н проводящих материалов.

в настоящей главе приведены приближенные формулы, пригодные лля расчета линий передачи этих типов. максимальная погрешность используемых приближений составляет 2...5 %. при моделировании свч устройств эти погрешности расчетных формул могут учитываться точно так же, как н погрешности, возникающие из-за неточности изготовления. тем не менее более точно рассчитать значения параметров можно с помощью численных методов анализа, рекомендации по которым также приводятся.

Микропапдсковая линия подвешенндй

t передачи, используемые в СВЧ устройс!

ах менее широко

кроме рассматриваемых в этой главе линий передачи имеются и 1)угне типы линий, применяемые менее широко. к ним относятся ми-ч[)о полос нова я линия с подвешенной подложкой [10 -111, перевернутая микрополоскован линия (121, диэлектрический волновод (161, «плавнн-1,1>вая» линия (141. н-образный волновод [15! и полосковый диэлектрн-Кский волновод il31. поперечные сечения этих типов линий показаны ла рис. 3.2, а их характеристики приведены в цитируемой литературе.

3 1. КОАКСИАЛЬНЫЕ ЛННИИ

основным типом волны, распространяющейся в коаксиальной ли-1ши, показанной на рис. 3,3а, является поперечная электромагнитная i волна. для любых не имеющих потерь линий с т-волной волновое сопротивление и фазовая скорость определяются выражениями

ZVLTc, (3.1)

уф 1/ктс, (3.2)

1де L W С погонные значения индуктивности и емкости линии (иа 1диии11у длины). используя формулы (3,1) и (3.2), можно выразить волновое сопротивление zu через фазовую скорость и погоннун!

2u-w(f* с).

(3.3)

Рис 3,1 Линии перслэчи, наиболе

i Г.ВЧ устройствах

. 3.3. Коаксиальная линия (н) и эквивалентная схема отрезка , л ллнкои Дг (б)

Если линия однородно заполнена диэлектриком с относительной диэлектрической проницаемостью с. то

vclVZ. (3.4)

где с - скорость распространения электромагнитной волны в свободном пространстве. В тех случаях, ко!да диэлектрик не заполняет линию полностью, соотношение (3.4) может быть aaiiHcaitu и виде

Vff-ri\?\. (3,5)

где са - эффективная диэлектрическая прошпаемость, связанная с емкостью линии выражением

tv,=C,C„ (3.6)

где С„ - погонная емкость линии, в которой диэлектриком является воздух.

Понятие эффективной диэлектрической проницаемости может применяться во всех случаях частично заполненных структур, в кшорых распространяется Т-волна (или близкая к Т-волне). Это 1юнятис ис-гюльзустся н микрополисных jirfsmh.-i и копланарных линиях, рассматриваемых далее. Для таких линий можно записать

(3.7) (3 8)

где Z% и Ре - шответственно волновое сопротивление и фазовая по-[ояццая для линий, в которых диэлектриком служит воздух.

Если учитывать потери, то для Т полны применимы соотноцицин

(3.9)

Z,V CJCZ\.

f3 Ю)

где h Й - погонные значения (на единицу длины) последовательного сопротивления и параллельной пpoвoдиюcти линии передачи.

Параметры R, L, О, С являются компонентами экупвале]тюй схемы отрезка линии передачи, показанной на ркс. 3.36. В выражеиияк (3.9), (3.10) у постоянная распространения (а - постоянная зату хания, р - фазовая постояилая) и е углоная чягтота. Если потери пренебрежимо малы, то уравнения (3.9), (3,10) совпадают с (3.1) и (:}.2) соответственно.

Параметры и у коаксиальной линии [1 ]. Погонные зиачеиня емкости и индуктивности коаксиа-чьной линии могут быть получены из aiiajfHaa статического поля:

С - 2ле./1п(&/а), (3.1!)

(3.12)

где р и 1l - диэлектрическая и магннтияя проницаемости среды; b внутренний радиус внешнего проводника; а - радаус внутреннего Проводника.

Используя (3.11), нплновое сопротивление лнкии с малыми потерн-L можно записать и виде

Д=Л-1п(6/а). (3.13)

il 1 --= v ц/е - волновое сопротивление среды заполнения. Для воздушного диэлектрика имеем

Zo=60 1n(&.o), (3.14)

4f Z<j в омах.

Потнное значение нас-тедовательного сопротивления рассчитывается 1IU формуле

де R, - поверХЕЮСПюе сопротивление проводника.

Погонная проводимость может быть рассчитана по формуле

G = 2ло/[п (Ыа) -=2лсо! 1g б/1п ф/а).

(3,[6>

где о - проводимость, а tg6 - тангенс угла потерь диэлектрика.

Коэффициенты затухания (Нп/м), определяемые значениями R и G. могут быть рассчитаны по слечукицим формулам;

в проводниках

a„p = ff.(2Zo), в диэлектрике

ад GZo/2 - сп!/2 - л 1/" Ig й/л„.

(3.17)

l3Jm

Суммарное затухание, выраженное в децибелах на метр, состац.1нст s:686 (а„„ : ад).

Как видно из формулы (3.15), значение R и, с1едовательно, затухание уменьшаются с возрастанием Ь и а . Увеличение этих размеров ограничивается возможностью возникновения волн высших типов. :" этой точки зрения наиболее опасной является низший тин Н-волны - ,»л1иа типа Н,,,. Критическая длина для волны этого типа определяется [ормулой

X,,,. 2п

i.3 Щ

I е. срез происходит при длине вол™, прнб.(!изительно равной длине вредней окружности.

: 2 ВОЛНОВОДЫ Щ

Широкое применение находят волноводы прямоугольного и кругло-м> поперечного сеяний. В данном разделе рассматриваются эти вол-поводы.

32 i ПРЯМОУГОЛЬНЫЕ ВОЛНОВОДЫ

Геометрия прямоугольного волновода и используемая система координат показаны на рнс. 3 4а В результате решения волнового равнения прн соответствующих граничных условиях можно получить

(3 20)

где у - постоянная распространения; k - toVpe - волновое число для диэлектрика, занимающего безграничное пространство; v - фазовая скорость а диэлектрике Критическое значение волнового числа А„р и критическая частота /„р определяются соотеюшением

(А,р)„„-2л (/„р)„

YlMf (32.)

где тип определяют тип волны „ или Е, „

Из (3 20) видно, что для / > /„р постоянная распространения является чисто мнимой величиной {у = jP) Фазовая скорость v и длина волны в волноводе Х, рассчитываются по значению р

Волна, распространяющаяся в волноводе, не является Т-волиой, и поэтому юлновое сопротивление не может быть определено однозначно Для таких структур волновое сопротивление Zg может быть определено одним из способов путем использования отношения напряжения к току или значения передаваемой мощности при заданном напряжении (или токе)

2о(и, )---7 . или ZoiW, 0-- . или ZiW, v) (3 22)

Для линий с Т-волной все эти определения идентичны, но для волноводов они приводят к трем различным значениям волнового сопротивления Все этн значения волнового сопротивления могут быть выражены через удельное волновое сопротивление Z„ определяемое отноше-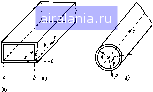

Рис 3 4 Прямоугольный (а) н круглый (б) вол

iilkm поперечных составлякедих электрического и магнитного полей дельное волновое сопротивление для Н-волны определяется формулой

2ИН)=-

(3 23)

для Е-волны

г, (Е) = Р/(ше) t) )/ 1 - Кр/о>) (324)

Полковое сопротивление для основного типа Н-волны в прямоугольном волноводе рассчитывается далее В формулах (3.22) v - макси-м:)льное напряжение между нижней и верхней стенками волновода, l I - суммарный Продольный ток в широкой стенке Все три значения, пределяемые формулами (3 22), могут быть выражены через удельное [юлновое сопротивление

Z,(v,l)Z,лЫ2a), (3 25)

2.(*.0-г.л»6;(8а), (3 26)

Z„(»,o)----Z,26,a (327)

Затухание в волноводе определяется главным образом неидеаль-постью проводников стенок волновода Для волн различных типов затухание волновода (дБ/м) может быть рассчитано по следующим ([юрмулам-

"п,)н„„ -

"Ч УТ=(/.р/) 1 7

Ч У1-(/кр/()

1+ -(/.р ) (3 28)

(1+/а)(/.р )+(1 -(/„ )) x

)/( + ")].("0) 0 29) Цт (Ыа) + п1/т (6/о)" + л]) (3 30)

»чУ1-(/кр П=

3 2.2 КРУГЛЫЕ ВОЛНОВОДЫ

Постоянная распространения и волновое сопротивление волново-la с круглым поперечным сечением (рис. 3 46) также определяются <рмулами (3 20), (3 23) и (3 24) соответственно Критическая частота / ,,р может быть рассчитана по значению критического волнового числа пр. которое для Е-водны определяется формулой

- нуль функции л (x), а - радиус волновода.

Для Н-волны имеем iKr)n I -р. ,1а, к Рп.1........нуль функции J„ {x).

(3 31)

(3 32)