ют т ток причине, что невозможно изготовить линию слшиком малой ширины а при слишком большой ширине линии могут возбуждаться волны высших ТИПОВ. Кроме того, имеются ограничения на раз.черы элементов с сосредоточенными параметрами и на параметры активных устройств. Спедует заметить, что значение U (Ф) может зависеть не только от параметров Ф, но и от некоторых других параметров не определяемых проектированием, таких как температура и т. д. Сле довательно эти параметры не входят в список параметров проектиро вания.

Параметры Ф определяют пространство Часть этого пространства Б котором выполняются все ограничения. на.швается допустимой об ластью R или проектируемым пространством R которое может быть определено как

R{Ф\gtФ};0. П1ф}- {)} (16 1)

Пространство R называется замкнутым, если все знаки неравенств нестрогие, шьрытым, если не разрешено ни одного знака равенства, в том числе и ггестрогого неравенства. Условия (16 1) определяют замкнутое прострапство- В пропессе оптимизации ищется оптимальное зна чение Ф внутри R

Глобальный минимум V (Ф). определяемый вектором Фтт на характеристической поверхности, порожденной U (Ф), таков что

6.ш.i((Фmml<f•MФ) (16.2)

для любого допчстимого Ф, не равного Ф,„,„ Ни один из общепринятых методой не гарантирует нахождения глобального минимума, с их по мощью вычисляется лишь локальный минимум, который может быть определен как

и(Ф„,.,,) тш и(Ф} 3)

ф. R

где R часть R в юкальнои окрестноеги Ф,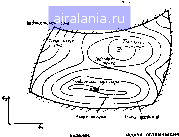

Рис 16 3 Т ополот чесяое предат 302

двумерной :

Рис !Ь4 Иллюстр пуклой ннер; н) и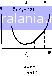

унимодальной (и) ifl функикн (,

Некоторые особенности, с которыми обычно сталкиваются в .зада чах оптимизации, проиллюстрированы на рнс. 16.3, где показаны ли НИИ уровня и в случае,когда вектор Ф двумерен. На этом рисунке по казаны допустимая и недопустимая области, линии уровня U, локаль ный и глобальный минимумы, седловзя точка н узкая долина. В сед ловой точке функция максимальна относительно изменений аргумента во одним направлениям и минимальна ~ ио другим.

Некоторые доЕюлннтельные свойства целевой функции (/ф) мо гут быть проиллюстрированы на одномерных функциях (7,как показа но иа рис. 16 4 Унимодальная функция (рис 16 4ii) может быть on ределена как функция, имеющая единственный оптимум в допустимой области R. Она может быть как непрерывной, так и разрывной. Строго выпуклая вниз функция рнс, 16 46) может быть определена как функ ция для которой для двух точек на ее поверхности Ф, Ф Ф,,

и{Ф, - ;.[Ф.-Ф,)<6 (Ф ) ; (/Ф.} (/(Ф,)

(16 41

где 0<Х< 1.Строго выпуклая вниз функция, умноженная на ( -I) называется строго выпуклой вверх функцией (рис. 16.4в). Если обе части неравенства (16.4) становятся равными, т. е, достижима линей нан интерполяция, то функция становится выпуклой и слово «строго» опускается (рис. Ш.4г), Термины «выпуклая» и «не выпуклая» исполь зуются также для области/? в пространстве Область R называется выпуклой, если для любых (Ф Ф,,) R все точки вида

- к{Ф Ф,) 0<Х<1

(165)

также принадлежат R. В противном случае говорят о невыпуклон об ласти. Выпуклые и невыпуклые области проиллюстрированы на рис 16.5.

Рнс 16 5 Выпукла

н невыпуклан (б) лолустнмые области

Разложение в ряд Тейлора. Другая общая идея, используемая в ме годах оптимизации - разложение в многомерный ряд Тейлора Раз ложение U (Ф + ДФ) может быть записано как

(/(ф+ДФ1-У(Ф)тУи1ДФ + (1 2)ДФНДФ+ (16 6)

ДФ1ДФ„ДФг ДФ»1

(16 71 (168)

Вектор VФ определяемый формулой (16.7). называется вектором при. ращения али, определяемый согласно (16.8). градиентным вектором. Гессиан Н в (16.6) - матрица размером (kxh), содержащая частные производные второго порядка записанные в внде

(169)

В точке минимума непрерывном функции с непрерывными частны ми производными 1-го порядка выполняются условия; 1) VU(a>mi„) -- О и 2) Н (Фтгп) - неотрицательно определенная матрица в сед-ювой точке (показанной на рис, 16,3} w - 0. ио гессиан не является ни положительно, ни отрицательно определенным. Такая точка

е собствен»!

1 Матрица называется положительно определенной, е. значения положительны, неотрицательно (соответственно отрицательно) опреде лёниой. еслн все ее собственные значения не отрниательпы (соответственно от-рнцательны) 304

соответствует относительному минимуму по одному множеству пере менных и относительному максимуму по остальным переменным

Сопряженные направления. Множество hi ;j векторов (или ианрав еиий) {Si} на.1ывается сопряженным относительно иочожительно оп ределенной матрицы Л или Л-соцряженным ести

S As - О

(16 10)

где А -симметрическая in л)-матрица. Это 1юиятие сопряженных иа правлений используется в нескольких методах оптимизации.

Если метод минимизации всегда позволяет опреде-шть минимум об щ,ей квадратичной формы за определенное ограниченное число опера ций и если предельное число операций непосредственно зависит от числа переменных л, то такой метод называют квадратично сходящим ся Если квадратичная функция

(/(Ф) -ФАФ b

(16 il)

минимизируется последовательно вдоль каждого направтения из мно жества п линейно-независимых 1-сопряженных направлений, то глобальный минимум U находится не более, чем за п шагов, отсчитыва ется от начальной точки.

162. ЦЕЛЕВЫЕ ФУНКЦИИ ОПТИМИЗАЦИИ СХЕМЫ

162 1 ОБЩИЕ- ОПРЕДЕЛЕНИЯ

Цель процесса оптимизации - уменьшить различие характеристик реализуемых в проектируемой схеме и заданных. Функция, колнчест венно оценивающая это различие, называется целевой. Для определе ния целевых функций процесса оптимизации разрабатываемой схемы оказывается полезным понятие взвешенной ошибки. Пусть действи тельная или комплексная функция Set) определяет требуемую характе ристику схемы, где ip - независимая переменная, например частота или время. Пусть также F (Ф, if) является характеристикой схемы на каждом шаге процесса оптимизации. Функ1шя F (Ф, if) называется также аппроксимирующей. Взвешенная функция ошибки может быть определена как

е{Ф p)a()lf(Ф fi S

(16 12)

гдеш {Щ - весовая функция. Роль весовой функции состоит в том. что бы увеличить или уменьшить различие F Ф, if) и S (if) для отдельных значений переменной if. Например, в случае полосового фильтра мо жет оказаться желательным уменьшить потери передачи в двух точках полосы Пропускания. Весовые функции, соответствующие этим значениям if следует установить достаточно большими

Чтобы выразить ошибку (или минимизируемое отклонение) как еди ную величину, используем норму взвешенной функции ошибки е (Ф чр) Дня непрерывной переменной if р-я норма определяется, как

f 1 с (Ф ЩЫ

1 рс

(!6 П)

Нслнже1) дискретная переменная то

\\\\,t\Jx\e (Ф)!"!" (61 \р (1614)

где с (Ф) е (Ф if,) - компонент вектора ошибки определяемого

е(Ф) с,(Ф),е,(Ф) е (Ф) (16 15)

I множество индексов соответствующих дискретным значениям в интервале (if,., чр) Если имеется п дискретных значений if то i i i(l,2, . . п) Используя (16.13) и (16.14). получаем два важных типа целевых функций. Они известны как средиестепенная аппроксимация /)-го порядка и минимаксная аппроксимация

162 2 СРЕДНЕСТЕПЕННДЯ АППРОКСИМАЦИЯ рг П0РЯДК4 В этом случае цепевая функция записывается как

и(Ф)- J г(Ф if)dif и пи в дискретном случае

(16 16)

(16 17)

Минимизация функции V {Ф), заданной формулами (16.16) или (16.17). известна как среднестепенная аппроксимация р-го порядка Минимум, полученный таким образом, соответствует наилучшему приближению в р-й норме функиии ошибки. При р 2 имеем общеизвестную целевую функцию наименьших квадратов. Обычная алгебраическая сумма ошибок не дает приемлемого значения целевой функции вследствие взаимной компенсации положительных и отрицательных ошибок. При р 2 норма, определенная в (16.13) или (16.14), называется евклидовой, поскольку измеряет расстояние в многомерном пространстве ошибок от начала координат до конца вектора е (Ф), заданного формулами (16.15). В случае наименьших квадратов целевая функция имеет вид

/(ф) = 1в((Ф)р.

(16 18)

где п - число точек в выборке if Функция U (Ф) может быть выражена через вектор ошибки е (Ф)

и{Ф) ...::[с(Ф)1Ме(Ф) и Градиент U (Ф) равен

и - 2J е (Ф) где J - (ft X*) матрица Якоби имеющая вид

(16 19) (16 20)

Матрица Якоби может быть также исполь,ювана при разложении функ ции ошибки е (Ф) в ряд Тейлора с точностью до малых второго поряд

е(Ф-г Дф)я;е(Ф) \ МФ

(16 22)

Если же /) > 2, то больший вес автоматически придается большим ошибкам. Рассмотрим, например, целевую функцию с двумя компо иеитами вектора ошибки 1 н e-i 2. Для р ------ 6 и одинаковых ве

сов получаем

и.--(У + 2У - (65)1 >л2

(16 23)

Если теперь уменьшим е, на 1 (т. е. - 0), то обнаружим, что U все еще равно двум. С другой стороны, если уменьшить на единицу (т е. принять - i), то целевая функция немедленно уменьшится с двух до 2 x !. Дальнейшее увеличение значения р еще более усн лит преимущественное рассмотрение больших ошибок.

16.2.3 МИНИМАКСНАЯ АППРОКСИМАЦИЯ

Если в (1Й.13) или (16.14) р оо, поведение целевой функции определяется дпя достаточно гладких функций как

шах 1(Ф if) hm

«(Ф til dif

а для дискретного с-1учая как

шахе (Ф)-11т{2\,<Ф)1} " Ё»

(16 24)

(16 25)