микрополосковой линии При малых значениях Wlh полученные результаты оказываются очень неточными, так как значения Wh и s/ft малы В работе [441 показано, что использование лучших формул синтеза одиночной микрополосковой линии позволяет уменьшить погрешность до значений, меньших 3 % для е 9,6, 0,1 W/h 2 и 0,05 < s/ft < 1 [441

Значения Wlh и s/A для связанных микрополосковых линий могут быть получены из совместного решения следующих уравнений

2W-g-1 1

.-Л Arch f

(3 120)

для е, sje. Р 121а) - J-Archfl+2-?j для с,>в.

(3 1216)

(3 122) (3 123)

(Т - отнои1ения, соответствующие волновым сопротивлениям 2пг2 и Zy„;2 для одиночной линии, они мог\т быть гюлучены из форм\л синтеза (3 53)

Приближенное совместное решение уравнений (3 120) и (3 121) может быть получено, если пренебречь вторым членом в (3 121) Затем значение s/i можег быть найдено по формуле

(3 124)

(3 125)

Значение s/Л. полученное из (3 124). может быть использовано как начальное в процессе оптимизации при решении уравнений (3 120) и (3 121)

Характеристики различных линий передачи, рассмотренных в этом разделе, необходимы для моделирования секций на этих линиях, используемых в различных СВЧ устройствах 56

Глава 4

ЧУВСТВИТЕЛЬНОСТЬ ЛИНИЙ ПЕРЕДАЧИ

4 1 ВВЕДЕНИЕ

И гл 3 исследованы характеристики различных линий передачи и1ме этого, необходимо определить влияние изменения параметров 1 чарактеристики линий передачи, используемых в различных уст-ч1ствах Анализ, позволякщий определить это влияние, называется и i,ih30m чувствительности

4 1 1 ОПРЕДЕЛЕНИЯ

Чувствительность функции F к параметру х определяется как

(4 1а)

(4 16)

В соответствии с этими формулами чувствительность 5 можно 1П)еделить отношением относительного приращения функции F к от-сительному приращению параметра х прн условии, что этн прираще-н1я достаточно малы (стремятся к нулю) В литературе Sf иногда на-ивается нормированной чувствительностью в отличие от ненормнро-к.и[Ной чувствительности, которая определяется просто как частная )оизводная dFldx Если FecTb функция некоторых параметров xj, xg, , , Хп. то эти параметры могут быть представлены вектором, а век-пр градиента F определяется столбцом, состоящим из различных про-инодных dFldXu dFldx, . дРдх„

dF дх, OF v.

(4 2)

iii lb VF эквивалентная ненормированная чувствительность, oiipe-<< книая выЕпе

1 i ПРИМКПЬНИЬ АНАЛИЗА 4i ВСТВИТЕЛЬНОСТИ

При разработке устройств чувствительность (нли градиент) оцени-1-ч1н в основном в двух случаях при анализе допустимых отклонений и процессе оптимизации Анализ допустимых отклонений может инываться на определении чувствительности, а информация о гра-i и iiic необходима при осуществлении ряда методов оптимизации

Анализ допустимых отклонений. Необходимость анализа допустимых отклонений физических параметров СВЧ устройств и параметров материалов вызвана ограниченными возможностями технологии изготовления и (или) погрешностями измерения Отклонения этих параметров от номинальных значений приведут к ухудшению технических характеристик разработанного устройства В процессе анализа необходимо установить значения допустимых отклонений, при которых характеристики устройства удовлетворяли бы заданным требованиям. С другой стороны, могут быть установлены необходимые требования к технологии для успешного изготовления разработанного устройства Анализ чувствительности является лучшим способом исследования возможностей компромисса между техническими характеристиками устройства и допустимыми отклонениями его физических параметров Наряду с отклонениями параметров следует учитывать, что модели некоторых компонентов, на которых базируется конструкция, могут быть приближенными Погрешности в значении параметров модели могут иметь тот же порядок, что и допуски на физические параметры С этими погрешностями модели можно поступать точно так же, как и с допустимыми отклонениями П1 Ухудшение характеристик устройств, обусловленное допусками на различные конструктивные параметры, будет рассматриваться в гл 13 В настоящей главе определяются отклонения характеристик линий передачи, возникающие из-за неточности их изготовления и разброса параметров материала

Использование расчета чувствительности при оптимизации. Некоторые методы оптимизации характеристик схем рассматриваются в гл 16-18 В обычных алгоритмах оптимизации значения конструктивных параметров изменяются до тех пор, пока достигается минимум «ошибки» или «целевой функции» Градиент функции используется для определения необходимого изменения значений параметров на (/ + 1)-й итерации, увеличение (или уменьшение) которых по сравнению с /-й итерацией !авнсит от градиента

Градиенты характеристик линий передачи могут быть получены из чувствительности, рассматриваемой в настоящем разделе

4 1 i анализ допусков линий передачи

Отрезки линий передачи являются основными элементами при построении СВЧ устройств Поэтому весьма важно исследовать чувствительность линий передачи к изменению конструктивных параметров С помощью анализа чувствительности исследуются отклонения характеристик линий передачи в наихудшем случае

Формулы для изменения характеристик линий передачи выводятся далее Находится также изменение волнового сопротивления Д2 в функции коэффициента стоячей волны по напряжению (КСВ) стыка исследуемой линии с линией, имеющей точные размеры. Приводится также изменение фазовой скорости v в линии передачи.

Изменение характеристик линии передачи. Изменение волноаогс сопротивления линии передачи Л2 согласно формуле (4.1а) связаш

шмтимым отклонением AS параиетра в соотношением

/„ bojihoboe сопротивление при лв 0. Если волновое сопро- кнне является функцией нескольких независимых переменных , 1Деп J, 2, , Л, то суммарное изменение Z может быть за пицц в виде

7- -i

(4 4)

";;1",;.L°™™"™"\V*" приводит к увеличению значении AZ Маи-"тношёния - """"У""™ :У-»< быть найдено из

(4 5а)

аналогично максимал пшсать как

ьное изменение фазовой скорости (Ло)„

"» (4 56)

У Павнення (4 5) позволяют определить максимальные изменения z. и " в функции допустимых отклонений "

„„rj,T"°-°""\" задача - определение требований к технологии ипотовления для обеспечения допустимых изменений характеристик .."1ии передачи - рассматривается далее рчктеристик

Определение требуемой точности изготовления. Допустиж>е откло-.»ие параметра S, при изготовлении ДВ„, при котором значение ТавГнГ " """""" «"ь "айДенС из дует

I is,.

(4.6)

Уравнение (4 6) справедчиво, когда его правая часть положительна 11 противном случае требуемое значение az не может быть обестено

\::.s::Tb "Т"""- ™руого знат.

мнение ДВ„ может быть найдено нз уравнения

I дв„

(4 7)

.nslZ ILT"""*" (и по дг, и по 4.), то должно

гь выбрано минимальное из двух значений b„.

Приведенный анализ устанавливает связь между точностыс изго товлення н техкическнмн характеристиками. Могут быть также установлены требования к технологии изготовления для получения задан ных технических характеристик линий передачи.

Приведенные здесь формулы имеют общий характер и пpиeнимы к любым типам линий передачи. Далее будут представлены подробные расчеты для коаксиальной линии, прямоугольного волновода, пслоско-1 вой линии, миьрополосковой .1ииии, копланарных линий, связанных полосковых и микрополосковых линий.

Оценка чувствительности. Так как чувствительность определяется; частными производными zg и и по соответствующим параметрам, то формула чувствительности может быть получена, если известны выражения для zo и и в замкнутой форме. Для этой цели используются вы- ражения в замкнутой форме для линий передачи, приведенные е гл. 3. Если допуски на изготовление меньше погрешности используемых выражений в замкнутой форме, то для повышения точности могут при-, меняться численные методы определения параметров линий передачи. I В планарных линиях передачи, используемых в интегральных схемах, СВЧ, чувствите1ьность характеристик линии передачи к изменению, толщины металлизированного слоя, как правило, невелика. Поэтому в разд 4 4-4.6 этой чувствительностью пренебрегают

4 г КОАКСИАЛЬНЫЕ линии

Выражение для чувствительности коаксиальной линии мож1т быть получено из формулы волнового сопротивления (3 13) и определе! чувствительности (4.1)

4.i tpifiyemafl точность нак w рмрутреннего проводника i льиой лнн!ри, необхо,

(здесь zo - в омах).

(4 8) (4 9)

1

I 0,10

т бй м

рис. 4 i. чувствительность волнового рис 4 2 максимальное изменен!

сопротивления н фазовой скорости волиопого сопротивления коаксиал

коаксиальной линии fioh линии, вызванное влиянием д.

пусков изготовления (0=1,45 чм)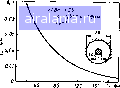

рафик чув.;твительности приве it-h на рис. 4.1, Эта кривая и

!авнение (4.5) использованы 11я построения графика мзкси-1ального изменения волнового опротнвления, который приве \чп на рис. 4.2. Эта кривая ха )актеризует также изменение

<СВН от стыка рассматриваемой линии, имеющей отклонение, с деальной линией (без отклонений) в наихудшем случае. Эти отра кения пропорциональны д/ц. Допуск (или точность при изготовле 1ни) на размер а (или &) для допустимого значения az и другие до lyckh могут быть найдены из формулы (4.6). График требуемой точ иости изготовления для типичного случая приведен на рис 4 3

13 волноводы

Прямоугольные волноводы. Для прямоугольных волноводов на более употребительными параметрами являются фазовая постоянная (i и критическая частота /„р. определяемые формулами (3.20) и (3.21) .оответственно Чувствительность этих характеристик по отношению к параметрам а & и ег определяется следующими формулами-

(4 10) (4 и) (4 12) (4 13) (4 14) (4 15)

о в волноводе трехсантиметрового диапазона {а --22,9 мм. 6 10,1бмм)5"р О а S"" - - 1 Графики чув-1Вительности относительно размера а в функции частоты приведены .1рис.4.4. Прн анализе схем иногда оказываются необходимыми и яру