ствует спектру частот, используемых в аппаратуре ЦТС. Верхняя граница /в активной ширины спектра определяется длительностью наиболее коротких информационных импульсов, циркулирующих в ЦТС, и длительностью их фронтов. Пусть частота задающего тактового генератора ЦТС равна ft, тогда за tu можно принять значение л; \/2fi. Если к тому же отношение длительности фронтов импульсов iф к длительности 4 удовлетворяет неравенству WH0,25, то /в0,75Ди=1,5 /т [64]. Минимальная длина волны, соответствующая частоте /в, равна в этом случае Х=2-10*-1 т. Эту величину в первом приближении и можно считать расстоянием до границы ближней зоны. Так, например, ЦТС среднего быстродействия с тактовой частотой 2 МГц находится в ближней зоне источника помех с активной шириной спектра до 2 МГц, если последний отстоит от ЦТС не далее чем за 100 м.

Воздействие источника внешних помех на приемник

Под приемником ниже подразумевается либо подлежащее защите от помех изделие, либо специальный измеритель помех.

Представим источник и приемник двухполюсниками. Провода и части конструкции, которые можно отождествить с полюсами, обладают некоторыми собственными (по отношению к земле) и взаимными (по отношению друг к другу) емкостями. Обозначим полюсы источника и приемника буквами а, b и т, п соответственно. Тогда наиболее общая эквивалентная схема емкостных связей имеет вид, показанный на рис. 3.7, а, где Zi - внутреннее сопротивление источника, 22 - входное сопротивление приемника.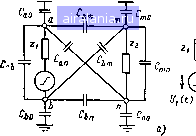

Рис. 3.7. Эквивалентная схема емкостных связей между незаземлен-ными {а) и заземленными (б) источником и приемником внешних помех

Если схема связей симметрична, т. е. СьтСыг, Сат = = Сап, Спо=Сто, Сао=Сьо, ТО потенциалы точек т и h одинаковы и, следовательно, восприятия приемником сигнала помехи не происходит. На практике, как правило, точки п и 6 соединены с землей. При этом схема связей становится несимметричной и на входе приемника появляется напряжение помехи U2 (рис. 3.7,6).

Будем называть идеальными источник, если его внутреннее сопротивление равно нулю, и приемник, если его входное сопротивление бесконечно велико. Если источник и приемник идеальны, то сигнал, наведенный источником на вход приемника, по форме аналогичен сигналу на выходе источника, а по амплитуде он меньше в (C2 + Ci2)/Ci2 раз:

u,{t) = UAt)c,i/iC, + c,. (3.36)

в неидеальной схеме форма принятого сигнала может существенно отличаться от формы сигнала источника.

Весьма часто входную цепь приемника можно представить схемой замещения, состоящей из параллельно соединенных резистора R2 и конденсатора Сз. Предположим, что выходное сопротивление источника активно, т. е. Zi=Ri. Отыщем для такого случая функцию U2(t), полагая сигнал на источнике скачкообразным [Ui{t) =E-l(t)] или синусоидальным [Ui{t) =Е sin tilt].

Из схемы на рис. 3,7, б после несложных преобразований следует (в изображениях по Карсону)

ip) = и, (р) pRC,, [pR.RC + С,, + Сз) (С, + С,,) - Cjj] +

+PIR2 {С2 + + Q + 1 (Q + Qa)! + 1} (3.37)

Как правило, емкость Ci2<Ci, С2, поэтому членом C2i2 можно пренебречь.

Если сигнал на источнике представляет собой скачок, то Ui(p)=E и (3.27) преобразуется к виду

и[р) = Е-( - Р---

где Т2 = ?2(С2 + С12 + Сз); Tl=i?l(Ci+Ci2).

Соответствующий оригинал

f/a (О = Е (е-/- - e-"). (3.38)

Та -

Из (3.38) следует, то переходная функция представляет собой импульс, сформированный из двух экспонент с постоянными времени xi и Т2.

Вольт-секундная площадь импульса

V,= Ju2(t)dt = ER,C,2. (3.39)

Для нахождения амплитуд импульса U2max достаточно продифференцировать и приравнять нулю выражение (3.38). Проделав это, получим

U2n,a. = ER,C,,/T,k, (3.40)

где k= (ххуг/--г).

Если T2/tic», то k-l. Если T2/ti-0, то &->Ti/t2.

Эквивалентная длительность импульса (длительность прямоугольного импульса, имеющего такую же амплитуду и вольт-секундную площадь) равна:

H = Wma. = b2. (3.41)

Длительность переднего фронта импульса в первом приближении можно принять равной:

Tl, если Ti<T2; 2)

Тз, если Тз < Tj.

Из (3.39) - (3.41) следует, что для оценки влияния источника на приемник необходимо знать значения емкостей Сь Сг и Ci2.

Частичные емкости в системе двух тел и проводящей поверхности

Полюсы а и m на рис. 3.7, б условно назовем антеннами источника и приемника. Их можно рассматривать как системы заряженных тел вблизи проводящей поверхности. Задача определения значений частичных емкостей в такой системе может быть сведена к менее сложной задаче определения значений потенциальных коэффициентов.

Действительно, пусть заряды на телах 1 и 2 (рис. 3.8) равны <7i и <72 соответственно. Тогда потенциалы тел ф1 и Ф2 связаны с зарядами формулами Максвелла [65]

Ф1 = «А + адг; 1 (3 43)

Ф2 = «1291 + «292- 1

Здесь ai, 02 - собственные потенциальные коэффициенты, ai2 - взаимный потенциальный коэффициент.