1863 В7

1864 С8

1865 F5

1866 F5

1867 СГР2012 186А ГРА7618

186£1 F1 186Е ЗГР i86F С26618

1872 AF

1873 С37718

1876 til

1877 IPI

1878 7A

1879 C9 0000

гПРОВЕРКА ПОКАЗАТЕЛЯ СТЕПЕНИ НА НОЛЬ • .

ORA А !ПРОЯВЛЕНИЕ ПОКАЗАТЕЛЯ

RZ гЕСЛИ П0КАЗАТЕЛЬ=0

PUSH PSU гСОХРАНЕНИЕ ПОКАЗАТЕЛЯ

г«ИКЛ УМНОЖЕНИЯ АРГУМЕНТА НА ЧАСТИЧНОЕ ПРОИЗВЕДЕНИЕ

ЦИКЛ: PUSH PSU гСОХРАНЕНИЕ СЧЕТЧИКА «ИКЛОВ

CALL УДПЗЗ г(В,С)-АДРЕС ПРОИЗВЕДЕНИЯ JC ПЕР1 гЕСЛИ ОШИБКА ПОРЯДКА

гПРОВЕРКА КОНЦА ЦИКЛА

гВОССТАНОВЛЕНИЕ СЧЕТЧИКА ЦИКЛОВ

POP DCR JNZ XRA JMP

PSU A

ЦИКЛ A

ПЕР2

гЗАЦИКЛИВАНИЕ гС¥=0

гВОССТАНОВЛЕНИЕ РЕГИСТРОВ

nEPls ПЕР2:

POP POP MOV RET END

D г БАЛАНС СТЕКА

D гВОССТАНОВЛЕНИЕ ПОКАЗАТЕЛЯ

AtD г(А)-ПОКАЗАТЕЛЬ СТЕПЕНИ гСУ=1.ЕСЛИ ОШИБКА

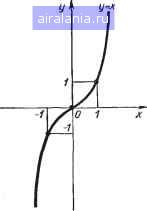Рис. 4.3. Графики степенной функции

Такой подход уменьшает затраты памяти, но существенно увеличивает время решения, особенно при больших значениях п.

Число операций умножения при вычислении степенной функции можно уменьшить, если разложить показатель я на множители, кратные двум [1, 48]. Так, для « = = 2k или n = 2k имеем соответственно х" = {xf или х" = {xY • X, т. е. для вычисления х" требуется не более k или {k -{- 1) операций умножения. Аналогичный подход

можно применить для вычисления и т. д. Например, вычисление х=[{х xff требует всего трех операций умножения вместо семи. В общем случае целочисленный показатель п можно представить в виде двоичного полинома по схеме Горнера: и = (...((О + а;б ,) • 2 + + аА 2)-2+ ai)-2 + 00. Тогда метод экономичного вычисления х" определяется выражением

х"(...Цх° х"-у . х-у .... х") • х", (4.8)

где х° = х, если а,- = 1, и х°- 1, если щ = О, г = О, 1,2, k- 1. Вычисление выражения (4.8) начинается с анализа старших двоичных разрядов показателя п. Если ak- \ = 1, вычисляется частичная степень {х° • xf = х; если следующая цифра ak-2 - 1, полученная степень умножается на аргумент и возводится в квадрат: {х-х) -х; если же о;д, 2 = 0, сразу следует возведение в квадрат: (x) = х и т. д. Например, вычисление xJ в соответствии с методом (4.8) имеет вид (7io= 11 Ь):((л;) • л;) • =Применение метода (4.8) требует не более [log2n] операций возведения в квадрат и не более такого же количества операций умножения на х.

Программа СТЕПА вычисляет степенную функцию по методу (4.8):

1890 ORG 1890Н

1220 УДПЗЗ SET 1220Н

0180 ЕДПЗ SET 180Н

СТЕПА:

;««*»»«»х««х»»»)(»к»хх«»»«х«»»)(»»»»»»»*«»»««»хк«»х«»)(»»)(« гПОДПГОГГАММА ВЫЧИСЛЕНИЯ СТЕПЕНИ У(У)=ХххЫ (N ( 256). гВХОДНЫЕ ПАРАМЕТРЫ:(HtL)-АДРЕС АРГУМЕНТА Х.ПРЕДСТАВЛЕН-;НОГО В ФОРМАТЕ 3-БАЙТНОГО ДВОИЧНОГО *СЛА В ДОПОЛНИ-

гтЕльном КОДЕ С плавающей запятой.(А)-показатель степени

;В ФОРМАТЕ «ЕЛОЧИСЛЕННОГО ДВОИЧНОГО БЕЗЗНАКОВОГО ЧИСЛА. ?(В.С)-АДРЕС СТЕПЕНИ.выходной ПАРАМЕТР!СУ=1-ПРИЗИАК ПЕ-гРЕПОЛНЕНИЯ ИЛИ АНТИПЕРЕПОЛНЕНИЯ ПОРЯДКА СТЕПЕНИ.ИСПОЛЬ-, гЗУЮТСЯ ВСЕ РЕГИСТРЫ.СОХРАНЯЮТСЯ (H.L.). (В.С) . (А) .ГЛУБИНА

;СТЕКА-24.ИСПОЛЬЗУЮТСЯ ПОДПРОГРАММЫ!хУДПЗЗх,хКОМЗх,хОБНЗ ? ХУДФ17х г ХНМАН2Х,ХДОПВХ.хДОПДх,хузЗБх,хУ24Ах,хЕДПЗх. ;0«ЕНКА:ДЛИНА-48 БАЙТ (+241 БАЙТ ПОДПРОГРАММ).ВРЕМЯ-НЕ ;Б0ЛЕЕ (142+4285x8) ТАКТОВ (С УЧЕ\т ПОДПРОГРАММ). ;ххххххххххххххххххххххххххххххххххххххххххххххххххххххх гЗАНЕСЕНИЕ "1" В ФОРМЕ С ПЛАВАЮЩЕЙ ЗАПЯТОЙ В РЕЗУЛЬТАТ 1890 СВ8001 CALL. ЕДПЗ

гПРОВЕРКА ПОКАЗАТЕЛЯ СТЕПЕНИ НА НОЛЬ

1893 В7 ORA А J ПРОЯВЛЕНИЕ ПОКАЗАТЕЛЯ

1894 С8 RZ гЕСЛИ П0КАЗАТЕЛЬ=0

1895 FS PUSH PSW гСОХРАНЕНИЕ ПОКАЗАТЕЛЯ

1.87

Программа выполняет анализ очередной двоичной цифры показателя степени путем сдвига его влево. При этом значение цифры совпадает с признаком переноса: CY =ai. Сопоставляя программы СТЕП и СТЕПА, можно увидеть, что последняя требует несколько больших затрат памяти, но зато при больших п(п>16) она вычисляет степенную функцию быстрее, чем программа СТЕП. Заметим, что в обеих программах расчет времени их работы дан для наихудшего случая, когда все двоичные цифры показателя степени равны единице. Тестовые данные для обеих программ приведены в табл. 4.2.

Табл. 4.2. Тестовые данные у =J("