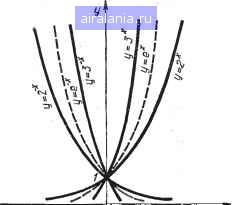Рис. 4.6. Графики показательной функции

Для вычисления экспоненты на более широком интервале значений аргумента значение х можно представить в виде x = n-\-z, где п - целая часть аргумента; г - дробная. Тогда вычисление сводится к вычислению

на интервале (-1, 1), а также степенной функции е;; (2,718)"..

4.8. тригонометрические функции

Тригонометрические функции определяют трансцендентную зависимость, т. е. зависимость, которая не может быть точно выражена в виде конечного алгебраического уравнения, между угловыми а и прямоугольными {х, у) координатами некоторой точки С окружности единичного радиуса х-\-у = 1 (рис. 4.7). Ордината точки определяет функцию синуса у = sin а, абсцисса - функцию косинуса X = cos а, отношение координат у/х, или, что то же самое, величина отрезка касательной BD,- функцию тангенса tg а = sin a/cos а, обратное отношение координат х/у, или величина отрезка касательной FD,- функцию котангенса ctg а = cos a/sin а (на рис. 4.7 а = 45° и tg45°= ctg45°= 1). Аналогично тригонометрические функции определяются для любого угла а, отличающегося от острого угла а. Аргумент а тригонометрической функции представляет собой действительное число, которое можно понимать не только как величину централь-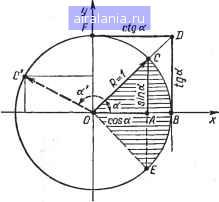

Рис. 4.7. График интерпретации определений тригонометрических функций

НОГО угла ИЛИ длины дуги ВС, но и как площадь сектора круга с углом 2а: площадь равна 0,5? • 2а = а (на рис. 4.7 сектор заштрихован). Именно поэтому тригонометрические функции иногда называют круговыми [25, 70].

Функции y = s\nx и у = cos X определены на всем множестве действительных чисел, но область их значений ограниченна: г/е [-1,1]. Обе функции являются периодическими с периодом Т= 2л, функция sin х - нечетная, а cosa: - четная. Графики функций sin л: и cosx пересекаются с осью абсцисс соответственно в точках х = = /гк и X = п/2 кл и имеют экстремумы (максимум или минимум) в точках х = л/2-}-лп и л: = /гл, k = 0, ±1, ±2, ... (рис. 4.8, а). Функции y = igx и y - ctgx определены для всех х, кроме х = п/2 + kn для тангенса и х = кл для котангенса, в которых соответственно cosx и sinx обращаются в нуль. Обе функции периодические с периодом Г = п, нечетные и не ограниченные в области своих значений. Графики функций tgx и cigx пересекаются с осью абсцисс соответственно в точках x = kn я X - л/2 4- kn (рис. 4.8, б, в).

Функция у = sin л; разлагается в ряд Тейлора:

sinx= -

5! 71 "г о

(4.10)

С радиусом сходимости R=oo. Определим количество членов ряда (4.10), необходимое при вычислении функции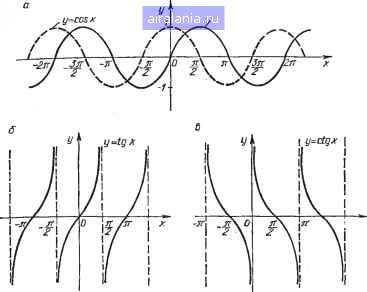

\27f л

Рис. 4.8. Графики тригонометрических функций: а -синуса и косинуса; 6 -тангенса; в-котангенса

С ТОЧНОСТЬЮ ДО четырех значащих десятичных цифр, т. е. А = 0,5- 10~, для диапазона аргумента xe[-п/4, п/4]. Подставляя в ряд (4.10) значение л: = п/4« 0,7854, найдем, что отбрасывание члена x/Tl вносит погрешность 0,3710" <: А. Поэтому для вычисления функции у = = sinx в заданном диапазоне и с требуемой точностью достаточно взять (с запасом) первые 4 члена ряда (4.10) с коэффициентами: 1/1! = 1, -1/3! =-0,1667, 1/51 = = 0,8333-10-2 и -1/7! =-0,1984-10-1 Этот метод вычисления синуса положен в основу программы СИН:

1А30 18Е0 1931 0068

ORG 1А30Н ПОЛИН set 18Е0Н ВУФЕР set 1931Н

пиз set овен

СИН:

гПОДПРОГРАНМА ВЫЧИСЛЕНИЯ СИНУСА ОСТРОГО УГЛА У= sin Хт гГДЕ (-"пи"/4 <= X <= +"ПИ"/4).

{ВХОДНЫЕ ПАРАМЕТРЫ:(НгЕ)-АДРЕС АРГУМЕНТА,ПРЕДСТАВЛЯЕМОГО ?Б ФОРМЕ ,3-БАИТНОГО ДВОИЧНОГО ЧИСЛА В ДОПОЛНИТЕЛЬНОМ

{КОДЕ С плавающей запятой,(с,Е)-адрес ФУНКЦИИ,ПРЕДСТАБ-