

|
|
Главная -> Современная электроника 0 1 2 3 4 5 6 7 8 9 [10] 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 Пример 3. Сумматор. Сумматор, в отличие от полусумматора, должен воспринимать не два, а три входных сигнала: два слагаемых и сигнал переноса с предыдущего разряда. а) 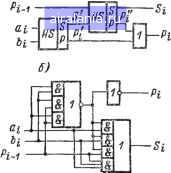 at bi Pi-1 Еис. 14. Схемы сумматоров В Принципе сумматор можно построить из двух полусумматоров и одной цепи «ИЛИ» так, как это показано на рис. 14, а (условное обозначение полусумматора соответствует ГОСТ 2.743-72). Первый полусумматор производит ело- Таблица 7 жение чисел с; и и вырабатывает промежуточные сигналы Si и Рг. Второй полусумматор складывает сумму 5, и перенос с предыдущего разряда На выходе второго полусумматора формируются сигналы суммы Sj и второго промежуточного переноса Р/. Общий сигнал переноса Pi представляет собой дизъюнкцию сигналов Pi и Pi". Схему сумматора можно также построить, если подходить к нему, как к единому узлу, воспринимающему три входных сигнала. Из таблицы функционирования сумматора (табл. 7) видно, что функция переноса {Рг) совпадает с функцией, реализуемой пороговой ячейкой, которая была рассмотрена в первом примере настоя-
щего параграфа. Поэтому можем сразу написать полученное ранее минимизированное выражение: Pi = a,Pi i + aA + biPi-i. Выражения для суммы (Si), записанное исходя из табл. 7, Не поддается упрощению: 5г = afii Pii + ai Д- 1 + Pi i + afiiPix. Ha рис. 14,6 и в показаны примеры сумматоров, построенных на элементах «И-ИЛИ-НЕ» и «ИЛИ-НЕ». 9. Схемы сравнения кодов В настоящем параграфе мы рассмотрим примеры построения более сложных комбинационных логических цепей, а именно схем сравнения кодов. Подобные схемы довольно часто встречаются в промышленных цифровых приборах и измерительных системах и служат, например, для определения соответствия измеряемого параметра заданному уровню. Схемы сравнения кодов можно разделить на две группы: схемы, выявляющие совпадение кодов (ВСК), и схемы, выявляющие большее число (ВБЧ). Схемы, выявляющие совпадение кодов (схемы ВСК), должны обеспечивать выходной сигнал, равный единице, только в случае полного совпадения сравниваемых кодов. Пусть сравниваются коды aia2a3..., а-п и ЬфгЬз- ., Ьп- Совпадение кодов означает равенство чисел во всех разрядах: ai = bi; a2 = b2; ab; . . . ; ab. Сравнивая два одноразрядных кода, можно, не составляя таблицы функционирования, записать логическую функцию схемы век, основываясь на том, что для совпадения необходимо, чтобы оба кода были равны единице или оба были равны нулю: Поскольку функция Ri = aibi-\-aibi позволяет выявлять совпадения одноразрядных двоичных кодов, ее называют функцией логической равнозначности. Соответственно функция Ri = aibi + + aibi носит название логической неравнозначности, или суммы по модулю два (такое выражение реализуется для суммы в полусумматоре), или функции «исключающее ИЛИ» (единица на выходе будет тогда, когда присутствует единица на одном или другом входе, но не на обоих входах одновременно). Функция, которую должна реализовать схема ВСК для многоразрядных кодов, может быть записана как конъюнкция функций совпадения всех разрядов сравниваемых кодов: Проинвертировав правую часть равенства, получаем другой вид выражения для R: R==aibi + aibi + a2b + a2b2+ - . + c„fe„ + «A- Выражение (6) в ряде случаев более удобно, чем (5), так как его реализация приводит к более простым логическим цепям. На рис. 15 показаны схемы ВСК на элементах «НЕ-ИЛИ» и «НЕ-И», построенные на основе соотношения (6). 0-1- о о-п, Ьть-а-п -Ъп-Л-\ 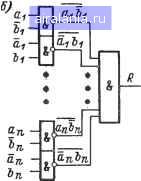 Рис. 15. Схемы, выявляющие совпадение двух кодов {R=\ при А=В) Схемы, выявляющие большее (или меньшее) из двух сравниваемых чисел (схемы ВБЧ), рассмотрим на примере сравнения двух двоичных чисел Л=0123..., с„ и В = Ьф2Ьз..-, Ьп, причем Oi и bl - старшие разряды, с„ и Ьп - младшие разряды. Схема ВБЧ должна обеспечить на выходе сигнал (обозначим его N), равный единице, в случае, если А>В. Если же АВ, то сигнал на выходе такой цепи должен быть равен нулю. Для получения логической функции, которую должна реализовать схема ВБЧ, можно, как и в случае схемы ВСК, взять за основу ячейку, сравнивающую одноразрядные коды. При этом, очевидно, а>Ь, если а= 1 и Ь = 0, т. е. аЬ= 1. Сравнение многоразрядных чисел можно проводить следующим образом. Вначале сравниваем коды в первом, старшем разряде. Если ai>bi {aibi = l), то можно сразу, независимо от содержания остальных разрядов, делать вывод, что А>В. Если Же в первом разряде коды совпадают (т. е. Cifei-1-Cifei= 1), то "следует, очевидно, проанализировать соотношение кодов во втором разряде Сг и 62. Если совпадают числа в первом и во втором разрядах, то нужно рассматривать третий разряд, и т. д. 0 1 2 3 4 5 6 7 8 9 [10] 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 0.0079 |