щим номеру выхода (см. цифры у выводов рис. 28,в), можно написать следующие равенства:

г/и = xXsX + ХхУъ = xXsXi (xi + г/9).

В соответствии с этими соотнощениями заполним таблицу функционирования триггера (табл. 9).

Как видно из таблицы, триггер сохраняет свое прежнее состояние (г/9=11; г/и = г/9) только в одном случае (строка 4),

когда Xi = 0, XzXsXi,= l, 7X8=1. При двух сочетаниях входных сигналов, соответствую- , .

щих строкам 1 и 5 таб- "

лицы, схема теряет триггер ные свойства: на обоих выходах (г/9 и г/ц) получим сигнал нуль. Если считать прямым и инверсным выходами триггера соответственно его №1воды 9 и И (Q=y9; Q=yu), то для установки триггера в нуль нужно подать входные сигналы, соответствующие строкам 2 или 6 табл. 9. Для установки в единицу на вход триггера должны быть поданы сигналы, указанные в строках 3, 7 или 8.

Исходя из сказанного, можно найти возможные варианты выполнения регистра памяти на триггерах К2ТР171. Выбе-. рем, например, для реализации регистра строки 4, 6 и 8 табл. 9. Строка 4 будет соответствовать хранению информации, строка 6 - записи единицы и строка 8 - записи нуля. Тогда для построения регистра можно подать на входы 2 и 1 триггера тактовые импульсы и их инверсию, на вход 3 - записываемую информацию /, на вход 4 - потенциал единицу, а на входы 7 и 8 - потенциал нуль (рис. 28, в). При этом потенциал С=0 будет удерживать входные сигналы такими, какими они указаны в строке 4 таблицы. При С=1 в зависимости от того, чему равен сигнал / - единице или нулю, получим входные сигналы, соответствующие строкам 6 или 8 таблицы. «

Для реализации регистра можно также выбрать строки 4, 3 и 2 табл. 8. В этом случае на входы 1 и 4 нужно подать постоянный потенциал единицу, на входы 2 и 7 - тактовые импульсы С, а на входы 3 и 8 - соответственно - прямой и инверсный сигналы записываемой информации (/-/).

Подобным образом, находя логические функции для выходных сигналов имеющегося в наличии триггера, всегда можно определить способы управления этим триггером.

Регистры памяти на триггерах, тактируемых фронтом, по принципу построения не отличаются от рассмотренных выще. При переходе единица - нуль (или нуль - единица) на такто-

I-I-

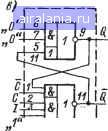Рис 28. Схемы включения триггеров в регистры памяти

вом входе С триггер устанавливается в состояние, определяемое потенциалами на управляющих входах.

Регистры памяти с записью прямого и инверсного значений кодов могут оказаться необходимыми, например, при построении цифровых приборов для измерения знакопеременных величин. В зависимости от сигнала на управляющей щине N (рис. 28, г) триггеры подобного регистра устанавливаются в состояния, соответствующие или прямому коду поданной информации (Q = I при Л = 1) или инверсному (обратному) коду этой информации (Q=/ при Л/=0). Естественно, что в любом случае запись информации производится только при наличии разрешающего импульса на входе С.

В ячейке регистра на рис. 28, г для инвертирования входных сигналов используется цепь логической равнозначности. Сигналы, подаваемые с этой цепи на входы J и К триггера, определяются формулами:

Таким образом, если Л=1, то /=/ и К=1\ если же N=0, т(Г/=Ги К=1.

Более сложная задача возникает тогда, когда нужно иметь возможность осуществлять запись в регистр памяти в прямом и обратном коде двоично-десятичного числа. Дело в том, что обратный код одноразрядного десятичного числа - это код, соответствующий числу, дополняющему данное до девяти. Если же мы будем просто поразрядно инвертировать двоично-десятичный код, то получим код числа, дополняющего данное до двоичного числа 2"--1, п - число двоичных разрядов. Поэтому на входе регистра памяти необходимо строить логические цепи, преобразующие обратный двоичный код в обратный двоично-десятичный код.

Рассмотрим эту задачу на примере щироко распространенного двоично-десятичного кода 8-4-2-1.

В табл. 10 приведены кодовые комбинации исходных двоично-десятичных чисел, обратных им двоичных чисел и обратных двоично-десятичных чисел. Из таблицы видно, что поразрядное

Таблица 10