Еще три двоично-десятичных счетчика показаны на рис. 37.

Счетчик по схеме рис. 37, а работает в коде 5-2-1-1 (табл. 17), называемом иногда в иностранной литературе кодом Уайта [42]. Сравнивая счетчики рис. 36, в и рис. 37, а, нетрудно увидеть, что они построены в общем-то одинаково. Только в счетчике рис. 36, в вначале включен делитель на 2, а затем делитель на 5, а в счетчике рис. 37, а - наЬборот: вначале делитель на 5, а затем на 2.

Счетчик по схеме рис. 37,6 работает в коде 5-4-2-1 (табл. 18) и построен также путем взаимной перестановки делителей на 2 и на 5, входящих в счетчик рис. 36, а.

Десятичный счетчик, схема которого показана на рис. 37, в [4], работает в невзвещенном коде, последовательно принимая состояния, указанные в табл. 19. Достоинством этого счетчика является то, что он содержит только четыре тактируемых /K-триггера - для его построения не требуется дополнительных логических ячеек. Очевидно, что на основе структуры рис. 37, в можно построить еще один вариант счетчика, если переставить местами делитель на 2 и делитель на 5.

Счетчики, работающие в самодополняющихся кодах, показаны на рис. 38.

Счетчик со структурой рис. 38, а работает в самодополняющемся коде 2-4-2-1 (табл. 20), в иностранной литературе называемом иногда кодом Айкена [42].

Таблица 17

Таблица 18

Таблица 19

: . в этом счетчике логическая цепь построена так, что после Г / кодовой комбинации 0100 счетчик совершает недвоичный пере-4 ход-устанавливается в состояние 1011. В результате кодовая . комбинация для числа, дополняющего любое данное число до 9, может быть получена поразрядным инвертированием кодовой комбинации данного числа.

Счетчик, структура которого показана на рис. 38,6, отли-" чается от счетчика рис. 38, с только тем, что в нем вход второй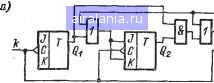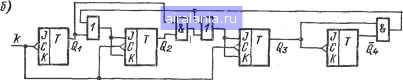

J 4с

Рис. 38. Двоично-десятичные счетчики, работающие в самодополняющнхся кодах: 2-4-2-1 (а); коде с избытком 3 (б) и 4-2-2-1 (в)

. ячейки «И» присоединен не к инверсному, а к прямому выходу четвертого триггера cq4). Если счетчик рис. 38, а не использует шести кодовых комбинаций в середине табл. 12, то для счетчика рис. 38, б неиспользуемыми являются три верхние и три нижние комбинации табл. 12. Десятичное число Л, записанное в счетчике рис. 38,6, может быть определено по формуле:

Л=8(Э4 + 4(2з + 2(22+С1-3.

Поэтому соответствующий этому счетчику двоично-десятичный код (табл. 21) носит название кода с избытком 3. ; Счетчик, показанный на рис. 38, в, работает в предложенном " автором самодополняющемся коде 4-2-2-1 [23]. Достоин-ством этого счетчика является простота реализации, что можно

Таблица 20

Таблица 21

Таблица 22

увидеть, сравнивая рис. 37, в с рис. 37, а и б. Логическая ячейка «ИЛИ», входящая в счетчик, в данном случае разрешает установку в нуль второго триггера входным импульсом k, если третий или четвертый триггеры находятся в нуле. В результате второй триггер совершает 3 недвоичных перехода и счетчик последовательно проходит кодовые комбинации (помещенные в табл. 22).

Десятичные счетчики на универсальных /Л"-триггерах. Описанные выше десятичные счетчики вьшолнены на тактируемых /К-триггер ах. Если же применить универсальные С-триггеры, то схемы счетчиков можно несколько упростить, используя нетактируемый режим работы отдельных триггеров. Так, на рис. 39 показаны схемы счетчиков на универсальных С-триггерах, работающих соответственно в коде 8-4-2-1 и в коде 4-2-2-1 (табл. 16). В отличие от аналогичных счетчиков на тактируемых JK-триггерах (рис. 36, айв) они не содержат дополнительных логических ячеек.

Десятичные счетчики на DT- п SR-триггерах. В некоторых сериях логических