На рис. 45, а показана схема двоично-десятичного синхронного реверсивного счетчика, работающего в коде 8-4-2-1. Кроме двоичных реверсивных межтриггерных связей, в счетчике рис. 45, а существуют дополнительные цепи, обеспечивающие недвоичный переход от кода 1001 к коду 0000 при суммировании и обратный переход при вычитании.

Найдем выражения для сигналов на управляющих входах триггеров, входящих в счетчик рис. 45, а. Вначале запишем логические функции для тех входов, на которых сигналы такие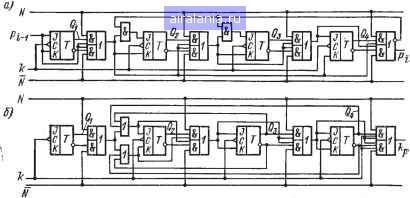

Рис. 45. Реверсивные двоично-десятичные синхронные счетчики, работающие в коде 8-4-2-1 (а) и самодополняющемся коде 4-2-2-1 (б)

же, как и в двоичном реверсивном счетчике (индексы у обозначений входов соответствуют номерам триггеров):

K3 = Pi-i{QiQ2N + QiQ2 N)

J, = Pix (QQsQN + Qa Qs Q4 ) В этих равенствах Pj-i - это потенциальный сигнал переноса с предыдущего десятичного разряда. Найдем выражение для сигнала переноса Pi на выходе данного разряда:

Сигналы, отличные от сигналов двоичного счетчика, возникают на входах /г, /з и Kt- Найдем их:

= PiPi-i {QiN + QiN) = Pc-i {QNQ, + QiNQQsQ,);

Js = PcPi-i {QiQN + QiN) = Pi-x {QiQNQ, + QiQNQsQ,); .

K, = K2 = P, , (QiN + QiN)-Полученные формулы показывают, что второй триггер при сложении {N=1) устанавливается в единицу (/2=!) только при условии, что четвертый триггер находится в нуле, а при вычита-

НИИ (N=0) -только при условии, что второй, третий и четвертый триггеры не находятся одновременно в нуле. Третий триггер также может при сложении опрокинуться в единицу только при условии, что четвертый триггер находится в нуле, а при вычитании- при условии, что третий и четвертый триггеры не находятся одновременно в нуле. Установка в нуль четвертого триггера может происходить каждый раз тогда, когда есть разрешающий сигнал на входе К второго триггера.

Все эти условия нужны как раз для того, чтобы обеспечить в счетчике рис. 45, а недвоичный переход 1001-0000 при сложении и переход 0000-1001 при вычитании.

Рассмотрим теперь процесс синтеза двоично-десятичных реверсивных счетчиков на примере синтеза счетчика, работающего в предложенном автором самодополняющемся коде 4-2-2-1 (табл. 22). Из табл. 22 видно, что как при суммировании, так и при вычитании недвоичные переходы происходят только во втором триггере. Поэтому в данном случае достаточно найти структуру логических цепей, обеспечивающих получение нужных сигналов на входах J и К второго триггера, а на входах остальных триггеров логические цепи будут такими же, как и в двоичном счетчике.

Составляем табл-. 25 с указанием потенциалов Jz и Kz, необходимых для того, чтобы обеспечить требуемую последовательность кодовых групп при сложении и при вычитании. Прочерки в таблице, как было принято раньше, означают, что потенциал на входе может быть любым, О или 1.

Как при сложении, так и при вычитании поведение триггера определяется тем, какие потенциалы присутствуют на его управляющих входах к моменту прихода разрешающего фронта на тактовый вход. Поэтому, заполняя табл. 25, против данной кодовой комбинации нужно записывать такие входные потенциалы Jz и Kz, которые обеспечат переход к последующей кодовой группе (нижней - при сложении и верхней - при вычитании).

Выпишем теперь из табл. 25 потенциалы /г и /Са в клетки диаграмм Вейча (табл. 26). Разные цифры в клетках, разделенных пополам по диагонали в диаграммах табл. 26, говорят о том, что для данного набора аргументов функция должна принимать разные значения в зависимости от того, какой режим установлен в счетчике, суммирование (верхние цифры) или вычитание (нижние цифры). Незаполненные клетки диаграмм указывают кодовые группы, которые не используются в данном двоично-десятичном коде.

Теперь, исходя из диаграмм табл. 26, составим логические функции так, чтобы при суммировании (Л=1) и при вычитании (Л=1) получить требуемые значения сигналов /г и Kz-

Таблица 25

Таблица 26