мер из-за возможных катастрофических последствий или угрозы здоровью людей.

Недостаток рассмотренного метода заключается в том, что пределы допускаемой погрешности являются обобщенной оценкой, в которой нельзя выделить систематическую и случайную составляющие погрешности.

3.3. РАСЧЕТ ПОГРЕШНОСТИ ИЗМЕРЕНИЙ С УЧЕТОМ МЕТОДИЧЕСКОЙ ПОГРЕШНОСТИ

По известной инструментальной погрешности можно рассчитать погрешность измерений, если учесть методическую и субъективную погрешности. Субъективная погрешность при достаточно высокой квалификации оператора пренебрежимо мала, и в дальнейшем она учитываться не будет. Таким образом, общая погрешность измерений А = А„--Л„, где А„ и А„ - инструментальная и методическая погрешности.

Поскольку рассмотренный метод нормирования инструментальной погрешности - это метод наихудшего случая, то и при оценке погрешности измерений следует так выбирать верхнюю Ав и нижнюю Ан границы погрешности А, чтобы в пределы от Ав до А„ попали все погрешности при наименее благоприятном сочетании отдельных составляющих. Рассмотрим частные случаи вычисления погрешности.

Методическая погрешность постоянна, и ее значение известно: А„ = Э„. В этом случае она имеет систематический характер, и следует ввести поправку в показание. Исправленный результат измерений х„с = х -6„. Границы интервала х--А„г, и х -А„п также сместятся на -9„ (рис. 3.3, а), а протяженность интервала не изменится. Результат измерений записывают в виде

л:„с±А„, P = \, (3.3)

где Ап = А„п - предельная погрешность измерений.

Поскольку при задании погрешностей их пределами всегда выполняется условие P -\, то для более компактной записи результат обычно приводят без указания вероятности: x„c±An. Такой формы записи мы будем придерживаться в дальнейшем.

д;-Л,. у у,. А Х-Лйп X Х+Ли,п

f................J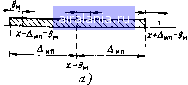

Х-0.5(Л„д*й„)

I

Результат можно представить как х\ Д„п -в„; -Д„п -0м; с несимметричными относительно х границами. Такая форма менее удобна, и в дальнейшем мы ее использовать не будем.

Пример 3.2. Определим результат измерений напряжения для источника • питания с выходным сопротивлением 10 кОм для условий, перечисленных в примере 3.1. Как показано в примере 2.1, методическая погрешность 6„ = = -/?/(Рвх + Р;)= - 10" откуда 6„ = (Уб» =-0,0064 В. Результат измерений согласно (3.3) примет вид: 6,388 + 0,015 В.

Методическая погрешность задана верхним и нижним пределами: Д„в и Д„„.

Как это следует из рис. 3.3, б, наихудший случай соответствует границам интервала х -Д„п -Д„в и х--Д„п -Дмн. Протяженность интервала увеличится и составит х--Д„п -Дмн -> + Дип--Дмв = = 2Дип -Дмн--Дмв. Для того чтобы записать результат с симметричными пределами погрешности, следует ввести поправку - 0,5(Д„в + Д„н), а погрешность увеличить на 0,5(Д„в -Дмн). Результат измерений

х„с±Дп, (3.4)

где х„с = х -0,5(Д„в + Дмн), Дп = Дип + 0,5(Д„в -Дмн).

Пример 3.3. Определим результат измерений для условий примера 3.2, если известно, что выходное сопротивление источника питания лежит в пределах 0...10 кОм. Расчет по формуле, приведенной в примере 2.1, дает А„„ = 0; А„в = = -0,0064 В. Согласно (3.4) результат измерений 6,385 + 0,018 В.

3.4. НОРМИРОВАНИЕ ПОГРЕШНОСТЕЙ СРЕДСТВ ИЗМЕРЕНИЙ СТАТИСТИЧЕСКИМИ МЕТОДАМИ

Этот метод основан на учете статистических свойств погрешностей и позволяет отдельно учитывать систематические и случайные составляющие.

Оценка инструментальной погрешности. Если экспериментатор выбрал средство измерений случайным образом, то ему неизвестно конкретное значение систематической погрешности, и эту погрешность можно рассматривать как случайную величину. Ее конкретное значение остается неизвестным, но она подчиняется закону распределения, который можно определить для совокупности средств измерений данного типа. Систематическую погрешность характеризуют числовыми значениями, например математическим ожиданием 9 и средним квадратическим отклонением 09.

в нормальных условиях общая инструментальная погрешность средств измерений данного типа Аи = 9 + е. Определив математическое ожидание от правой и левой частей равенства, получим: Аи = 6, поскольку 8 = 0. Это значит, что среднее значение погрешностей, полученных при измерениях с многократными наблюдениями с помощью разных экземпляров средств измерений данного типа, приближается к 6.

Среднее квадратическое отклонение погрешности А„

2 2,2

Ои = Ое + Ое

зависит не только от среднего квадратического отклонения случайной погрешности, но и от рассеяния систематических погрешностей разных экземпляров средств измерений.

Заметим, что случайные величины е и 9 имеют разный характер. Погрешность е проявляется в виде случайной величины при измерениях с многократными наблюдениями, выполненных определенным экземпляром средств измерений. Случайный характер погрешности 9 проявляется при рассмотрении всей совокупности средств измерений данного типа, ее характеристики нельзя определить по одному экземпляру средств измерений.

Случайную погрешность средств измерений делят на три составляющие: собственную погрешность 8соб, погрешность в„, обусловленную гистерезисом, и погрешность квантования е,, зависящую от цены деления [i младшего разряда показания средств измерений:

8 = 8соб ~Н "Ь 81.

Собственная погрешность характеризует рассеяние результатов многократных наблюдений при отсутствии вариации показаний или тогда, когда влияние гистерезиса исключено. Как показано в § 2.4, погрешность, обусловленную вариацией показаний, считают распределенной по равномерному закону СКО о„ = = Н/л/12. Третья составляющая характеризует погрешность дискретизации, ее СКО а = ц/-\[]2.

Полагая составляющие случайной погрешности независимыми, получаем

o.=[aL + (l/I2)(w + (i)],

о„ =(ов + 0?) =[0Но?об + (1/12) (и + i

Значения Особ и Н для разных экземпляров средств измерений данного типа несколько различаются, и для расчета общей инструментальной погрешности берут их предельные значения Особ п и Н„, которые приводят в паспортных данных.