

|
|
Главная -> Понятия метрологии 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 [17] 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 сверху для измерений погрешностей измерений любым экземпляром средств измерения данного типа. Следуя этой методике, погрешность косвенных измерений можно оценить предельным значением, полученным для наименее благоприятного случая. Предельная погрешность А„ = 2 <5/ (3.23) дает сильно завышенную оценку. Результат измерений Унс±Ап. Существует и другой способ суммирования погрешностей Д, аргументов, основанный на математическом моделировании свойств погрешностей. Погрешности Д, считают случайными, статистически независимыми и подчиненными равномерным законам с границами ±Дга. Для таких погрешностей СКО An,/V3 Согласно (3.18) СКО результата косвенных измерений Если число аргументов велико, то в силу центральной предельной теоремы погрешность изменений у можно считать распределенной по гауссовскому закону. Тогда границы погрешности при Рд = 0,95 -.1/2 г- п -. 1/2 Дв„= 1,96 2()aL/3 Границы погрешности рассчитывают по формуле -, 1/2 2(1-) Д.„ = Результат измерений У„с ± Двн (3.24) записывают без указания вероятности. Вероятность Яд = 1 в этом случае не обеспечивается. Пример 3.10. Определим результат косвенных измерений резонансной частоты контура fp==0,5(fi + /2), где fi и /2 - частоты, соответствующие границам полосы пропускания и измеренные непосредственно частотомером. Результаты прямых измерений: fi = 163,83 кГц; Д„,=0,03 кГц; 9», = -0,04 кГц; /2=169,33 кГц; Д„2 = = 0,05 кГц; 6м2=-0,06 кГц. За оценки значений частот примем исправленные результаты прямых измерений /,-е», = 163,87 кГц; /2 -9„2= 169,39 кГц. Резонансная частота fp = 0,5(/i-0„,+/2 -е„2)= 166,63 кГц. Получим расчетные формулы для оценки погрешностей Согласно (3.24). Производные a/p/a/i=(9fp/a/2 = 0,5, поэтому Abh = 0,5(Ai+A2) =0,029 «0,03 кГц. Результат косвенных измерений 166,63±0,03 кГц. Оценка погрешности по (3.23) дает несколько больший результат: An = 0,5(A„i + + А„2) = 0,04 кГц. Погрешности, рассчитанные по формулам (3.23) и (3.24), различаются тем меньше, чем сильнее отличаются слагаемые {df/dxi)A„i и чем меньше их число. Наибольшее различие полученных по (3.23) и (3.24) погрешностей будет при одинаковых слагаемых, оно возрастает с ростом числа слагаемых. Например, если все слагаемые равны единице, то при двух слагаемых Дп = 2 отличается от Двн=1,4 всего на 30%, а при десяти слагаемых Дп=10, Двн = 3,2, т. е. погрешности отличаются в три раза. Погрешности, нормированные статистическими методами. В этом случае методические погрешности измерений параметров Xi необходимо задать в виде систематических составляющих 0„, и СКО Ом, случайных составляющих. Затем эти погрешности суммируют с соответствующими составляющими инструментальных погрешностей. Систематические погрешности измерений параметров в + Эм, вычитают из результатов и получают исправленные результаты Xbc< = x, -9, -9„„ затем вычисляют результат измерений y„c = /(x„ci, Хкс2, Хтп). Срсднис квадратическис отклонения методических о», инструментальных 0„, погрешностей суммируют подобно тому, как это делали при оценке погрешностей прямых измерений. Результат измерений г/„с ± t , Рд. (3.25) 3.7. ПОГРЕШНОСТИ ПРИ ОПРЕДЕЛЕНИИ ПОЛОЖЕНИЙ ЭКСТРЕМАЛЬНЫХ УРОВНЕЙ И ЗАДАННЫХ УРОВНЕЙ Для описания характеристик некоторых цепей, например АЧХ узкополосных устройств, иногда достаточно двух параметров: полосы пропускания, определенной на заданном уровне, и значения частоты, соответствующего максимуму частотной характеристики. Погрешности измерения подобных параметров имеют определенные особенности. Погрешность при определении положения экстремального уровня. Положение экстремального уровня определяют с помощью индикаторов экстремальных уровней, позволяющих судить о достижении экстремальных значений подводимой к индикатору вели- чины. Например, настройку колебательного контура в резонанс можно контролировать с помощью вольтметра, измеряющего амплитуду напряжения на конденсаторе. Резонансное значение частоты отсчитывают по шкале генератора, питающего контур. Пусть зависимость показаний индикатора a = f{x) от измеряемой величины X имеет вид, показанный на рис. 3.5. При измерениях оператор плавно изменяет величину х, одновременно наблюдая показания индикатора, пока не будет достигнут экстремальный уровень аэ, и отсчитывает значение Хэ. Погрешность Да индикации экстремума, зависящая от свойств индикатора, связана с погрешностью Д соотношением: - + 2 dx где производные взяты при х = Хз. Поскольку в этой точке df/dx = 0, то Предельная погрешность Дп определения х будет соответствовать такому отклонению Да , которое может быть обнаружено оператором. Это отклонение оценивают разрешающей способностью Дар экстремального индикатора. Тогда предельная погрешность Ап = 2Дар/ (3.26) Для индикаторов со стрелочными указателями разрешающую способность принимают равной 0,2...0,5 деления шкалы, а для цифровых приборов она составляет единицу младшего разряда показаний. Заметим, что систематическая погрешность приборов, используемых в качестве экстремальных индикаторов, несущественна, поскольку в процессе измерений необходимо лишь зафиксировать наличие экстремума. Погрешность при измерении положения заданного уровня. Пусть необходимо определить положение Хур заданного уровня аур = /(ат, определенного по известной характеристике rx = f{x)  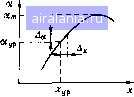 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 [17] 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 0.0074 |