

|
|
Главная -> Понятия метрологии 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 [25] 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 деленных по гауссовскому закону, эффективной оценкой является среднеарифметическое, поэтому отношение Ос/о„< \ при любых п. Пример 4.5. Определим число измерений, необходимое для получений СКО оценки математического ожидания 0,1 мВ, если погрешность распределена по равномерному закону с СКО а=1 мВ. В данном случае оценка максимального правдоподобия - полусумма крайних членов вариационного ряда. Ее СКО рассчитывается по формуле, приведенной в третьем столбце табл. 4.8. Подставив в формулу значения СКО и решив полученное уравнение, получим п = 23. Если же математическое ожидание оценивать по среднеарифметическому, то СКО ас = а/п, откуда гг=100. Таким образом, при заданной СКО оценки максимального правдоподобия требуемое число измерений возрастает более чем в 4 раза. 4.5. ОБРАБОТКА РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ С МНОГОКРАТНЫМИ НАБЛЮДЕНИЯМИ, ПОДЧИНЕННЫХ ГАУССОВСКОМУ ЗАКОНУ Полученные в § 4.4 оценки максимального правдоподобия х и S называют точечными оценками результата измерений. В некоторых случаях удобнее пользоваться интервальной оценкой - интервалом, в котором с заданной вероятностью лежит измеряемая величина. Пусть результаты наблюдений подчинены гауссовскому закону, статистически независимы и не содержат систематических погрешностей. Оценка математического ожидания и дисперсии. Оценка максимального правдоподобия (4.4) несмешенная, поскольку Определение ее таким образом можно рассматривать как косвенные измерения, поэтому СКО оценки 4=1па = -. (4.9) Оценка х подчиняется гауссовскому закону распределения при любых п, поскольку композиция гауссовских законов при любом числе слагаемых дает гауссовский закон. Плотности вероятности p{xi) и р{х) показаны на рис. 4.8. Использовать закон распределения р{х) для отыскания доверительного интервала нельзя, так как значение а, а следовательно, и oj обычно неизвестны. Вместо а при анализе используют Оценку максимального правдоподобия ее (4.5). Определим, является ли эта оценка несмещенной. Для этого найдем математическое ожидание и после преобразований получим = \{п-\)/п]о\  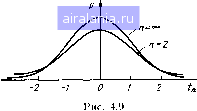 Следовательно, оценка максимального правдоподобия о при конечном п является смещенной. При л-+оо [(п-1)/п]-оо и а->-а, откуда следует асимптотическая несмещенность оценки. При расчетах используют несмещенную оценку п - 1 п - 1 (4.10) Подставив полученную оценку в (4.9), получим оценку СКО среднеарифметического -г--гг 2 ( х,- - х) -, /2 (4.П) которая является случайной величиной. Доверительная вероятность. Вероятность пребывания оценки на интервале от X - tnSi до X-\-tnSi, выраженная в долях оценки СКО, Р{Х - tnSi < X < X + tnSi } = Р!х - tnSi < Л" < X + tnSi определяет и вероятность пребывания истинного значения X на интервале от х - tnSi до x-\-tnSi. Этот интервал случаен, так как его центр и протяженность - случайные величины. Такой интервал, как и вероятность Рд, называют доверительным. Заметим, что термин доверительная вероятность, введенный в математической статистике, применим только в случае задания интервала со случайными границами. Для обозначения доверительной вероятности и модуля доверительных границ интервала для возможных погрешностей будем, как и ранее, пользоваться символами Рд и Лвн. Для определения доверительной вероятности следует определить плотность вероятности случайной величины е = (х -A)/sj, а затем проинтегрировать ее от - tn до („. В теории вероятности показано, что случайная величина е распределена по закону Стьюдента с плотностью вероятности р„(е), зависящей от числа измерений п: р (г) - r(»/2) / , " п{п-\)Г\{п-\)/2]\ п-0 -п/2 где Г - гамма-функция. Зависимости плотности вероятности Рп{г} для п = 2 и п=оо показаны на рис. 4.9. При «-оо распределение Стьюдента стремится к гауссовскому. Как следует из рис. 4.9, основное отличие распределения Стьюдента от гауссовского заключается в более медленном убывании плотности вероятностей с ростом е. Доверительная вероятность Эта функция табулирована. Некоторые значения /„, соответствующие доверительной вероятности Рд((, „) = 0,9, 0,95 и 0,99, приведены в табл. 4.8. Таблица 4.8. Значения t„ при заданной вероятности Яд{/, п)
Пример 4.6. Пусть при пяти результатах наблюдений, подчиненных гауссовскому закону, получены оценки л= 10,00; s = 0,2. Для доверительной вероятности Я(/, /!) = 0,95 Двн = n.s/V" = 0,25 доверительный интервал 10,00 + 0,25. В случае точного задания СКО о = 0,2 Д,„ = го/-\/п =0,18 и доверительный интервал станет значительно меньше: 10,00±0,18. Еще больше различаются интервалы для больших значений доверительной вероятности, например P{t, п) = 0,99. Это обстоятельство обусловлено более медленным убыванием с увеличением t„ плотности вероятности распределения Стьюдента по сравнению с гауссовским законом. 4.6. НЕИСКЛЮЧЕННЫЕ СИСТЕМАТИЧЕСКИЕ ПОГРЕШНОСТИ И ИХ УЧЕТ Возникающие при измерениях систематические погрешности обычно учитывают внесением поправки в результат измерений и оценкой измеряемой величины исправленным результатом. Систематические погрешности, а следовательно, и поправки всегда из- 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 [25] 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 0.0128 | ||||||||||||||||||||||||||||||||||||||||