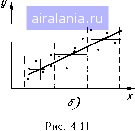сверху и снизу (рис. 4.11, а). График искомой математической модели строят как центральную линию полученного контура.

При больших погрешностях и часто встречаюшихся промахах из-за возрастания неопределенности при построении контура и центральной линии метод контура становится мало эффективным. В таких случаях можно использовать метод медианных центров, основанный на устойчивых к промахам медианных оценках среднего значения. Все поле экспериментальных точек делят на несколько областей. Например, на рис. 4.11,6 выделены три области, ограниченные штриховыми линиями. В каждой области находят медианный центр. Для этого проводят горизонтальную линию, выше и ниже которой число точек одинаково (по две точки в каждой области), а затем вертикальную линию, справа и слева от которой число точек также одинаково. Медианные центры, лежащие на пересечении линий, соединяют плавной линией.

Медианные оценки можно использовать для исключения промахов. Например, при монотонно изменяющихся отсчетах вместо очередного отсчета берут медиану трех соседних отсчетов. Так, на рис. 4.11, в исходные результаты показаны точками, причем точка 4 выпадает из общей зависимости. Если ни один из трех соседних отсчетов не содержит промаха, то медианные значения (на рис. 4.11, в отмечены знаком -f) совпадают со средними отсчетами. Например, медианное значение для точек /, 2, 3 совпадает с точкой 2. Среди точек 2, 3, 4 точка 4 содержит промах, но медианное значение совпадает с исходной точкой 3. Медианное значение точек 3, 4, 5 соответствует точке 5, так что вместо точки 4 при дальнейшей обработке используют точку 5, не содержащую промаха. При двух следующих подряд промахах метод неэффективен.

Выбор математической модели. Вид зависимости y = f{x), описывающей опытные данные, выбирает экспериментатор на основе предварительных данных о природе исследуемой зависимости или о расположении экспериментальных точек. Крайне желательно, чтобы модель была содержательной, т. е. чтобы входящим в нее постоянным можно было приписать определенный физический смысл. Пусть, например, измерены текущие значения темпе-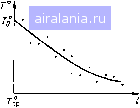

Рис. 4.12

Рис. 4.13

ратуры Т° тела, сначала нагретого до 7"о и охлаждающегося до температуры Т°р окружающей среды (рис. 4.12). В математической модели вида Т° = {То-7"?р)ехр( - t/т) постоянную времени т можно рассматривать как тепловую постоянную времени тела, зависящую от его объема и удельной теплоемкости. Если же указанную экспериментальную зависимость представить в виде полинома, то его коэффициенты никакого физического смысла иметь не будут.

Математическая модель должна описывать результаты эксперимента наиболее компактно, что в дальнейшем упрощает ее использование. Однако стремление к простоте модели может противоречить ее адекватности исследуемой зависимости. Разумную степень усложнения модели в зависимости от целей эксперимента определяет экспериментатор. Например, для показанной на рис. 4.13 совокупности экспериментальных точек линейная модель / характеризуется большой погрешностью адекватности, так как при крайних значениях аргумента линия выходит за пределы поля рассеяния точек. Модель 2 в виде полинома второй степени также дает значительное расхождение при максимальных значениях х. Более подходящей оказывается математическая модель 3 в виде полинома третьей степени.

При использовании аналитических способов расчета задача выбора математической модели решается в два этапа. Сначала находят общий вид математической модели, а затем рассчитывают параметры, определяющие ее конкретный вид. Если нельзя указать общий вид модели теоретически, то ее определяют по форме поля рассеяния экспериментальных точек. Для этого в поле рассеяния помещают графики различных известных функций и находят такие, которые отражают особенности этого поля. Такой выбор неоднозначен, так как обычно можно найти несколько подходящих функций.

В некоторых частных случаях подбор математической модели упрощается, если масштабы по осям х и у выбрать так, что график аппроксимирующей функции превратится в прямую линию. Например, степенная функция у = ах" (рис. 4.14, а) после логарифмирования приобретает вид lg(/= Iga + ftlgx, и ее графическое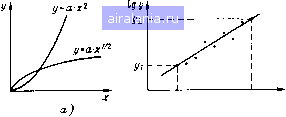

1 \лх

Рис. 4.14

изображение в координатах Igx, Igy является прямой линией с угловым коэффициентом п. Для проверки модели в этих координатах строят экспериментальные точки (рис. 4.14, б). Если точки располагаются возле прямой линии, то математическую модель в виде степенной функции считают не противоречащей экспериментальным данным. По графику можно грубо оценить параметры модели. Для этого проводят линию, берут на ней две точки с координатами Xl, уь Х2, 1/2 и рассчитывают угловой коэффициент и параметр а:

(4.15)

График показательной функции у = ае" превращается в прямую линию, если выбрать полулогарифмический масштаб с координатой Igy по оси у. Построив в такой системе координат экспериментальные точки, можно оценить приемлемость модели в виде показательной функции и приближенно оценить параметры а к Ь. Гиперболические функции строят в системе координат х, \/у.

Применяя функциональные шкалы, можно использовать рассмотренный метод и для некоторых других моделей.

Метод наименьших квадратов. После того как установлен вид математической модели, аналитическими методами рассчитывают ее параметры. Наиболее распространен метод наименьших квадратов. Сущность метода состоит в таком выборе параметров мо-

мини-

дели, при которых сумма квадратов отклонений 2 (у - У() мальна. =i

Если систематическая погрешность измерений значений у,-отсутствует, случайная погрешность подчинена гауссовскому закону с постоянной дисперсией, а погрешности последовательных измерений статистически независимы, то вычисленные с помощью метода наименьших квадратов значения параметров математической модели являются оценками максимального правдоподобия. На практике эти условия выполняются редко, и метод наименьших квадратов является просто удобным аналитическим способом расчета параметров математической модели.