Рассмотрим применение этого метода на примере простейшей линейной модели у = ао-{-utx. Сумма квадратов отклонений результатов экспериментальных данных от модели

{У1 - У) = Z{yi - ao - aiX,) . i= 1 ;= i

Сумма минимальна, если

д1{у1-уУ /дао = Ои д1.{у-уУ /да, = 0. После дифференцирования получим систему уравнений

ао« -f fli 2 X, = 2 (/,,

п п п

Оо 2 Х; -f а, 2 xf = 2 Xi yi,

i= 1 i= i i= i

(4.16)

называемую системой нормальных уравнений. Нормальные уравнения линейны относительно неизвестных коэффициентов ао и ai, и систему можно решить методами линейной алгебры. Полученные значения коэффициентов определяют положение прямой, называемой линией регрессии. Коэффициенты ао и а\ называют коэффициентами регрессии.

Расчет коэффициентов регрессии можно упростить, если преобразовать нормальные уравнения и подвергнуть предварительной обработке экспериментальные данные. Для этого, поделив первое уравнение (4.16) на п, получим ao-f-aiX = y, где

X = Xj-, 1/ = -2 (/i - среднеарифметические значения

i= I i= 1

X w у. Если перенести начало координат в точку х = х, то в новой системе координат первое уравнение будет иметь вид

1 - п

Оо -f- fli 2 ---= У- Поскольку 2 Xi - X = О, то

= = 2(/i , (4.17)

Следовательно, коэффициент оо равен среднеарифметическому значению у.

Рис. 4.15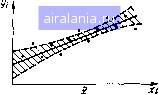

В новой системе координат второе уравнение ао2(х, -х) -f

п п п

+ щ liixi - х) = 2 (X, - х) У; преобразуется к виду а, 2 (х,- -

- х) == 2 (х, - х)у„ откуда а, = 2 {xi - х)у, /2 (л:,- - х). (4.18)

Таким образом, предварительное центрирование результатов экспериментов позволит существенно упростить решение системы нормальных уравнений. Линия регрессии, а также экспериментальные точки показаны на рис. 4.15.

Погрешность модели. Из-за рассеяния экспериментальных точек вследствие погрешностей измерений значения коэффициентов регрессии также определяются с погрешностью. Пусть рассеяние экспериментальных точек обусловлено единственной причиной - погрешностью измерений у„ причем среднее квадратическое отклонение о погрешности не зависит от х, а результаты измерений независимы. Тогда согласно (4.9) и (4.18) alo = a/n; Ста1 =

= o/2(xi -х) Погрешность оценок у по линии регрессии =

= огао+(х -x)aai состоит ИЗ двух составляющих: аддитивной и мультипликативной.

Погрешность оценки минимальна при х = х и возрастает с увеличением отклонения х-х. Область рассеяния для оценки показана на рис. 4.16 заштрихованной областью ограниченной пунктирными линиями. Она оказывается сушественно меньше поля рассеяния экспериментальных точек.

Особенности расчетов методом наименьших квадратов. С ростом числа экспериментальных точек и усложнением модели резко возрастает сложность расчетов параметров модели. Обычно их выполняют на ЭВМ, математическое обес-

печение которых содержит необходимые программы. В качестве математической модели часто используют полином, степень которого определяют, исходя из разумного усложнения модели.

Иногда приходится степень полинома выбирать в ходе расчетов. Сначала для полинома первой степени рассчитывают пара.метры и вычисляют сумму квадратов

отклонений -Г*! линейной модели от экспериментальных точек. При

недостаточно большой степени полинома, когда полученная прямая линия существенно выходит за пределы поля рассеяния экспериментальных точек, сумма в значительной мере определяется погрешностью адекватности модели.

Затем усложняют математическую модель, выбрав полином второй степени, и для него рассчитывают коэффициенты и определяют сумму квадратов отклонений. За счет уменьшения погрешности адекватности сумма оказывается меньше, чем для линейной модели. Процесс увеличения степени полинома продолжают до тех пор, пока сумма не перестанет значительно уменьшаться. Это свидетельствует о том, что погрешность адекватности стала малой по сравнению с погрешностью за счет рассеяния экспериментальных точек, и дальнейшее усложнение модели не имеет смысла.

Поскольку метод наименьших квадратов основан на минимизации суммы квадратов отклонений i/i - у. то на результат расчета параметров модели сильно влияют большие погрешности экспериментальных данных, которые могут быть вызваны промахами. Особенно сильно влияют погрешности экспериментальных точек, наиболее удаленных от центра поля рассеяния. Например, на коэффициент ai для линейной модели, а следовательно, и на его погрешность мало влияют зна-

чения у,, близкие к центру поля рассеяния, так как в сумме 2j - они

учитывают с малыми весовыми коэффициентами л, - х. С увеличением отклонений х, - х возрастает и вклад экспериментальных значений у,. Наибольшее влияние оказывают максимальное и минимальное значения.

Следовательно, промахи следует исключать при окончательной обработке экспериментальных данных. Существуют различные методы исключения влияния промахов. Так, экспериментальные данные можно цензурировать в ходе проведения эксперимента до обработки методом наименьших квадратов. Методы цензурирования, рассмотренные в §4.3, непосредственно применить невозможно, поскольку границы цензурирования должны автоматически отслеживать закономерные изменения. Эти изменения можно учесть методом экстраполяции. Например, при использовании интерполяционного полинома Лагранжа первой степени по двум точкам, предшествующим контролируемой, определяют коэффициенты полинома. Затем находят значение полинома в контролируемой точке. Относительно этого значения вычисляют верхнюю и нижнюю границы цензурирования. Если экспоненциальная точка лежит внутри границ, то ее оставляют. Если же экспериментальная точка окажется вне границ, то ее исключают и вместо нее вводят какое-либо подходящее значение, например предыдупую точку.

Так. для изображенных на рис. 4.16 экспериментальных данных по точкам 1 и 2 строят прямую линию и определяют экстраполируемое значение для точки 3.