тов, например ao{t), показан на рис. 5.2. В большинстве случаев эту зависимость можно приближенно представить как сумму флуктуационного гауссовского случайного процесса ео(/) и медленно меняющегося математического ожидания ao(t), показанного плавной линией. Следовательно, коэффициенты ao(t) = ao{t)-\-eo{t); ai(/) = ai(0 + ei(0- Будем далее считать, что за время измерений Т математические ожидания существенно не меняются. Случайные отклонения коэффициентов, полученные в результате наблюдений, разделенных интервалом времени Т», статистически независимы. Реальная градуировочная характеристика

y = aoit) + ai{t)x (5.5)

y={t) + a,{t)x + Eo{t) + et(t) X.

Сущность метода образцовых мер. Метод основан на последовательных измерениях измеряемой величины и однородных с ней образцовых величин (рис. 5.3, а). Поскольку в большинстве радиотехнических приборов измеряют параметры сигналов, то этот метод иногда называют методом образцовых сигналов. Сначала с помощью коммутатора к средству измерений подключают измеряемую величину X и в памяти вычислительного устройства фиксируют показание уо. Затем по команде с вычислительного устройства с помощью коммутатора последовательно подключают образцовые сигналы L\ и Li, ближайшие к х, и фиксируют показания у\ и у2 (рис. 5.3, б).

Предположим, что флуктуационные составляющие коэффициентов ао и а\ отсутствуют. Тогда полученные результаты отвечают системе уравнений

уо= ao(i) X,

yi = ао(/2) +ai(/2) и, yi = ао(.з) + a{t L2,

Средство измерений

Вычислительное устройство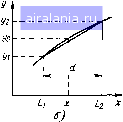

где tl, ti п ti - моменты, в которые производились измерения х, Li и L2. Если можно пренебречь изменениями математических ожиданий ао и ai на интервале времени з -Л, то их можно исключить из системы уравнений. Измеряемую величину вычисляют из соотношения

x=Li+f{yo-yi). (5.6)

Уг У\

Анализ погрешностей. Полученный результат свободен от систематической погрешности только в том случае, если погрешности образцовых сигналов пренебрежимо малы. Если же меры L\ и L2 характеризуются систематическими погрешностями 6 и 62, то согласно (3.11) систематическая погрешность определения

e,=[0i(L2-x)+e2(x-L,)]/(L2-Li).

Если известны предельные значения в„п1 и 6нп2 неисключенных систематических погрешностей образцовых сигналов, то СКО измерений

L{L2-x) +eL2(x-L,) ]/3(L2-L,) .

Рассмотрим теперь влияние на результат случайных состав-ляюших ео и 8.. Для этого из (5.6) определим прирашения измеряемой величины в зависимости от прирашений показаний

А. = 2 - LI )А,о + (х - L2)Ay I + (X - LI )Ау2]/а i(L2-Li). (5.7)

Прирашения показаний средства измерений

Ayo = eo(i) + ei(ii)x,

A„ = eo(M + e,(2)Li, (5.8)

Ау2=Ео(/з) +61(3)-2,

Подставляя (5.8) в (5.7), для статистически независимых составляюших ео и ei после преобразования имеем:

о1={К\о1о + lUxalja, (5.9)

й = +(/+(Ш

<1-+()()+(У(/.

Сопоставим полученное значение дисперсии случайной погрешности с дисперсией, которая характеризовалась бы при однократном измерении данным средством. Как это следует из (5.5), измеренное значение х связано с показанием г/о соотношением х =

= [y - ao(t)]/ai(t). Отсюда согласно (3.14) найдем дисперсию случайной погрешности измерения: ai = {aao-\-xal[)/ai{t).

Сравнивая это соотношение с (5.9), легко убедиться, что переход от метода с однократными наблюдениями к методу образцовых мер приводит к увеличению случайной погрешности, поскольку Ki> 1 и К1> 1.

Расчеты показывают, что максимальные значения K.i = К2 = 2 получаются, если x = Li или x = L2, и несколько уменьшаются по мере приближения х к середине интервала от Li до L2. В наихудшем случае

ol=2{alo + xoi;) /ai{t). (5.10)

Следовательно, при переходе от измерений с однократными наблюдениями к измерению методом образцовых сигналов дисперсия случайной погрешности возрастает в 2 раза, а СКО - в V2 раз.

Тестовый метод. Тестовый метод подобен методу образцовых сигналов только вместо образцовых сигналов на вход средства измерений подают сигналы, являющиеся известными функциями образцовых величин и измеряемой величины. Структурная схема средства измерений, работающего по алгоритму тестового метода, показана на рис. 5.4, а. Сначала, когда вычислительное устройство с помощью коммутатора подключает ко входу средства измерений измеряемую величину х, показание t/u запоминается. Затем ко входу средства измерений последовательно подводятся известные функции измеряемой величины и фиксируются соответствующие показания. Если допустима линейно-ломаная аппроксимация реальной градуировочной характеристики средства измерений, то достаточно двух функций: Ai{x) и Aiix).

Из системы уравнений

Уо= ао(/) +а, (ti)x, yi = ao(t2)+at{t2)A{x), У2= ао{(з) + щ{1з)А2{х)

с помощью вычислительного устройства определяют измеряемую величину. Для упрощения решения системы уравнений функции

Блок формирования тестов

Средство измерений

Вычислитель -ное устройство

x+L x