

|
|
Главная -> Понятия метрологии 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 [52] 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 За время паузы между исследуемыми импульсами это напряжение немного возрастает, и изображение спектра каждого очередного импульса несколько смещается вверх и вправо. Под действием нескольких импульсов на экране возникает изображение временного рельефа спектра. Для трех импульсов такой рельеф показан на рис. 8.10, б. По рельефу удобно судить об изменениях спектральной плотности импульсов анализируемой последовательности. Основные характеристики анализатора спектра с ДЛЗ. Спектральный анализ с помощью ДЛЗ происходит за очень малый промежуток времени, определяемый длительностью импульса выходного напряжения ДЛЗ. Предельная его длительность составляет т„, этим же значением можно оценить и время анализа. Метод накладывает ограничения на длительность анализируемых радиоимпульсов. Например, прямоугольный импульс длительности т после преобразования превратится в импульс с ЛЧМ, ширина спектра которого Aio = p.T, т. е. пропорциональна длительности. Заметим, что такая зависимость характерна только для сигналов с большой базой. Поскольку спектр исследуемого импульса с ЛЧМ должен попасть в пределы полосы пропускания цт„ ДЛЗ, то необходимо выполнение условия рт<рт„ или т<т„. Следовательно, длительность исследуемого импульса не должна превышать т„. С уменьшением длительности исследуемого импульса его база резко уменьшается пропорционально т. С уменьшением базы постепенно начинают нарушаться условия, при которых справедливо соотношение (8.3), и форма выходного напряжения ДЛЗ начинает все в большей мере отклоняться от формы огибающей спектральной плотности. Начиная с определенной длительности, эти отклонения настолько велики, что по выходному напряжению уже нельзя судить об огибающей спектральной плотности. Следовательно, диапазон длительностей анализируемых импульсов определяется полосой пропускания ДЛЗ. Так, для промышленного анализатора спектра С4-47 диапазон длительностей составляет 0,4...6 мкс. Рассмотрим теперь особенности спектрального анализа непрерывных колебаний. Как уже указывалось, такие колебания сначала модулируют по амплитуде, превращая их в последовательность импульсов. Если, например, модулирующий импульс прямоугольный, то на экране ЭЛТ изображается его спектральная плотность (рис. 8.10, в). Частоту исследуемого колебания определяют по положению центрального лепестка спектральной плотности на оси абсцисс. Разрешающую способность анализатора можно оценить удвоенной шириной центрального лепестка на уровне 0,707 от максимального. Ширина главного лепестка на этом уровне составляет 0,45/т, так что разрешающая способность равна 0,9/т„. Для повышения разрешающей способности следует выбирать возможно большую длительность импульса, ограниченную значением т„, что соответствует разрешающей способности 0,9/т„. Спектр импульса длительности т„ занимает всю полосу пропускания ДЛЗ, и при изменении частоты исследуемого колебания спектр сместится и выйдет за пределы полосы. Поэтому на практике длительность прямоугольного модулирующего импульса т<;тя, что приводит к некоторому ухудшению разрешающей способности. Боковые лепестки, возникающие на экране ЭЛТ при модуляции прямоугольными импульсами, не несут полезной информации об амплитуде и частоте исследуемого гармонического колебания и лищь затрудняют наблюдение спектра. Поэтому предпочтительны другие формы модулирующих импульсов с меньшими боковыми лепестками, например косинусоидальные, спектр которых показан на рис. 8.10, г. 8.4. СПЕКТРАЛЬНЫЙ АНАЛИЗ С ПОМОЩЬЮ ДИСКРЕТНОГО ПРЕОБРАЗОВАНИЯ ФУРЬЕ Для осуществления такого анализа сначала исследуемый сигнал дискретизируют, а затем с помощью ЭВМ рассчитывают спектр. Остановимся только на особенностях структурной схемы анализатора и погрешностях спектрального анализа. Основные соотношения. Если имеются N дискретных значений сигнала u(iT) (г = 0, .... Л/- 1), взятых в моменты О, Т, (Л/- \)Т (рис. 8.11, а), то эти значения мысленно можно повторить бесконечное число раз, в результате чего получится периодический сигнал, как показано штриховой линией на рис. 8.11, а. Такой сигнал можно разложить в ряд Фурье, совокупность коэффициентов которого С„ = 2 «(гТ) ехр i - \2лп определяет спектр дискретизированного периодического сигнала. Спектральная плотность S {пЩ = Г 2 «(iT) ехр - \2пп . (8.4) u.[{N-l)T] О Т {N-1)7 Зак. 1898 Это соотношение является дискретным преобразованием Фурье, по которому вычисляют спектр. Спектральная плотность дискретного сигнала представляет собой совокупность спектральных составляющих, отстоящих друг от друга на Й = 2л/Г (рис. 8.11, б). Общее число составляющих равно числу отсчетов N сигнала. Особенности структурной схемы анализатора. Погрешности. Квантование сигнала приводит к погрешности, называемой шумом квантования. Эта погрешность ограничивает динамический диапазон прибора значением £>= 101g3-/V2/4 дБ. Для Л/ = 256... ... 1024 отсчетов и п = 8, 10 разрядов двоичного АЦП динамический диапазон может составлять 70...90 дБ. Однако из-за погрешностей при вычислениях, внутренних шумов схемы и некоторого непостоянства периода отсчета он снижается до 60 дБ. Возможны различные варианты построения устройств дискретизации. Как правило, прибор должен обеспечивать непрерывную обработку сигнала без потери отсчетов. Поэтому в простейшем случае сначала в ОЗУ накапливают N отсчетов, а затем в течение паузы происходит их обработка, которая заканчивается к моменту появления очередного отсчета. Расчеты обычно производят по алгоритму быстрого преобразования Фурье, применение которого позволяет на два порядка сократить число операций по сравнению с алгоритмом преобразования Фурье при N> 1000. Из-за значительного времени, необходимого для расчетов, в рассмотренном случае время дискретизации может составлять до сотых долей секунды. Быстродействие существенно увеличивают, используя буферную память, состоящую из двух поочередно подключаемых к вычислительному устройству блоков. Некоторые погрешности обусловлены свойствами ДПФ. Как следует из (8.4), спектр дискретного сигнала периодический с периодом 2л/Т. Следовательно, если период превышает ширину спектра 2о)в, то соседние спектры не перекрываются (рис. 8.12, а), 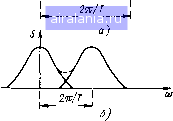 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 [52] 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 0.0107 |