сначала погрешность в первом канале. Предположим, что смещение AUypi мало, тогда согласно рис. 9.5, а, получим

Mypi = MJypi/{dUxi/dt).

В большинстве случаев смещение в основном определяется медленным дрейфом уровня формирования и погрешность Aypi имеет преимущественно систематический характер.

Погрешность под влиянием шумоюго напряжения оценивают соотношением

Muii = Un,[{ti)/{dUx\/dt),

полученным согласно рис. 9.5, б. Соотношение справедливо при выполнении двух условий. Первое заключается в малости шума, а второе состоит в том, что скорость изменений шумового напря жения должна быть малой по сравнению со скоростью изменений напряжения вблизи уровня формирования:

0ш1<

Ош1 =- coS (со) dco

- СКО производной шумового напряжения, 5(ш) - энергетический спектр шума.

Если перечисленные условия не выполняются, то в формирующем устройстве может получиться несколько пересечений уровня формирования (рис. 9.5, в) и возникнут ложные запуски триггера Шмидта. Для устранения повторных запусков используют формирующие устройства с большим гистерезисом. Так, повторные запуски исключаются, если уровень формирования Ui, при котором триггер переводится в исходное состояние при уменьшающемся напряжении, выбрать немного меньше уровня U[.

Общая погрешность, учитывающая влияния обоих каналов,

ЛФ =( Лиф2 -f Wm2) --(Аиф1 -f Ыш1) I

Погрешность можно вычислить по известным характеристикам дестабилизирующих факторов, например по скорости ухода уровней формирования и СКО шумовых напряжений. Если уход содержит флуктуационную составляющую, то ее суммируют с шумом на входе и рассматривают общее шумовое напряжение - приведенный ко входу шум.

При расчете СКО погрешности, обусловленной шумом, в дальнейшем будем считать, что шумовые напряжения в начале и в конце интервала статистически независимы, а следовательно, и независимы погрешности Аш1 и Аш2.

Погрешности за счет запаздывания имеют преимущественно систематический характер, а их значения зависят от элементной базы и могут составлять от единиц до десятков наносекунд. При идентичных каналах эти погрешности в значительной мере компенсируются и в дальнейшем рассматриваться не будут.

В выпускаемых промышленностью приборах перечисленные погрешности отдельно не учитывают, а оценивают пределы допускаемой погрешности: Как это следует из рис. 9.5, г, суммарная погрешность (за исключением погрешности дискретности), обусловленная всеми факторами, влияющими на уровень формирования, в наихудшем случае не может превышать предельного значения Aifп = 0,5(тфl--Тф2), где Тф и Тф2 - длительности фронтов импульсных напряжений в каналах.

Предел допускаемой погрешности измерений временного интервала

Аопг = боп, Тх + Та + 0,5( Тф, + Тфг), (9.6)

где боп[ = боп7- •

Пример 9.1. Пусть требуется измерить период повторения гармонического колебания Ux = UmCos2nft, где Um=\ В; f=l кГц. Вместе с колебаниями на вход триггера Шмидта воздействует шумовое напряжение со СКО аш = 0,1 мВ. Определим СКО результатов измерений, вызванное дискретностью счета и влиянием шумов. Период повторения счетных импульсов Го=100 не, коэффициент деления делителя частоты л=1.

Среднее квадратическое отклонение погрешности дискретизации ад=10С>уб = = 44 НС. Для расчета погрешности за счет шума вычислим производную dujdt в точках формирования импульсов начала и конца интервала. Пусть эти импульсы формируются при пересечении косинусоидой уровня 1/ф=10 мВ, тогда dux/dttv и„2л!.

Обшая погрешность складывается из двух слагаемых, возникающих при формировании импульсов «„ н «к- Поскольку средние квадратическне отклонения слагаемых одинаковы и равны Ош, а значения шумового напряжения в моменты формирования МОЖНО считать статистически независимыми, то среднеквадрати-ческое значение погрешности А/ф составит

аф = ашл/2/У„,2л/я22,5 не.

Общая погрешность при однократном измерении aj- =-уа + (Тф = 49 не.

Как это следует из примера, погрешность за счет шума может доминировать и ограничивать точность измерений. Даже при большом отношении сигнал-шум q ~ и„/с! = 0,707 ]0*, что соответствует 77 дБ, шумовая погрешность все же значительна.

Измерения с многократными наблюдениями как способ уменьшения погрешности дискретизации. Погрешность дискретизации, органически связанная с самой методикой измерений, определяет предельные возможности электронно-счетных изме-

tiI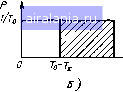

To t,

Рис. 9.6

ригелей временных интервалов. Поэтому в дальнейшем будут рассмотрены различные методы уменьшения этой погрешности. Наиболее простой способ заключается в проведении измерений с многократными наблюдениями.

Рассмотрим сначала случай, когда Гг<Го. Как следует из рис. 9.6, а, при этом измеряемый интервал может занимать различные положения относительно последовательности счетных импульсов, а показания счетчика могут быть О или 1. Пусть положение фронта импульса относительно счетных импульсов случайно и в пределах периода То счетных импульсов подчинено равномерному закону (рис. 9.6, б). Тогда счетчик зафиксирует 1, если смещение ti лежит от То - Тх до То- Следовательно, вероятность появления одного импульса Pi=P{To-Txt\To]=Tx/To, и по экспериментально полученной оценке вероятности можно оценить интервал Тх-

Как следует из рис. 9.6, а, результат каждого измерения - дискретная случайная величина у - может принимать значения У1 = 1 с вероятностью Pi и у2 = 0 с вероятностью 1-Pi.

Пусть в результател опытов счетчик т раз зафиксировал I и п - т раз 0. Оценка Pi вероятности Pi определяется по относительной частоте повторения появления единицы:

й m 1 v

где у, - показание счетчика (О или 1), полученное в i-м опыте.

По дисперсии ар, оценки Pi можно найти погрешность дискретности при многократных измерениях: al - opjTl. Из (3.22) следует, что 01 = 0 /п. Дисперсию случайной величины у рассчитаем по известному из теории вероятностей соотношению

:=2(у.-у) Р.