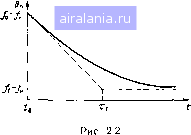ности Qn{t). обусловленная прогревом средства измерений после его включения в сеть. На рис. 2.2 показана возможная зависимость погрешности установки частоты f{x) измерительного генератора от времени, аппроксимированная функцией

е„(/)=f(/)-f„(/о-

-/,)ехр[-(/-/в)/тт],

где f„ - номинальное значение частоты, устанавливаемое по шкале прибора, fo - значение частоты в момент включения, fi - установившееся значение частоты, Тт - эквивалентная тепловая постоянная времени, - момент включения прибора в сеть. Экспериментальная зависимость Q„{t) может описываться и более сложным образом, например суммой нескольких экспонент и линейной функции.

Изменение средней температуры средства измерений при его прогреве может достигать нескольких десятков градусов, что приводит к значительным изменениям систематической погрешности. Если измерения необходимо производить до окончания прогрева средства измерений, то систематическую погрешность можно учесть с помощью ранее полученной зависимости 9„(/) для данного средства изменений. Как правило, эти зависимости для разных экземпляров средств измерений имеют значительный разброс, поэтому использовать некоторую среднюю зависимость для любого экземпляра средств измерений данного типа обычно нецелесообразно.

В большинстве случаев измерения рекомендуют производить по окончании полного прогрева средств измерений. Необходимое время прогрева указывают в паспортных данных.

Изменения внешней температуры также вызывают появление систематической погрешности. Из-за большой тепловой постоянной времени прибора, которая может достигать десятков минут, он оказывает сглаживающее действие по отношению к колебаниям внешней температуры. Быстрые изменения фильтруются и не влияют на среднюю температуру прибора, а медленные колебания температуры среды изменяют его среднюю температуру и, следовательно, вызывают изменение систематической погрешности.

Влияние медленных колебаний температуры на систематическую погрешность можно учесть с помощью приближенного соотношения:

где Кт - постоянный коэффициент; Т° - значение температуры в данный момент: 7S - номинальное значение температуры, при которой температурная погрешность 6т отсутствует.

Прогрессирующая во времени систематическая погрешность Опр() обусловлена постепенным изменением параметров элементов схемы вследствие старения. Это медленный процесс, приближенно описываемый линейной зависимостью

где Кс - постоянный коэффициент; t - время; tn - время проведения последней поверки средства измерений, при которой систематическая погрешность была исключена. Исходя из допустимого значения погрешности бпр и скорости ее изменения, выбирают периодичность поверки.

Математическая модель случайной погрешности. Быстрые флуктуации e{t) определяют случайную погрешность, которую приближенно описывают эргодическим случайным процессом с нулевым математическим ожиданием. При проведении измерений с многократными наблюдениями эта составляющая проявляется в виде случайной величины, принимающей значения £, = е(/,), взятые в моменты /,{/=1,2, п) проведения наблюдений. Значения е, обычно можно считать статистически независимыми.

Отсчитываемые по прибору значения измеряемой величины, а следовательно, и значения е, погрешности всегда содержат определенное число значащих цифр. Поэтому погрешность может принимать конечное число значений и, строго говоря, является дискретной случайной величиной. Однако математическое описание таких величин неудобно, и погрешность принято считать непрерывной случайной величиной.

Наиболее полной характеристикой случайной погрешности являются функции распределения. В дальнейшем будем использовать дифференциальную функцию распределения, называемую также плотностью распределения вероятностей р{г) или сокращенно плотностью вероятности. По известной плотности вероятности можно определить вероятность пребывания случайной погрешности в заданных границах от А„ до Лв:

А»

Рд = Р{Л„<Е<Д4 = Sp(e)de. (2.2)

А»

Для плотностей вероятности, описываемых симметричными относительно начала координат функциями, нижнюю Лн и верхнюю Ав границы погрешности также выбирают симметричными (рис. 2.3, а).

Симметричные границы обозначим одним символом Лвн - положительной величиной. Верхняя и нижняя границы погрешности Лв = Дан Дн=-Двн или ±Двн. Для задзнного закона рас-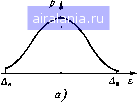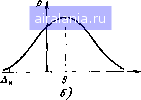

4, Л

Рис. 2.3

пределения вероятность однозначно зависит от границ погрешности и возрастает с их увеличением.

Если =1> то реальные погрешности не могут превышать границ Лв = Лп и Л„=-Дп или ±Дп. Погрешность Дп будем называть предельной.

По результату измерений и границам погрешности оценивают интервал, в котором с заданной вероятностью Яд лежит истинное значение X измеряемой величины. Подставив в (2.2) е = х - Х, получим Рд =Р{х -Двн< Дви}. Следовательно,

вероятность Рд соответствует вероятности пребывания истинного значения на интервале от х -Двн до х + Дв„. Поскольку общая погрешность Д = 6 + е, то ее плотность вероятности можно определить, сместив график /?(е) на 6 (рис. 2.3,6). В данном случае нижнюю Д„ и верхнюю Дв границы интервала, в котором с вероятностью Рд лежит погрешность, выбирают симметрично относительно математического ожидания, поэтому Д„Дв.

К описанию погрешностей плотностью вероятности прибегают сравнительно редко, поскольку для получения Ра приходится прибегать к интегрированию или использовать табличные интегралы, а само экспериментальное определение плотностей вероятности сопряжено со значительными затратами времени.

Числовые характеристики погрешности. Во многих случаях погрешности вычисляют по их числовым характеристикам: математическому ожиданию и центральным моментам. Математическое ожидание погрешности

Л}[Д1 = Д = J Др(Д)Д = 9

(2.3)

равно систематической составляющей.

Центральный момент второго порядка, называемый дисперсией,

f {A-efp{A)dA= ] epie)de,

характеризует рассеяние погрешностей относительно математического ожидания - систематической погрешности. Дисперсия