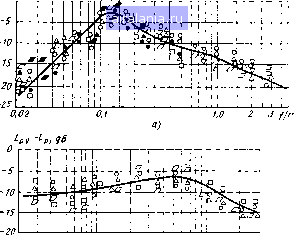2 J 5 67890,1 2 3 11 56 7891,0 2 f/n

Рис, 7.7. Обобщенный относительный спектр:

а - процессов выпуска и впуска; 6 - корпусного шума; • - шум впуска; О - шум выпуска

полученные на основе обработки экспериментальных данных (рис. 7.7). Для оценки уровня шума впуска и выпуска служит экспериментальная кривая (рис. 7.7, а). Однако расчет шума впуска с помощью этой кривой можно проводить лишь до частоты / = 1000 Гц. На более высоких частотах результаты расчета будут получаться несколько завышенными по сравнению с экспериментальными. Это объясняется тем, что характер процессов шумо-образования на впуске и выпуске на высоких частотах отличается более существенно, чем на низких. В итоге совместить полностью кривые спектров шума впуска и выпуска не удается.

На высоких частотах для шума впуска появляется дополнительная ветвь (ниже кривой, показанной на рис. 7.7, а). Для практических расчетов эта ветвь имеет небольшое значение, что позволяет использовать общий обобщенный спектр до частоты 1000 Гц.

Определение спектральных составляющих Lpv незаглушенных источников впуска и выпуска по рис. 7.7, а осуществляют следующим образом. Предварительно по номограмме рис. 7.6 находят величины Lp. Затем для любой среднегеометрической частоты /opv и частоты вращения вала п по рис. 7.7, а получают значение Lp - Lp, откуда находят Lpv, поскольку величина Lp уже определена. Повторяя расчет для каждой октавной полосы частот, получают исходные спектры звуковой мощности шума выпуска и впуска двигателя. Аналогичным образом определяют спектральные составляющие корпусного шума по рис. 7.7, б. 222

Пример. Требуется рассчитать максимальную суммарную звуковую мощ ность незаглушенного выпуска, впуска и корпусного шума и соответствующие октавные спектры звуковой мощности этих источников для двигателя, имеющего рабочий объем цилиндра = 0,2 л, е = 7,6 при частоте вращения коленчатого вала п = 5000 мин"-. По кривой / (см. рис. 7.6) находим обобщенные суммарные уровни звуковой мощности Lp - 20 lg Уд = 147 и 135 дБ соответствен ио для выпуска и впуска. По кривой 2 получим обобщенный суммарный уровень звуковой мощности корпусного шума Lp - 20 lg s = 93 дБ. Суммарные уровни звуковой мощности источников следующие: для выпуска

Lp = (Lp - 20 lg Vb) + 20 lg Vu = 147 -f 20 Ig 0,2 = 133 дБ;

для впуска

Lp = (Lp - 20 lgVb)+20 IgVb

для корпусного шума „ , on , 7 «

Lp = (Lp - 20V lg e) = 93-f-20 lg 7,6

135-f-20 lg 0,2 =121 дБз

= 110,6 дБ.

,e пягтоты * , , соответствующие средним геоме-Рассчитаем безразмерные частоты fcp v/n- определим искомые вели-

трнческим 4acTOTaM/opvoktabh«x полос- и по ниже (в чи-

bilP РчеГеГчГнТ а:наменате - экспериментальные).

. /л OA

f ср v

fcp v

Lpv - Lpv • .

0,025

-20 ИЗ

250 500 0,05 0,1 Выпуск

-12 121

ИЗ 120

Lpv - i-P Lpv . . •

Lpv - bp Lpv

-20 101 105

- 11 99,6

-12 109

4 129 127 Впуск -4 117 117,5

95:5 96

107,5 Корпусной шум -10 -О -5 100,6 101,6 103Л -963" 99,7

4000 0,8

-12 121

-6,5

m,\

101,5

-7,5 103,1

8000 1.6

- 15,5 118,5 116

-11,5

99,1

100,5 95,5

Принимая во внимание простоту расчета и удовлетворительное совпадение его результатов с экспериментальными данными, рассмотренную методику можно рекомендовать для предварительной оценки ожидаемого уровня шума, создаваемого двигателем мотоцикла.

7.3. ФИЗИКО-МАТЕМАТИЧЕСКИЕ МОДЕЛИ ГЕНЕРАЦИИ ШУМА НЕЗАГЛУШЕННЫМИ ИСТОЧНИКАМИ

Остановимся кратко на существующих моделях расчета уровня шума впуска и выпуска двухтактного карбюраторного ДВС. Теоретический расчет при отсутствии гпутт&л&\{ сводится к расчету шума, создаваемого пульсирующей составляющей источников [45]. Звук генерируется при резком вытеснении некоторого объема газа в окружающую среду или при всасывании соответствующего обътг воздуха из окружающей среды (у среза выпускного или впускного патрубка). Для спектров шума впуска

и выпуска характерна (см. рис. 7.1) ярко выраженная низко-и среднечастотная часть. На высоких частотах спектральные составляющие быстро убывают. Поскольку размеры источников невелики, то для существенной части спектра оказывается справедливым неравенство

(7.11)

где d - характерный размер источника; % - длина волны излучаемого звука.

В этом случае конкретная конфигурация излучателя не имеет значения и реальный излучатель может быть заменен моделью пульсирующей сферы. Для более высоких частот применяют модель пульсирующего поршня. Однако обе эти модели не учитывают вихревой составляющей, порождаемой срывом вихрей при обтекании потоком фасонных элементов газовых трактов. Теория расчета вихревых составляющих для двигателя в настоящее время до конца не разработана, поэтому для их определения используют полуэмпирические методы, подобные методам, изложенным в предыдущем подразделе.

В области низких и средних частот вихревая составляющая невелика, поэтому идеализация реального источника пульсирующей сферой как наиболее простая в математическом отношении наглядно поясняет процесс образования основных составляющих, дает результаты, близкие к данным эксперимента. В связи с этим рассмотрим подробнее процесс образования шума этим типовым идеализированным источником. Примем, что пульсирующий шар. малого радиуса R находится в неограниченной среде и излучает сферическую синусоидальную волну. Тогда волновое уравнение для сферической волны можно выразить через потенциал ф звукового поля в следующем виде;

dff/dr"" + (2/г) d(f/dr - (1/а) d\/dt = О, (7.12)

где г - расстояние, отсчитываемое от центра сферы в направлении ее радиуса; а - скорость распространения звуковых волн в среде; t -текущее время.

Решение уравнения (7.12) для синусоидальных колебаний имеет вид

(7.13)

где А а В - постоянные, определяемые из граничных условий задачи; со - круговая частота; / - мнимая единица; k = (о/а = 2я/Я. - волновое число.

Первый член выражения (7.13) представляет волну, расходящуюся от центра, второй - волну, движущуюся в направлении к центру. Для звуковых волн ограничимся в дальнейшем лишь первым членом выражения (7.13)з

(7.14)

Кан известно, звуковое давление р в среде и радиальная скорость V связаны G потенциалом скоростей следующими зависимостями!

р = р d(fldi = feo рф; V = -dtpldr (7.15)

= (-

где р - плотность среды, в которой распространяются волны.

Полагая, что на поверхности шара (при г = R) радиальная скорость

получим из (7.14) и (7.15) для постоянной

m 1 + jkR

(7.16)

(7.17)

и выражение для потенциала через заданную скорость поверхности шара

Объемная скорость источника

где Qvm == - амплитуда объемной скорости источника; 5 = == 4n/? - поверхность источника.

Выразим через нее потенциал звукового поля

(7.19)

Ф ~ 4ГО- 1 + Ш

(7.20)

Из выражения (7.20) для шара, малого по сравнению с длиной волны (kR < 1 или 2aR < X, так как k = 2я/Я,), получим

Величина R в этом выражении отсутствует, следовательно, действие источника характеризуется исключительно его объемной скоростью или производительностью.

Найдем звуковую мощность, излучаемую источником,

(7.22)

= JdS,

где J - интенсивность излучаемого звука, Вт/м-, S площадь поверхности сферы, окружающей источник, м .

Рис. 7.8. Пульсации объемной скорости Qy, создаваемые источником звука:

1 - реальным; 2 - идеализироваыиым

Интенсивность звука в какой-либо точке звукового поля, в свою очередь, зависит от звукового давления в этой точке и колебательной скорости частит

\Re{p) Re {v)dt,

(7.23)

где Re (р) и (о) - действительные части выражений (7.15) соответственно для звукового давления и скорости; Т - период колебания.

Подставляя потенциал скорости (7.21) в формулы (7.15), а полученные выражения последовательно в формулы (7.23) и (7.22), найдем для звуковой мощности простую зависимость от амплитуды объемной скорости (от производительности источника):

(7.24)

Был рассмотрен процесс излучения сферой простой синусоидальной волны. В действительности волна может оказаться несинусоидальной. Однако любое сложное колебание может быть представлено в виде суммы синусоидальных колебаний, каждому из которых будут соответствовать определенная амплитуда объемной скорости Qvmi и определеннэя звуковая мощность Pi. Для этого случая формула (7.24) примет вид

(7.25)

где индекс i соответствует конкретному синусоидальному процессу определенной г-й частоты. f j

Подставляя (7.25) в (7.1) для уровня звуковой мощности, излучаемой на данной частоте Д, и учитывая, что со = 2л?,, для нормальных атмосферных условий (р = 1,2 кг/м а = 341 м/с) получим

Lpi = 98 + 201g/,Qv,„,.

(7.26)

Из формулы (7.26) следует, что излучаемая звуковая мощность целиком зависит от амплитуды объемной скорости, имеющей место на данной частоте. Последнюю обычно определяют, используя зависимость объемной скорости Qy, которой обладает реальный источник, от времени t (рис. 7.8). Для этого функцию Qy (t) раскладывают в ряд Фурье и находят предварительно коэффици-226

енты ряда Фурье по известным формулам гармонического анализа: г, г.

ai=y-Qv (t) cos (icoot) dt; = J Qv, (/) sin (/©<,/) dt, (7.27)

где To = l o -> период повторения пульсаций реального источника; /о - основная частота пульсаций; ©о = 2д/о - угловая частота.

Искомая амплитуда объемной скорости, соответствующая каждому элементарному гармоническому движению,

Qlmi = al + bb (7.28)

Подставляя значение Qy mt в формулу (7.26), определим уровень звуковой мощности, излучаемой на данной частоте. Несмотря на кажущуюся простоту схемы расчета, определение звуковой мощности гармонических составляющих оказывается весьма трудоемким, что связано с нахождением функции Qy (t) и разложением ее в ряд Фурье. Поскольку обычно реальная функция Qy (t) не имеет конечного математического выражения, все операции приходится осуществлять численными методами с использованием ЭВМ, например методом характеристик. Тем самым затрудняется проведение замкнутого расчета и существенно усложняется анализ конкретного процесса генерации шума.

Для облегчения расчетов можно попытаться заменить реальную зависимость изменения объемной скорости перетекающих газов во времени приближенной идеализированной зависимостью, имеющей конечное математическое выражение. Для этой цели удобно использовать следующую функцию, справедливую для значений О < < т:

Qy(t)Ke"s\nfit, (7.29)

где К - амплитуда; а - коэффициент, характеризующий затухание; р = я/т; т - длительность процесса.

Эта функция представляет собой затухающую синусоиду, типичную для колебательного процесса. Ей присущи также общие признаки, характерные для реальных процессов. Например, из анализа зависимостей, полученных для разных источников, следует, что реальные процессы, несмотря на быстротечность, являются плавными, непрерывными. Кроме того, все полученные кривые не являются симметричными: сначала имеют крутой подъем (более резкое увеличение объемной скорости), затем скругленную вершину и, наконец, менее крутой спуск. Кривая, построенная по уравнению (7.29), также получается плавной и имеет характерный несимметричный вид.

Следует отметить, что можно было бы использовать и другие модели реальных процессов, например, в виде импульсов прямоугольной, треугольной, трапецеидальной формы, колокольный импульс. Однако эти идеализированные функции не обладают