деления положения изображения стрелки (справа), представляющего расположенный слева объект. В используемом здесь способе построения хода лучей любой луч, параллельный продольной оси линзы и проходящий через ее поперечную ось, преломляется и проходит через фокальную точку, а любой луч,

Поперечная ось

Объект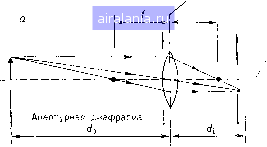

Продольная ось

1=1+1 V f do di

Изображение

Диафрагма поля зрения

Объект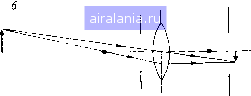

Апертурная диафрагма

Изображение

Диафрагма поля зрения

Апертурная диафра

Изображение

Диафрагма поля зрения

Рис. II.9. Определение оптических диафрагм:

апертурная диафрагма и диафрагма поля зрения открыты; б - апертурная диафраг-

ма закрыта, меньше лучей достигают плоскости изображения; в ния закрыта, часть изображения отсечена

диафрагма поля зре-

проходящий через центр линзы, совсем не преломляется. Край изображения должен быть расположен в точке пересечения двух лучей, как показано на рисунке. Соотношение между фокусным расстоянием f и расстояниями до объекта и изображения - rfo и di дается уравнением тонкой линзы, представленным на рис. II.9. Заметим, что любой луч, идущий от края объекта, при прохождении через поперечную ось линзы преломляется под таким углом, чтобы закончиться на краю изображения стрелки. Если апертура расположена слишком близко к поперечной оси 4-859 49

линзы и закрыта (т. е. «диафрагмирована»), некоторые лучи, идущие от верхней части объекта, блокируются апертурной диафрагмой, как показано на рис. II.9, б. Изображение все еще присутствует целиком, но из-за того, что меньше лучей достигает плоскости изображения, оно менее яркое. Вообще, если закрыть апертурную диафрагму в простой системе тонкой линзы, изображение становится менее ярким.

Если диафрагма поставлена прямо перед изображением и закрыта, блокируются все лучи, заканчивающиеся на краю изображения, как показано на рис. П,9, б, и часть изображения отсечена. Таким образом, диафрагма, расположенная прямо перед плоскостью изображения, - это диафрагма поля зрения, т. е. диафрагма, оказывающая влияние на поле зрения, на часть объекта, которая изображается системой линз и диафрагм.

Апертурная диафрагма определяет способность линзы к собиранию света, или быстродействие объектива. Если апертурная диафрагма закрыта, угловое отклонение Лучей на краю диафрагмы при прохождении их через линзу уменьшается; это видно при рассмотрении рис. П.9, а и П.9, б. Для данного фокусного расстояния угловое отклонение лучей на краю апертурной диафрагмы самое большое, и это отклонение увеличивается, если открыть диафрагму. Поэтому можно соотнести величину углового отклонения лучей в апертурной диафрагме со способностью собирания света системой линза - апертурная диафрагма. Заметим, что если фокусное расстояние линзы уменьшается, а диаметр апертурной диафрагмы остается постоянным, угловое отклонение лучей на краю диафрагмы увеличивается. Таким образом, из двух линз одинакового диаметра, но с разными фокусными расстояниями, та из них, которая имеет меньшее фокусное расстояние, обладает большей способностью к собиранию света. Удобно записать это утверждение в виде отношения fjD, где f - фокусное расстояние линзы, а D - ее диаметр. Чем меньше это отношение, тем больше способность к собиранию света (быстродействие) линзы*.

Геометрия расчета поля зрения (ПЗ) показана на рис. П.10:

Р = ПЗ = 2 arctg id/f) °или рад, (П • 7)

где d - радиус диафрагмы поля зрения (расположенной в фокальной плоскости); f - фокусное расстояние линзы. Заметим, что D - диаметр линзы не влияет на ПЗ линзы. Для примера рассмотрим систему линз обычного 35-миллиметрового объектива с линзами, имеющими фокусное расстояние 50 мм.. Расстояние по диагонали 35-миллиметровой пленки (эффективная диафрагма поля зрения) -41,6 мм, т. е. £=20,8 мм. Поскольку f = = 50 мм, тр

20,8

ПЗ = 2 arctg -= 2x22,5° = 45

* В оптике это отношение называется светосилой линзы. - Прим. пер.

Если поле зрения достаточно мало, тогда применимо приближение tgxwx, и уравнение (II.7) может быть приведено к виду tgP«P = 2d . (II.8)

Расстояние 2d представляет предельный размер диафрагмы поля зрения. В системах дистанционного зондирования расстояние до объекта do много больше, чем расстояние до изобра-

4р(апертура прибора)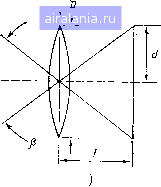

ПЗ = 2Тап- (f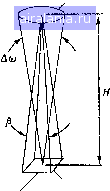

Рис. 11.10. Поле зрения простой-линзы

ГГоверхность Зеипп

Рис. 11.11. Связь апертуры и поля зрения

жения, тогда формула тонкой линзы на рис. II.9, а сводится к виду

1 = l/do-fl/di« l/di.

Это значит, что изображение формируется примерно в фокальной плоскости, (которая содержит фокальную точку) линзы. Диафрагма поля зрения расположена в этой фокальной плоскости. Обычно размеры детектора определяют диафрагму поля зрения и поле зрения датчика в соответствии с уравнением (II.8), поскольку, как мы увидим, iP обычно меньше 1°. Апертурная диафрагма обычно расположена очень близко к самой линзе. В рассмотренных в разд. II.6 многоспектральных сканерах диаметр первичной линзы (или зеркала) определяет размер апертурной диафрагмы.

Отражательная способность, общие положения

Большая часть данных, собираемых системой дистанционного зондирования, получается путем измерения отраженного солнечного излучения. Рассмотрим сначала отражательную способность с математической точки зрения и далее исследуем, какое влияние она оказывает на проблему дистанционного зондирования. Затем рассмотрим, каким образом наблюдаемая в по-4* 51