левых условиях отражательная способность коррелирует с отражательной способностью, наблюдаемой в лаборатории.

Вначале мы должны изучить влияние, оказываемое на измерение излучения полем зрения и апертурой прибора. Если измерительный прибор расположен на высоте Я над поверхностью, от которой необходимо измерить отраженное излучение (рис. 11.11), площадь, видимая прибором, ЛА= (Н), где ip- плоский угол мгновенного поля зрения. Очевидно, что при увеличении Я площадь, определяемая полем зрения, увеличивается. И в то же время апертура прибора с площадью Ар определяет телесный угол А(я на поверхности. Связаны Д(о и Я следующим образом: Л(й=Ар1Н. Таким образом, если предположить, что апертура Ар и поле зрения р фиксированные, то при увеличении высоты Я увеличивается А, а Лео уменьшается. Можно легко показать, что энергия, поступающая в датчик, пропорциональна произведению А(й-<АА= (Ар/Н) (Hfi) =Ар. Поэтому для равномерно освещенного объекта, «заполняющего ЛЛ», энергия, поступающая в датчик, не зависит от Я (если не учитывать влияние пропускания атмосферы).

Функция распределения двунаправленного отражения (ФРДО)

Наиболее фундаментальным свойством, описывающим отражательные характеристики поверхности, является функция распределения двунаправленного отражения (ФРДО), обозначаемая обычно символом f и определяемая в виде dL (9, ф)

/(б.ср; е,¥)-~-що:Г

(Углы, обозначенные символами без штрихов, описывают положение источника излучения, а обозначенные символами со

нормаль к образцу наблюдаемый

Падающий поток

Начальное направление на поверхности образца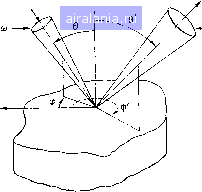

образец

Рис. 11.12. Геометрические параметры, описывающие отражение от поверхности:

6 - зенитный угол, ф - азимутальный угол, ш - телесный угол пучка; символ со штрихом относится к условиям наблюдения (отражения)

штрихами относятся к положению датчика, как это показано на рис. 11.12. Величины м и ю появляются в выражении только тогда, когда они оказывают существенное влиянние на свойства отражательной способности. Обычно со и « в геометрической структуре практического дистанционного зондирования достаточно малы, так что рассматриваемое свойство или величина как функция этих телесных углов значительно не изменяется). ФРДО есть отношение dLjdE в единицах (ср~) и является функцией падающего и отраженного направлений, , r\s\ned,§df обозначенных через 6, ф; 9, ф. Здесь составляющие углы источника или датчика разделены запятой; наборы углов, описывающих падающий и отраженный потоки, разделены точкой с запятой. В литературе /(6,.ф; О, ф) иногда обозначается как р(6,(ф; 6, ф)-Член dU [в единицах Вт/(м2.ср)] - отраженная энергетическая яркость в направлении Э, ф, созданная падающей электрической освещенностью dE (в единицах Вт/м) хорошо коллимированного пучка (параллельных лучей) по

направлению 9, ф. Используя геометрию излучения (рис. 11.13),, получаем энергетическую освещенность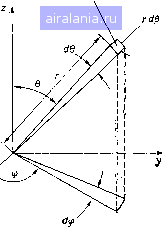

rsinerfy

Рис. 11.13. Геометрия излучения

d£ (6, ф) = L (9, ф) cos Gdco = L (9, ф) cos 9 sin ЫЫц> Вт/м,

(11.9).

где L(9, ф)-падающая энергетическая яркость по направлению 9,.ф через телесный угол (i(o = sin 9с?9ф. Измерение ФРДО достаточно сложно, поскольку точное измерение с?£(9,ф) на поверхности объекта выполнить обычно не удается.

Измерение же L(9, ф) просто. Положение датчика определено представляющими интерес величинами (9, ф). Поток излучения, попадающий в прибор, по терминологии рис. 11.12 определяется формулой

Ф = L (9, ф) Я2р2 (cos 9) = и (9, ф) pMpCos9 Вт. Следовательно,

= -AZ = -Щ Вт/(м.ср)

(11.10)

где vs - выходное напряжение; k - постоянная калибровки датчика. При малых Асо и АЛ эти величины можно считать дифференциалами dca и dA, и уравнение (П.10) дает также величину (6, ф).

Двунаправленная отражательная способность

Другая часто встречающаяся характеристика отражательной способности - двунаправленная отражательная способность, которая выражается в виде

, п А, dl ie,w)cgsqd(o

dpiq,r, е-,ф-)- £(е,ф)созесо -

= /(6,ф,- 0, ф) cosGdco (безразмерная величина). (П.11)

Хотя она используется и измеряется довольно часто, dp не является уникальным свойством образца, а зависит от положения прибора, используемого при измерении, так как величина 4q зависит от cos - проекции телесного угла отражения. Падающий поток определяется характеристиками источника и телесным углом облучения dco. Отраженный в любом направлении полусферы поток, улавливаемый прибором, определяется через rfco - телесный угол отраженной энергетической яркости, жоторый может быть абсолютно отличен от величины dto. Для пользователя данных таких измерений это может вызвать недоразумения.

Взаимность отражательной способности

Свойство ФРДО, полезное при анализе различных типов отражательной способности, устанавливается теоремой взаимности Гельмгольца [9]

/(6,ф; е,ф) = /(е,ф; 0,ф). (11.12)

с физической точки зрения это означает, что источник излучения и датчик можно поменять местами и это не повлияет на величину измеренной ФРДО. Используя рис. П. 12, где индексы обозначают специфические значения параметров 9, и © (с ограничением, что энергетическая яркость по телесному углу падения не изменяется в обоих случаях), применяя уравнение (П.11), можно записать

р(01,ф1,СО1; 02, ф2, ©з) = /(01, ф1, 02, ф2)созе2(В2. (П. 13)

или, меняя индексы местами, перепищем

р(02,Ф2,©2; 01, ©i) =/(02, Фг, 01, Ф1)соз01(В1. (П. 14)

Применяя уравнение (И.12) к членам ФРДО в уравнениях (П.13) и (П.14), получаем

р(01, ф1, ©1,- 02, ф2. ©а) р(02, Фа. щ; Ф1. coi) ПТ1Ч-.

cos02©2 ~ cosBiWi • (I I. 10)

Следовательно, взаимность двунаправленной отражательной способности не столь прямая, как в случае ФРДО, и должна