где g - константа, значение ее принимают обычно между 5 и 10. Для смежного сканирования (т. е. сканирования, при котором линии сканирования касаются друг друга, но не перекрываются) сканирующее зеркало должно сделать 1/р часть оборота; за время продвижения носителя сканера на расстояние рЯ,, т. е. за qH/V секунд, таким образом,

- = -(орад. (11.42).

Зеркало должно вращаться со скоростью 2яК/Я

« = -- Р/ (11.43)

тогда время нарастания

Полоса пропускания системы детектор - усилитель - записывающее устройство

bw = rix, (11.45)

где а - константа, обычно ее значение между 2 и 3. Тогда

в разд. П.5 была рассмотрена чувствительность фотонных детекторов. Исходя из этого, мощность, эквивалентная щуму детектора (МЭШ),

VaTbW 1 А /2р22яК/Я

мэш =

Dx* ~ Dx* [/ apq

Вт. (11.47)

Dx* у т

Необходимо учитывать оптическую эффективность ц. Мощность входного сигнала ------

ДФя = ХаМх ОМц Втл ) (11.48)

Разделив уравнение (П.48) на уравнение (И.47), получим отношение сигнал/шум

ДФ;, VnxgMxDDx* /рАЯт]

МЭШ - AV2gVvjHflD •

Чтобы упростить дальнейшее рассмотрение, примем р = 4, а = 3, =1,5 л; и Т1 = 0,4. Тогда получим

ДФ;, MxDD* /gpAX

МЭШ - 20/VjHf/D

Подробно рассмотрим это уравнение. Заметим, что отношение сигнал/шум увеличивается с увеличением апертуры сканера и с увеличением светосилы оптической системы {D/f). Отношение сигнал/шум также улучшается при увеличении чувствительности квантового детектора и при увеличении имеющегося сигнала {ЛЬ},). Оно зависит от квадрата мгновенного поля зрения сканера и пропорционально ширине спектральной полосы. Заметим, что отношение сигнал/шум обратно пропорционально корню квадратному из отношения ViJH. Это подчеркивает, насколько мы должны посту-литься качеством сигнала, т1тобы получить более высокое :пространственное или спектральное разрешение. Однако заметим, что увеличение отношения скорость/высота {VJH) не оказывает большого влияния на отношение сигнал/шум.

Геометрические характери-:стики. Рассмотрим некоторые геометрические характеристики .многоспектрального сканера, вызывающие искажения в результирующие изображения [16]. Сначала рассмотрим случай с идеальной геометрией, а затем - неидеализированный случай.

На рис. 11.47 и 11.48 приведена геометрия многоспектрального сканера для идеальных условий. Рассмотрим запись /-Г0 элемента разрешения произвольной строки сканирования i. Предположим, что самолет летит строго прямолинейно на постоянной высоте относительно опорной плоскости, называемой уровенной поверхностью (datum), с постоянной скоростью относительно Земли. Координаты самолета Хс, Ус, Zc. Не изменяются также элементы внешнего ориентирования самолета, т. е. отсутствуют тангаж, крен или рысканье. Кроме того, предполагается, что каждая строка сканирования мгновенно записывается.

На рис. 11.48 1р - угловое разрешение сканера внизу по полосе, или по оси X, т. е. это то же самое, что и физическое разрешение сканера. Угол у - действительное угловое разрешение вдоль линии сканирования, или по оси У; оно в конечном счете ограничено физическим разрешением сканера, а также него влияет шаг квантования в процессе преобразования аналог - цифра, которому подвергаются данные. Углы у и ip определяют мгновенное поле зрения (МПЗ). Полный угол сканирования -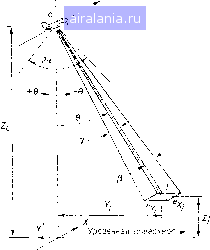

Рис. 11.47. Геометрические параметры сканирования [16]

общее поле зрения (ОПЗ) - равно 2 а. Действительное фокусное расстояние сканирующей системы /. Скорость сканирования выбирается такой, чтобы перекрытие между сканами появлялось при номинальной скорости самолета V. Тогда среднее продвижение для каждой строки сканирования будет (1-S)dX,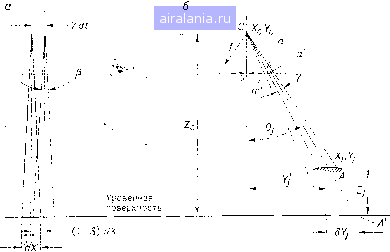

Рис. 11.48. Идеальная геометрия многоспектрального сканера:

а - геометрия вдоль направления полета, б - геометрия поперек направления полета {161

где S - некоторый коэффициент перекрытия, а dX - ширина скана на уроненной поверхности,

dX = Zcp. (11.51)

Здесь Zc - высота самолета над уроненной поверхностью при записи сканером t-й строки сканирования. Размер элемента изображения по направлению вниз по полосе

dX = /p, (11.52)

где / - фокусное расстояние оптики сканирующей системы. Из рис. И.48, а

Vdi= (1 -S)dX. (11.53)

Объединяя эти результаты, получим выражение для X;, которое также равно Хс,

X = Xc = Xo-f (1-5)-рХ.

(11.54)

Здесь Хо - координата по X первой строки сканирования в полете.