Используя рис. 11.48,6, мы можем вычислить наземную координату У/ - расстояние, перпендикулярное к направлению полета,

y; = yc + (Zc-Z)tg9, (11.55)

где У/ - наземная координата точки /; У - координата сканера по оси У в момент записи /-й строки сканирования; Z - превышение точки местности (принятый уровень); Z/ на рис. 11.48,6 заменено на постоянное превышение Z. 6/ - угол сканирования в момент записи

0,.==-, (11.56).

и У/ - положение изображения на круглой цилиндрической поверхности изображения, соосной с линией полета. Величины со-штрихами относятся непосредственно к сканеру.

В действительности эта идеализированная геометрия не реализуема по следующим причинам. Изменение размера элемента разрешения на местности при различных углах сканирования и фактическая запись на круглую цилиндрическую, а не на плоскую поверхность приводят к искажениям, обусловленным углом сканирования. Пренебрежение различиями в превышении: точек объекта над принятой уровенной поверхностью вызывают ошибки, называемые топографическими искажениями. Каждая строка сканирования записывается не мгновенно, что дает искажения, обусловленные временем сканирования. И, наконец, если рассматривать отклонения носителя от идеальной траектории полета, тогда искажения, вызванные изменением элементов внешнего ориентирования датчика, включаются в изображения.

Сначала рассмотрим искажения, обусловленные углом сканирования. Размер элемента в направлении полета, по оси X определяется выражением (см. рис. П.47)

ex. = iZ-Zj)secej. (11.57).

В направлении, перпендикулярном к направлению полета или; вдоль строки сканирования, координата точки местности /

Yj = Yc+(Zc-Zj)tgQj. (II.58>

Если угол дискретизации у достаточно мал, он может быть рассмотрен как дифференциальное изменение угла сканирования 6/, так что

Далее, дифференцируя уравнение (П.58) по 9/, получаем

8Yj = (Zc - Zj) sec2 QjdQj ИЛИ

ey-j = T (2c - Zj) sec2 6- (11.59)

7-859 97

- размер элемента вдоль строки сканирования. Буква 5 здесь относится к смещениям.

На рис. П.49 и 11.50 приведены графики этих уравнений. Здесь размер элемента разрешения на местности представлен в процентах относительно высоты полета над земной поверхностью вдоль осей X и Y соответственно. Большие искажения возникают для больших углов разрешения и больших углов сканирования. И все это не имеет никакого значения для спут-

Си qj

],5-

,1.0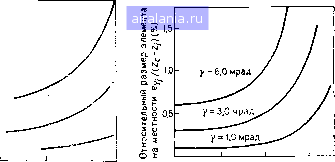

/3 = 6,0 мрад

Р = 3,0 мрад

Р= 1,0 мрад

20 40 60

Угол сканирования в {")

Рис. 11.49. Размер элемента разреиле-мия на местности вдоль оси X [16]

20 40 60

Угол сканирования в (°)

Рис. 11.50. Размер элемента разрешения на местности вдоль оси Y [16]

никовых сканеров вследствие относительно малых у них углов сканирования (в Ландсате полный угол сканирования приблизительно 11°) и малого МПЗ. Эта проблема гораздо серьезнее .для самолетных многоспектральных сканеров.

Дополнительное искажение данных появляется из-за того, что по существу изображение формируется на цилиндрической поверхности, а не на плоскости. Из рис. 11.48,6 видно, что есть различие между некоторым гипотетическим положением изо-бражения, обозначенным а, и его действительным положением а. Результирующее смещение определяется

8у = оа оа f(tgQj - Qj). (11.60)

На рис. П.51 графически показана величина этого смещения относительно фокусного расстояния / для различных углов сканирования. Отметим, что это смещение очень быстро увеличивает-=ся для углов сканирования, больших 45°.

Измерения рельефа земной поверхности могут вызвать явные искажения изображения при больших углах сканирования. Из рис. 11.48,6, видно, что если изображается точка А и предполагается, что она лежит на уроненной поверхности, тогда как в действительности она лежит на некоторой высоте Z/ над этой поверхностью, необходимо изобразить эту точку на уроненной

поверхности как имеющую координату А по оси Y. Тогда действительное смещение на местности, вызванное неучетом рельефа, можно выразить

8Yj = ZjigQj, (II-6)

Zj - превышение элемента над уровенной поверхностью, Q у. результирующее смещение по оси У в масштабе местности. Правильное положение изображения этого элемента будет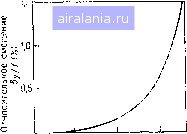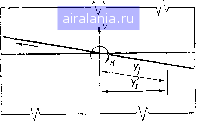

20 40 60

Угол сканирования в (°)

Рис. 11.51. Смещение изображения, Рис. 11.52. Эквивалентное рысканье,, определяемое уравнением (11.60) [16] обусловленное влиянием времени сканирования [16]

В точке а , если элемент сохраняет свое верное положение по. оси У после приведения к уровенной поверхности. Эта ошибка У/ изменяется от О в точке надира (/ = 0) до величины Z/ при угле сканирования 45° и довольно быстро увеличивается для углов сканирования, превышающих 45°. Для устранения ошибки У/ в процесс анализа данных должна быть включена информация о высоте местности под сканером.

Если рассматривать движение самолета во время записи строки сканирования, тогда данные будут записываться так, как это показано на рис. П.52. При этом предполагается, что скорость V самолета постоянна за очень короткое время, требуемое для формирования одного скана. Тогда координата X/ любой точки может быть записана

{П.Щ

где У/ - расстояние на изображении вдоль строки сканирования до точки /; tr--время оборота сканирующего зеркала; / - фокусное расстояние оптики сканирующей системы.

Аномалии в движении платформы датчика показаны на рис. П.53. Если теоретически рассматривать изображение сетки квадратов и наложить эти аномалии платформы на нормальное движение сканера, то результирующее влияние их на это изо-7* 99