бор п измерений, каждое из которых относится к одному из каналов сканера. Предполагается, конечно, что п измерений одного элемента разрешения земной поверхности делаются од-HOjBpeMeHHj). Как отмечалось в гл. I, принято изображать п измерений одной точкой в л-мерном пространстве, называемом пространством измерений. Любая точка в пространстве измерений может быть представлена /г-компонентным вектором измерений X,

где Xi соответствует t-му измерению (измерению в t-й зоне спектра или канале сканера) для данного элемента разреше-" , , 1

Естес-

Рецептор (датчик)

Классификатор (блок принятия решения)

Результат

Рис. II 1.1. Модель системы распознавания образов

ния на земле*. Блок принятия решения, или классификатор, на рис. П1.1 относит вектор измерений к одному из множеств предварительно определенных классов в соответствии с подходящим классификационным правилом. Одна из целей данной главы - описание классификационного правила, обычно используемого при распознавании образов в дистанционных исследованиях.

III.2. Геометрическая интерпретация распознавания образов, дискриминантные функции

Как было отмечено ранее, вектор из п измерений, получаемых многоспектральным сканером для каждого элемента разрешения на Земле, может быть представлен точкой л-мерного пространства. Несколько примеров приведено на рис. П1.2 для случая л = 2. (Многие понятия этой главы иллюстрируются двухмерными примерами. Все они могут быть обобщены для пространств измерений произвольной размерности.)

Когда представляется несколько таких векторов измерений, условно относящихся к одному типу покрытия земной поверхности, но полученных для различных точек Земли, весьма вероятно, что они расположатся скорее в виде локализованного

* В данной главе прописными буквами будут обозначаться векторы, а строчными - отдельные измерения. Часто эти отдельные измерения будут компонентами векторов.

кластера, или оолака точек (рис. 111.3), а не в виде одной точки. Это явление, свойственное для данных дистанционных исследований, является результатом присущих природе случайностей, т. е. случайных изменений в положении листьев растительности, атмосферных условий и даже «щума» аппаратуры дистанционного зондирования. И все же кластеры, относящиеся к определенным типам земного покрытия, обычно более или

• Растительность

Почвз

Вода

Растительность

Почва

вода

Puc.fll.2. Данные в двухмерном про- Рис. III.3. Кластеры точек данных странстве

менее различимы, и в таких случаях возможно связать локализованные области пространства измерений с конкретными типами земного покрытия. Говорят, что такие типы земного покрытия разделимы, все остальные - неразделимы.

Задача проектирования классификатора образов состоит вначале из разбиения соответствующим образом пространства измерений на области рещения так, чтобы каждая область относилась к данному различимому классу (рис. П1.4), и затем из создания такого классификатора, который может отождествлять любой вектор измерений как принадлежащий к классу, соответствующему той области рещения, в которую он попадет. Первая часть этой задачи зачастую оказывается гораздо более трудной, чем это можно предположить по относительно простому случаю, представленному на рис. П1.4, поскольку часто образы, относящиеся к исследуемым классам, несколько перекрываются. Показать, как мы можем эффективно поступать в подобных ситуациях, и есть основная .задача этой главы. Но фактически процесс построения классификатора довольно прост, и мы воспользуемся этим обстоятельством для краткого его описания.

Предположим, что имеем т классов и определены соответствующие этим классам области рещения. Пусть мы можем найти множество функций X, называемых дискриминантными функциями*, которые будем обозначать g\{X), g2{X), gm{X), об-

* В литературе часто употребляют также термины «решающие функции», «разделяющие функции». - Прим. пер.

ладающими тем свойством, что gi{X) имеет большее значение, чем все остальные дискриминантные функции, всякий раз, когда - точка в t-й области решения (позже мы покажем метод

границы jii}-решения

Класс!

Класс 2

Класс 3

Рис. III.4. Области и границы реше-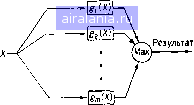

Рис. III.5. Классификатор образов, определенный через дискриминантные функции

определения таких функций). Далее, если мы хотим классифицировать любую точку Хи, т. е. определить, к какой области решения она относится, то все, что нам надо сделать, - вычислить

величины gi{Xu), g2{Xu), .... gm{Xu). Точка Хи принадлежит к классу, имеющему наибольшее значение дискрими нантной функции g. После определения дискриминантные функции могут быть использованы для построения классификатора, как показано схематично на рис. П1.5. Формально мы имеем следующее:

Правило классификации. Пусть со,- обозначает t-й класс. Решаем, что Хац, если и только если gi{X)gj{X) для всех 2, т. (Читается

так: решаем, что X принадлежит к классу i тогда и только тогда, когда gi{X) больше или равно gi{X) для всех классов /=1, 2, т). Действительно, две дискриминантные функции могут иметь равные значения только в точках, лежащих на границах между областями решения. Для этих случаев должно быть определено правило разрешения неопределенности.

В качестве простого примера обсудим ситуацию, изображенную на рис. П1.6. Предположим, нам известно, что область, лежащая ниже прямой х\-А-Х2-2 = 0, соответствует классу 1, а 144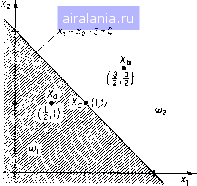

Рис. III.6. простой пример, иллюстрирующий дискриминантные функции