Для удобства записи при условии, что р{Х\ац) является нормальной функцией плотности с математическим ожиданием и г И ковариационной матрицей 2 далее в этой главе будет использоваться обозначение

p{X\(i,i)N{Ui,-Zi). (III.II)

На практике математические ожидания и ковариационные матрицы классов не известны и должны быть оценены по обучающим образам. Пусть Ui и 2г будут несмещенными оценками для Ui и 2/. Ui и 2г тогда имеют вид

/=1.2. (HI. 12)

Oijk = д. 1 2 ~ ~~ f*) / = 1, 2,..., м; fe = 1, 2.....м,

=1 (III.13)

где Qi - число обучающих образов класса i.

Итак, нашей целью является характеристика каждого класса образов с помощью связанной с ним функции распределения вероятностей, которая должна быть оценена по обучающим образам. Предполагая, что «-мерная гистограмма частотного распределения для каждого класса допускает аппроксимацию многомерной нормальной функцией плотности, мы получаем возможность описать классы образов с помощью их векторов математических ожиданий и ковариационных матриц. Это очень компактное и удобное представление по сравнению с представлением с помощью гистограммы (см. задачу П1.13 в конце разд. П1.6).

Мы неоднократно использовали нормальную функцию плотности для аппроксимации частотного распределения, связанного с каждым классом. Достаточно ли разумно делать это на практике? «Многомерное нормальное предположение», что прежде всего было установлено, является хорошей моделью вероятностных процессов, часто наблюдаемых при применении дистанционного зондирования. Кроме того, оказалось, что классификаторы, основанные на этом предположении, достаточно «гибки» в том смысле, что точность классификации не очень чувствительна даже к значительным отклонениям от этого предположения. Наконец, с практической точки зрения эксперименты как с более, так и с менее сложными классификаторами показали, что нормальное предположение обычно обеспечивает хорошее соотношение между характеристикой классификатора (точность) и затратами (быстродействие и сложность классификатора).

Однако при использовании этого предположения особое внимание должно быть уделено двум вопросам. Во-первых, должны быть адекватные обучающие выборки, позволяющие 154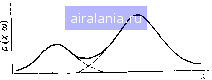

оценить математические ожидания и ковариационные матрицы каждого класса. Если при классификации используются данные п диапазонов длин волн, теоретически минимальное число обучающих образов для класса равно При меньшем числе

обучающих образов ковариационная матрица будет выролден-ной (ее детерминант равен О, и обратная матрица не существует), что делает невозможным вычисление выражения (П1.10). На практике, однако, необходимо иметь по крайней мере \0п обучающих образов и даже лучше ЮОд, чтобы получить хорошие оценки параметров классов.

Второй вопрос, которому необходимо уделить внимание, касается случаев, в которых нормальное предположение отвергается с полной очевидно- Рис. 111.11. Многомодальная функция СТЬЮ. В частности, классы, распределения вероятностей и ее раз-ИМеЮЩИе явно .МНОГОМОДалЬ- деление на подклассы ные функции распределения

вероятностей (функции, имеющие более одного максимума), обычно ие могут быть удовлетворительно аппроксимированы нормальной функцией плотности, являющейся одномодальной с единственным максимумом. Распространенное практическое решение этого вопроса - разделение такого класса на несколько подклассов, по одному на каждую моду действительного распределения, так что функция распределения вероятностей каждого подкласса может быть представлена нормальной функцией плотности (рис. П1.11). Метод выявления многомодальных классов и разделения их на подклассы будет обсуждаться позднее в разделе, посвященном кластерному анализу.

111.6. Дискриминантные функции,

базирующиеся на статистической теории

В разделе П1.2 отмечалось, что проектирование классификатора включает определение набора дискриминантных функций, разделяющих пространство измерений на соответствующие области решения. Вспомним, что дискриминантные функции определяются таким образом, что функция, соответствующая t-му классу образов, имеет в каждой точке пространства признаков соответствующей данному классу, значения, большие, чем значения любой другой дискриминантной функции. Теперь, после введения некоторых важных статистических понятий, мы покажем, как можно применить статистическую теорию решений для нахождения оптимального набора дискриминантных функций.

Прежде всего представим окончательный результат и кратко его обсудим. Предположим, что имеем т классов образов.

Пусть р{Х\ыг)-функция ПЛОТНОСТИ вероятностей, зависящая от вектора измерений X, при условии, что X принадлежит к образам класса /. Пусть р{(Ог) -априорная вероятность класса i, т. е. вероятность наблюдения образа из класса i, независимо от любой другой информации. Обычно используемая стратегия классификации заключается в следующем.

Решающее правило по максимуму правдоподобия. Принять решение Хеш,-, если и только если р{Х\(дг)р{оь) p(Zj(Oj)p(©j) для всех /==1, 2, т*. Значит, чтобы классифицировать образ X, используя решающее правило по максимуму правдоподобия, ЭВМ вычисляет произведения p(Zjcoi)p(©i) для каждого класса и относит образ к классу, имеющему наибольшее значение произведения. Отметим, что набор произведений p{X\oii)p{iOi), 2, т, используемый в этом правиле, образует набор Дискриминантных функций.

В примере игры в кости игрок 2 мог бы воспользоваться решающим правилом по максимуму правдоподобия для максимизации выигрыша. Величина р(Хо>;) соответствует функции распределения вероятностей для пары костей, а р(сог)-вероятность, что игрок 1 выберет для бросания t-ю пару костей (0,5 для каждой пары, если игрок 1 не предпочтет одну пару другой) .

В качестве другого примера рассмотрим задачу дистанционного зондирования, в которой требуется получить поточечную классификацию области, состоящей из растительности, почвы и воды. Наземные наблюдения показывают, что 60% области составляет растительность, 20% - почва и 20%-вода, т. е.

p(coi)=/j (растительность) =0,60 Р(со2)=р (почва) =0,20

р(©з)=р (вода) =0,20

Функции распределения вероятностей р (Х растительность), р(Л[почва), р(вода) можно оценить, если предположить, что каждый класс имеет многомерную нормальную плотность вероятностей, и вычислить математические ожидания и ковариационные матрицы по обучающим данным.

В сельскохозяйственных приложениях априорные вероятности p(©i) могут оцениваться по архивным записям площадей посевов за предыдущие годы, по записи продажи семян или другой информации Министерства сельского хозяйства США, Функции распределения вероятностей p(Xjcoj), связанные с различными сельскохозяйственными культурами, обычно необходимо оценивать по обучающим выборкам.

А теперь перейдем к выводу дискриминантных функций, используемых в решающем правиле no MaiiCHMyM}jTpa бия. Цель последующего материала - ввести читателя в курс

Величина /j(Xlwi). рассматриваемая как функция от аа, называется функцией правдоподобия для класса i или просто правдоподобием. Отсюда название сформулированного решающего правила. - Прим. пер.