крытие классов, подлежащих классификации в пространстве измерений. Практически следствием этого является то, что классификатор, используя доступную дистанционную информацию, неизбежно принимает ошибочные решения, так как часть, образов класса 1 не отличима от образов класса 2, часть образов класса 2 не отличается от образов класса 3 и т. д. Основная цель использования статистического подхода - минимизировать частоту появления таких ошибок, т. е. минимизировать вероятность ошибки.

При условии, что у нас есть стратегия построения классификаторов с минимальной вероятностью ошибки, имеется ряд причин, вызывающих необходимость вычисления для конкретной задачи, соответствующей вероятности ошибки. Во-первых,, вероятность ошибки помогает определить доверительный уровень результатов классификации. Если вероятность ошибки слишком, велика, необходимо, может быть, искать некоторые другие средства или измерения для лучшего разделения исследуемых классов. Кроме того, как мы увидим в дальнейшем, вероятность ошибки может служить критерием при разработке эффективного классификатора.

Чтобы получить интуитивное представление, как получается вероятность ошибки и как ее можно вычислить, возвратимся к примеру с парами игральных костей (см. разд. П1.4). Вы помните, что игра проводится с двумя парами костей, стандартной парой и подправленной парой с двумя дополнительными метками на каждой стороне. Цель игры - «классифицировать» кости, выбранные для каждого бросания, основываясь на сумме выпавших очков. Как видно из рис. П1.9, классы образов в действительности перекрываются. Каждый раз при выпадании суммы от 6 до 12 имеется некоторая неопределенность относительно брошенной пары. Наибольшая неопределенность существует при сумме 9, наименьшая-при суммах 6 и 12.

Предположим, что знакомый со статистикой игрок 2 выбрал стратегию максимума правдоподобия. Предполагая априорные вероятности равными р (стандартные кости) =/? (подправленные кости =0,5, игрок 2 будет следовать правилу: решать «стандартная» всякий раз, когда выброшенная сумма X такая, что p(xстандартная пара)(л:[подправленная пара), и решать «подправленная», если

jt7(xподправленная пара) >p(x[стандартная пара). Заметим, что все суммы 9 произвольно классифицируются как «стандартные». Правило можно переписать и так, чтобы клас сифицировать сумму 9 как «подправленные». В любом случае вероятность угадывания при сумме очков 9 равна 0,5, так как функции распределения вероятностей и априорные вероятности равны.

Какова вероятность того, что игрок 2 при любом бросаний сделает ошибку, следуя этому правилу, если игрок 1 уже выбрал для бросания стандартную пару? Она равна вероятности

И* 163

Того, игрок 1 выбросит сумму очков 10, 11 или 12, так как, следуя правилу, при этих значениях суммы нужно угадывать «подправленная пара». Мы можем записать это так: р (ошибка стандартная) =р(10стандартная)4-р(11 стандартная)-[-р (12 стандартная) =3/36-- 2/36-1-1/36=1/6. Другими словами, приблизительно в одном случае из шести при бросании стандартной пары будут выпадать суммы 10, И или 12, и игрок 2 сделает поэтому ошибочную классификацию. Аналогично, р (ошибка/под-

правленная) = 2p(f подправленная) = 4/36+3/36-1-2/36-- 1/36 = = 5/18.

Наиболее важен, однако, тот факт, что для описанной игры, предполагая использование стратегии максимума правдоподобия, мы можем вычислить вероятность того, что игрок 2 сделает ошибку при любом данном бросании:

р (ошибка) = р (стандартная) р (ошибка стандартная) -f

-\- р (подправленная) р (ошибка подправленная) =

= (1/2x1/6) -f (1/2x5/18) = 2/9. (III.25)

Другими словами, (вероятность, что игрок 2 делает ошибку) = (вероятность, что игрок I выберет стандартный набор) X (вероятность, что игрок 2 делает ошибку при условии, что выбран стандартный набор) + (вероятность, что игрок 1 выберет подправленный набор) X (вероятность, что игрок 2 делает ошибку при условии, что выбран подправленный набор).

Или же мы можем интерпретировать этот результат как среднюю частоту ошибочных решений игрока 2 при многих последовательных бросаниях. Поскольку принятая стратегия находится в соответствии с рассуждениями, приведенными в пре-дыдушем разделе, мы знаем, что вероятность ошибки при этом минимальная из всех возможных.

Рис. III. 13 иллюстрирует такой факт: вероятность ошибки близко связана с областями, лежащими ниже функции распределения вероятностей в зоне перекрытия. Эти области заштрихованы и разделены границей решения по максимуму правдоподобия. Возвращаясь к уравнению (III.25), мы видим, что правая заштрихованная область соответствует члену р(ошиб-ка стандартная), а левая - члену р (ошибка j подправленная). Для вычисления общей ошибки нужно просто сложить эти области с учетом соответствующих априорных вероятностей. Таким образом, чем больше эти области, тем больше вероятность ошибки, и наоборот. Так как мы хотим иметь классификатор с минимальной вероятностью ошибки, при разработке классифи-.катора всегда нужно стремиться минимизировать эти области. Мы будем широко использовать эту идею при более общем обсуждении вероятности ошибки.

Предположим, что имеем одно доступное дистанционное измерение и хотим сделать разделение двух классов покрытия

р (х\ стандартные кости)

р [х\подправленные 1--1 кости)

1 2 3 4 5 6 7 8 9/ Ю И 12 13 14 15 16 X Граница решения

Рис. 111.13. Заштрихованные области отражают вероятность ошибки а б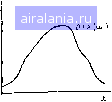

р{шг)р(.х\ы2)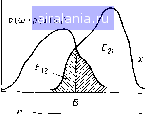

11 1-"2

Рис. 111.14. Связь между вероятностью ошибки и перекрытием функций плотности классов:

с - функции плотности вероятностей для гипотетических классов покрытия Земли; б - область перекрытия (заштрихованная) отражает вероятность ошибки

земной поверхности, имеющих функции HvIOthocth вероятностей р{х\&\) и р(хсо2), как показано на рис. III.14,а. Умножая значение кривых в каждой точке на соответствующие априорные вероятности и представляя результаты на общем графике, получаем рис. 111.14,6. Граница рещения по максимуму правдоподобия проходит через точку В, в которой кривые пересекаются. Вероятность ошибки дается выражением

Ря = £12-Ь£21, (III.26

ii2 = J р (©а) р (х I ©г) dx.

р(щ)р{х\щ)(1х.

Составляющая ошибки £12 - это вероятность, связанная с классификацией наблюдений в класс 1, когда они в действительности принадлежат классу 2; £21 - вероятность классификации наблюдений, принадлежащих классу 1, в класс 2. Кроме того, -£12 и £21 соответствуют «зонам перекрытия», заштрихованным на рис. 111.14,6.

Соотношение (III.26) справедливо для любой двухклассовой задачи в случае применения решающего правила по максимуму