среДнее значение для всех пар классов, т. е.

1 т т

/=1 /=1

широко разнесенные классы уже не оказывают большого влияния на среднее (рис. III.21). В данном случае типичные значения расстояния J-M, соответствующие заданным значениям вероятности ошибки, затабулированы [6]. Мы убеждаемся, что /i3 и /23 не слишком увеличивают среднее значение, так что [Хс, Ха) - это и есть выбранный поднабор признаков.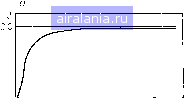

Нормализованное расстояние

Нормализсзанное расстояние

Рис. 111.20. J-M расстояние и вероятность правильного распознавания как функции нормализованного расстояния:

a - J-M расстояние /. б - вероятность правильного распознавания Р (в процентах)

Преимущества насыщающего поведения J-M расстояния были подтверждены экспериментами. Эксперименты показали также, что насыщающаяся функция дивергенции может дать аналогичные результаты и несколько легче вычисляется (т. е. требует меньше машинного времени) [6]. Эта насыщающая функция, названная преобразованной дивергенцией и обозначенная определяется выражением

DT.. = 2 [ 1 - ехр , (111.39)

где Dij - обычная дивергенция, определенная ранее [уравнение (П1.30)]. Интересно сравнить форму этого выражения с уравнением (И1.36). Именно эффект насыщения члена с отрицательной экспонентой в обоих выражениях делает эти меры расстояния полезными для задач многоклассовой классификации.

Как мы видели, вычисление попарной разделимости (Dcp или /ср) для всех пар классов - одна из возможных стратегий при отборе лучших признаков в многоклассовой задаче. Возможна и такая стратегия. Выбирайте тот набор признаков, для которого минимальная разделимость между любой парой классов максимальна. Другими словами, выбирайте набор признаков, который лучше всего разделяет наиболее трудно разделимую пару классов.

В простом примере, приведенном выше (см. рис. П1.19, П1.21), получилось так, что эта стратегия выбирает нужный

набор признаков (хс, Xd) независимо от использованной меры разделимости. Эта стратегия представляется разумной при отборе признаков во многих практических задачах. Хотя она не строго совместима с (байесовской) стратегией минимального среднего риска, на которой базировалось получение дискриминантных функций, этой стратегии часто придерживаются в случаях, когда требуется точное разделение нескольких трудно разделимых классов.

Прежде чем закончить обсуждение статистической разделимости и вероятности ошибки, кратко укажем точные соотноше-

Предполагается.что

J,2 = 0,50 J,3 = 1,90 J23 = 1,90

Ре = 0,20 Ре = 0,01 Ре = 0,01 Pe,ave= 0.07

® ®

7,2 = 1,30 Ре = 0,07

/3 = 1,70 Ре = Q03

23 = 170 Ре = 0,03

/ave= 1.57 Pe ave= 0,04

Рис. 111.21. J-M расстояние отбирает наилучшие признаки для данного примера многих классов

ния между введенными мерами разделимости и вероятностью •ошибки. Конечно, для данного значения дивергенции или J-M расстояния между двумя классами хорошо было бы указать конкретное значение вероятности ошибки. Это невозможно, но мы можем определить границы вероятности ошибки. В частности, можно показать [7, 8], что если D - дивергенция и / - расстояние Джеффриса - Матусита между двумя классами с равными априорными вероятностями, то вероятность ошибки ограничивается в соответствии со следующими выражениями:

l/4exp(~D/2)<P£. и 1/16(2-P)2p l l/2(l-f 1/2Р),

Вновь мы убеждаемся, что свойства J-M расстояния больше соответствуют нашим требованиям, поскольку в этом случае мы можем ограничить вероятность ошибки сверху и снизу. Дивергенция имеет только нижнюю границу.

На этом заканчиваем обсуждение проблемы оценки ошибки классификатора. Подробно рассмотрев отбор признаков как область применения оценки ошибки, перейдем к рассмотрению отчасти более общего подхода к определению признаков, наилучшим образом подходящих для классификации. 176

111.91 Выделение признаков

Термин «признак» использовался в предыдущем разделе для обозначения одного из измерений образа. В более общем смысле признаком можно называть некоторый объем информации, содержащейся в измерениях, который полезен при принятии решения о принадлежности образа к тому или иному классу. Исходные измерения могут содержать много «информации», не приносящей пользу в процессе классификации и даже иногда затрудняющей его. Для нас это - дезинформация, и в дальнейшем будем называть ее просто шумом. Грубо говоря, выделение признаков выполняет две функции: 1) отделение полезной информации от шума и 2) сокращение размерности данных с целью упрощения вычислений, выполняемых классификатором. Последняя функция - та же самая функция, которая выполняется при отборе признаков, который является, как мы увидим, частным случаем выделения признаков.

Чтобы лучше понять, почему важно сокращение размерности, рассмотрим ее влияние на количество вычислений, необходимых для классификатора по максимуму правдоподобия при использовании многомерных нормальных статистик. Принимая во внимание, что время, необходимое для выполнения умножений, дает подавляющий вклад в общее время каждой классификации, время классификации грубо пропорционально п{п-\--j-l), где п - размерность данных (число используемых признаков). Раньше в большинстве работ по дистанционному зондированию использовались четыре «лучших» признака 12-ка-нальной многоспектральной сканерной системы. Поскольку (4X5) : (12X13) =0,13, для классификации по четырем признакам требуется только 13% времени, необходимого для классификации по всем 12 многоспектральным измерениям сканера. Таким образом, при использовании блока выделения признаков может быть получено значительное сокращение стоимости классификации. Конечно, необходимо также учесть стоимость процесса выделения признаков.

До сих пор мы предполагали, что дискриминантные функции вычисляются блоком принятия решений прямо по вектору измерений X. Согласно модели системы (см. рис. П1.1) это означает, что выход с рецептора поступает непосредственно на классификатор. Теперь мы изменим модель, добавляя блок выделения признаков между рецептором и классификатором (рис. III.22). Обозначим /-й признак г/,-. Если всего имеем т признаков, определим вектор признаков

12-859 177