кой набора данных и математическим ожиданием кластера, к которому данная точка нринисана. Таким образом, при минимизации СКО в качестве критерия кластеризации мы стремимся отнести точки к кластерам так, чтобы кластеры имели наибольшую возможную «плотность».

Другой метод определения критерия кластеризации связывается с определением рассеяния точек внутри кластера 5 и определением рассеяния кластеров Sb (межкластерное рассея-

Начало ,. - .....

Рис. III.26. Основной алгоритм .. кластерного анализа

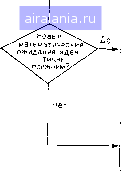Вычислить разделимость кластеров

-Стоп

Установить центры кластеров равными новым математическим ожиданиям

пне). Цель - минимизировать 5 при одновременной максимизации Sb- Очень интересен результат, что этот критерий идентичен минимизации критерия суммы квадратов ошибок [13].

Теперь на этой основе приступим к рассмотрению кластерного алгоритма, схема которого приведена на рис. III.26. Алгоритм работает следующим образом:

1. Выбрать с векторов в качестве начальных «кластерных центров». Mi (i=l, 2, с). Выбор произволен, но все начальные кластерные центры различны. Число центров кластеров

должно оыть задано аналитиком данных; последствия выбора числа центров обсудим ниже.

2. Отнести каждый вектор набора данных к ближайшему центру кластера. Этот шаг требует спецификации меры межточечного расстояния (обычно евклидова расстояния).

3. Вычислить векторы математического ожидания для данных, отнесенных к каждому кластеру. Обозначим математические ожидания через Mi (i=l, 2, с).

Начальные центры кластеров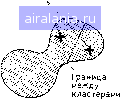

Математические ожидания кластеров а„а"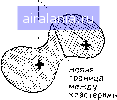

Математические ожидания кластеров в„б"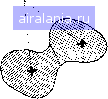

Математические ожидания кластеров в„в" не изменились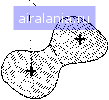

Рис. III.27. Последовательность итераций кластеризации

4. Если новые математические ожидания кластеров идентичны центрам кластеров, то перейти к шагу 5. Иначе, установить Mi=Mi (i= 1, 2, с) и вернуться к шагу 2.

5. Кластеризация закончена. Исследовать разделимость полученных кластеров. Это требует использования меры расстояния между кластерами (возможно, преобразованной дивергенции) .

После каждого повторения шагов 2, 3 и 4 центры кластеров перемещаются так, чтобы уменьшались СКО. Так как СКО ограничена снизу нулем, нет опасности зацикливания, алгоритм обязательно сходится.

На рис. П1.27 приводится пример работы алгоритма на двухмерном бимодальном наборе данных. Рис. ПТ27, а представляет разбиение набора данных на два кластера-кандидата

при произвольном выборе центров кластеров. Математические ожидания данных этих кластеров-кандидатов становятся новыми центрами кластеров, как показано на рис. 111.27,6, и переназначение данных дает новое разбиение. Алгоритм работает, пока математические ожидания кластеров (рис. III.27, г) при очередном разделении совпадают с центрами кластеров, давшими это разделение. На этом процесс заканчивается. Хотя в данном примере требуется всего несколько итераций (число повторений по петле цикла на рис. III.26), на практике для получения окончательного разбиения выполняются десятки и даже сотни итераций.

Цель шага 5 алгоритма - выяснить, действительно ли полученные кластеры разделимы и нет ли среди них расположенных слишком плотно друг к другу в пространстве измерений, что создает излишнее разбиение набора данных. Такой анализ разделимости необходим, так как ранее мы отмечали, что в шаге 1 аналитик данных сам задает число кластеров, подлежащих выделению, и обычно он может лишь дать квалифицированное предположение о соответствующем числе; итеративная часть алгоритма, как он описан, не предусматривает регулировки этого числа.

Таким образом, лучше сначала предположить завышенное число кластеров и затем, в шаге 5, суммировать излишние кластеры после окончания итеративной части алгоритма. Это может быть сделано путем вычисления межклассовых расстояний и объединения тех кластеров, разделимость которых не превосходит некоторую предварительно заданную величину. Порог для объединения должен быть установлен достаточно небольшим, чтобы результирующие составные кластеры не имели многомодальных функций распределения вероятностей.

Некоятролируемый анализ

Когда мы характеризуем множество данных дистанционных измерений путем разделения пространства измерений (или пространства признаков) на неперекрывающиеся области решения, мы фактически определяем спектральные классы, т. е. классы, которые разделимы благодаря различиям многоспектральных свойств соответствующих типов земного покрытия. Дистанционные Исследования успешны потому, что во многих случаях спектральные классы совпадают с информационными классами, т. е. классами покрытия земной поверхности, имеющими определенный смысл (виды сельскохозяйственных культур, основные категории землепользования, типы почв и т. д.). В данной главе было рассмотрено два различных метода установления спектральных классов. Первый метод, использующий обучающие выборки для получения спектральных характеристик информационных классов, называется контролируемой классификацией, так как аналитик данных в определенном смысле контролирует получение границ решения, выбирая обучающие