ГЛАВА If

ПРИНЦИП ДЕЙСТВИЯ ДВУХЭЛЕКТРОДНОЙ ЛАМПЫ или ДИОДА

Двухэлектродную лампу или диод можно считать родоначальницей всех электродных ламп и поэтому полное понимание принципа действия ее значительно облегчит нам в дальнейшем изучение ламп других типов.

В своей простейшей форме диод состоит из металлической нити, накаливаемой электрическим током, и окружающего ее металлического цилиндра, причем оба эти электрода находятся j в высоковакуумном бал- лоне. Давление внутриу, баллона, обычно, на-° столько мало, что сред- няя длина свободного пути электрона (т. е путь, пробегаемый в среднем электроном от одного столкновения с молекулой газа до другого) во много раз больше расстояния .между электродами, так что влиянием остатков газа на работу лампы можно пренебречь.

Для того, чтобы воспроизвести статическую характеристику лампы, применяют схему, изображенную на рис. 1 *.

Здесь А и Л" обозначают соответственно анод и катод (нить) диода. Анодная батарея Ба, обычно, состоит либо из сухих элементов, либо из аккумуляторов малой емкости. V - вольтметр, а тА - миллиамперметр. Изменяя напряжение батареи 6, мы можем определить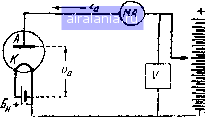

Рнс. 1

4 !

Рис. 2

зависимость анодного тока i„, отсчитываемого по миллиамперметру, от напряжения v, отсчитываемого по вольтметру. В связи с этим следует заметить, что ввиду падения напряжения в миллиамперметре отсчет по вольтметру V не дает точного значения v, но разница эта обычно очень мала.

На рис. 2 приведена типичная характеристика диода с нитью из чистого вольфрама, представляющая графически анодный ток как функцию анодного напряжения*.

Когда анод находится под положительным по отношению к нити напряжением, то количество электронов, которые достигают анода, зависит от величины этого положительного напряжения. Из характеристики видно, что с повышением -Уд анодный ток г„ достигает некоторого определенного значения (точка С на рис. 2), за которым дальнейшее повышение анодного напряжения не вызывает заметного увеличения силы тока. Следовательно, при некотором значении анодного напряжения ток достигает величины насыщения i. Это состояние насыщения наступает тогда, когда все электроны, излучаемые нитью, притягиваются и улавливаются анодом.

С другой стороны, когда напряжение на аноде отрицательно по отношению к нити, то все электроны, вылетающие из нити, отталкиваются анодом и возвращаются на нить; никакого анодного тока нет. В связи с этим очень важно отметить, что электронная эмиссия нити представляет собой вполне определенную величину, которая зависит, главным образом, от температур нити и не зависит существенным образом от напряжения на окружающих электродах. Так как полный ток эмиссии равен г, то электроны, возвращающиеся обратно к нити, очевидно, соответствуют току (4 - 4)-

На первый взгляд трудно понять, почему электроны, представляющие собой отрицательные заряды, не все улавливаются анодом при любом положительном напряжении на нем и почему для улавливания всех электронов необходимо подать на анод некоторое достаточно высокое напряжение. Это обстоятельство обусловливается электрическ м отталкиванием между электронами, находящимися в каждый данный момент в пространстве между нитью и анод м

* Для получения характермстики днода часто удобно пользоваться трех-электродной лампой, у которой аиод и сетка соединены накоротко.

1 . 1

* Принято измерять напряжение на электродах ( напр. у„) по отношению к отрицательному концу нити.

4�95855694

и образующими так называемый простран ственный заряд. Так как одноименные заряды отталкиваются, то электроны, на.ходящиеся на пути к аноду, отталкивают электроны, только что вылетевшие из нити, и ослабляют, таким образом, притяжение, испытываемое ими со стороны положительного анода.

Влияние пространственного заряда на силу анодного тока. Влияние пространственного электронного заряда на установление анодного тока было исследовано теоретически Чайльдом и Ленгмюром, причем первый рассмотрел случай плоских, электродов, а второй как случай плоских, так и цилиндрических электродов.

Случай плоских электродов. Рассмотрим сначала случай плоских электродов (рис. 3), где катод К представляет собой излучающую электроны плоскую поверх-а ность, а анод А в виде параллельной катоду

пластины расположен на расстоянии а от него; будем считать, что расстояние между электродами мало по сравнению с размерами электродов. Примем потенциал катода равным нулю; тогда потенциал анода будет v- Пусть V будет потенциал точки на расстоянии х от катода. Если предположить, что все электроны вылетают из нити с нулевой скоростью, то свою кинетическую энергию они приобретают под действием поля. Следовательно, скорость электронов V (заряд электрона е и масса т) на расстоянии х определяется из уравнения энергии:

•Т 1

Рис. 3

:eV,

(2.1)

где V-потенциал точки х по отношению к катоду.

Пользуясь уравнением Пуассона, связывающим производные от потенциала с объемной плотностькз электрических зарядов и, помня о том, что объемная плотность р заряда, создаваемого электронами, отрицательна, мы можем на-

писать:

52 К

= 4it,o.

(2.2)

Плотность тока г, т. е. число электронов, проходящих в единицу времени через сечение в 1 см можно определить, принимая во внимание, что наступило установившееся состояние и что объемный заряд в любой точке не меняется по величине. Следовательно:

/ = 0V. (2.3)

Подставляя в (2.2) значение v из (2.1) и затем в (2.2)

г

значение р из (2.3), получаем диференциальное уравнение

т 2eV*

описывающее рассматриваемую нами задачу. Интегрирование этого уравнения дает:

дх J

дУ дх

V -У

(2.4)

(2.5)

где Vf, есть потенциал катода, а (j есть градиент потенциала или напряженность электрического поля на поверхности катода. Но мы приняли 1/о = 0. Чайльд и Лэнгмюр сделали предположение, что напряженность поля на поверхности катода также равна нулю. Поэтому уравнение (2.5) принимает вид

= ШсУ -. (2.6)

дх J

Интегрируя это уравнение и вводя пограничные условия нашей задачи: 1/ = 0 при х = 0 и Y=Va при х = а, получаем выражение:

, v:iT/Ziv (27)

- 9я к « а2 . (2.0

которое часто называют уравнением для области пространственного заряда.

Уравнение (2.7) выражено в абсолютных единицах. Если перейти к практическим единицам (i - ajcMP, 1» - в вольтах а-в сантиметрах), то оно примет вид:

2,33 X 10"

Полезно отметить допущения, сделанные нами при выводе этого выражения. Во-первых, мы предположили, что электроны вылетают из нити с нулевой скоростью, что точно не соблюдается. Во-вторых, мы предположили также, что напряженность поля на поверхности катода равна нулю, а это означает, что электрон не испытывает никакой силы, которая заставила бы его двигаться по направлению к аноду. Совершенно очевидно, что нашу теорию следует рассматривать лишь как приближенную.

Более удовлетворительная трактовка была впервые дана Эпштейном (и позднее Фрайем), который принял во внима-

ние максвелловское распределение скоростей электронов, вылетающих из нити. Предварительно Шоттки показал, что влияние начальных скоростей сказывается, главным образом, в том, что они создают в пространстве между электродами область минимального (отрицательного по отношению к катоду) потенциала. Если перемещаться от катода к аноду, то потенциал вначале падает с увеличением х, достигая минимального значения на небольшом расстоянии от катода х, а затем он начинает повышаться, достигая при х - а, т. е. на аноде, значения v. Вследствие этого только те электроны достигают анода, которые вылетают из нити с запасом энергии, достаточным для того, чтобы проникнуть за х. Влияние конечных скоростей вылета электронов на распределение потенциала между электродами показано на рис. 4, где {А) соответствует случаю нулевых начальных скоростей, а (S)- случаю начальной скорости, отличной от нуля. Исследования Шоттки, Эп-штейна и Фрайя показали, что выражение (2.7) является лишь первым приближением и что более точная формула имеет вид;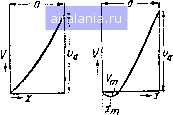

Рис. 4

т (а -д;„)2

(2.9)

к есть постоянная Больцмана, а Т-температура испускаемого нитью «электронного газа>. Более точные дальнейшие исследования показали, что если повышать анодное напряжение, то численные значения V„ и х„ падают так, что при приближении анодного тока к насыщению область минимального потенциала, которая одновременно является и областью, где градиент потенциала и напряженность поля равны нулю, практически совпадают с катодом и тогда условия приближаются к тем, которые были приняты в простой теории Чайльда-Лэнгмюра. При малых V„ и х„ (2.9) очень мало отличается от (2.7). Таким образом, хотя п большинстве практических случаев, в условиях далеких от насыщения, зависимость от степени три вторых оказы-

вается справедливой с достаточной точностью, удовлетворительное теоретическое подтверждение она находит лишь в условиях близких к насыщению.

Случай цилиндрических электродов. Соответствующее выражение для случая, когда нить и анод представляют собой коаксиальные цилиндры, было впервые выведено Лэнгмюром. Обозначим радиусы анода и нити соответственно через а я Ь. Потенциал в точке на расстоянии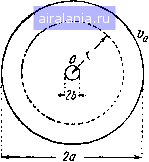

Рис. 5

л? го 30 40 а/ь Рис. 6

г от оси обозначим через V. Тогда вместо уравнений (2.1) (2.2) и (2.3) для плоских электродов мы получим следую щие соответствующие им уравнения:

-гаоЗ = в1/, (2.10)

\ д ( дУ\ / = 2itrpo,

(2.11) (2.12)

где i есть анодный ток на единицу длины цилиндра. Как и в предыдущем случае, эти уравнения можно свести к диференциальному уравнению:

дУ дУ

V еУ

(2.13;

описывающему рассматриваемую нами проблему. Лэнгмюр получил решение этого уравнения в таком виде:

(2.14) 23