Справочник активных фильтров

Наметившийся; в последнее время переход от фундаментальных монографий к справочникам свидетельствует не только о решении проблем практического проектирования активных фильтров, но и о широком распространении последних. Главная трудность создания краткого справонника в условиях существования огромного количества моделей активных фильтров и методик их расчета заключается в выборе тех немногих моделей, которые могут служить промышленными стандартами. Советскому читателю предлагается одна из первых попыток такого выбора, основанная на зарубежной практике внедрения соответствующих разработок.

В справочнике представлен материал по всему комплексу проектирования активных фильтров: от таблип аппроксимации заданных амплитудно- и фазо-частотных характеристик до особенностей настройки. При этом из всех методов реализации выбран •самый простой и распространенный - каскадное построение звеньев фильтров не выше второго порядка. В выборе этих звеньев фильтров хотя и чувствуется личная заинтересованность авторов, но в принципе отражены наиболее широко используемые на практике модели.

Ло данным справочника можно рассчитывать различные типы фильтров (нижних частот, верхних частот, полосно-пропускающие, полосно-заграждающие и постоянных времени замедления и фазы) даже новичкам в этой области. Поскольку авторы максимально упростили расчетные формулы и практически все характеристики фильтров табулированы, то проектирование можно осуществлять при помощи элементарного калькулятора или даже вручную.

Справочник ускорит внедрение в радиоаппаратуру таких малогабаритных избирательных устройств, какими являются активные фильтры.

И. Н. Теплюк

ПРЕДИСЛОВИЕ

То the memory of Al Eskander A prince of a human being

В этой книге представлены упрощеиные методы получения законченных практических конструкций активных фильтров с помощью подстановки численных значений в уравнения. Книга может быть полезна для всех разработчиков фильтров: от новичков до высококвалифицированных специалистов, поскольку в ней уже проведена трудоемкая работа по получению расчетных формул, а сами характеристики фильтров табулированы. В качестве элементов схем используются интегральные операционные усилители, сопротивления и емкости. Расчетные формулы дают стандартные, обычно имеющиеся в наличии номинальные значения элементов.

Отличительной особенностью книги является то, что помимо характеристик филь-ipoB Баттерворта и Чебышева, обычно табулированных, включены также характеристики инверсных Чебышева и эллиптических фильтров. Во всех четырех случаях представлены характеристики фильтров 2-10-го порядков. Включены также характеристики фильтров Бесселя 2-6-го порядков.

На основе расчетных формул можно сконсзруировать следующие типы фильтров:

1. Фильтры Баетерворта, Чебышева, инверсные Чебышева и эллиптические нижних и верхних частот с порядком, лежащим в пределах от 2 до 10, и полосно-пропус-кающие и полосно-заграждающие типы фильтров 2, 4, 6, ..., 20-го порядков.

2. Фазосдвигающие или всепропускаю-щие фильтры 2-го порядка.

3. Фильтры Бесселя или фильтры с постоянным Бременем замедления 2-6-го порядков.

4. Всепропускающие с постоянным временем замедления фильтры 2-6-го порядков.

Для фильтров Чебышева и эллиптических выбрана неравномерность передачи

Б полосе пропускания 0,1; 0,5; 1; 2 и 3 дБ, а для фильтров инверсных Чебышева и эллиптических табулировано минимальное затухание в полосе задержания от 30 до-100 дБ с шагом 5 дБ.

Для каждого типа фильтра приведены.-наиболее широко используемые структуры: фильтров различной сложности, от схем на источниках напряжения, управляемых напряжением на одном операционном усилителе (ОУ), до биквадратных схем иа трех ОУ.

Каждый тип фильтра рассмотрен в отдельной главе, а в конце главы приведено-краткое изложение каждой методики расчета и даны практические рекомендации. Для большинства типов фильтров подробно-рассмотрены численные примеры и даны амплитудно-частотные характеристики реальных фильтров. Каждый тип снабжен, методиками настройки, а ширина переходных областей либо табулирована (для эллиптических фильтров), либо задана формулами.

Одной из особенностей книги являете» то, что материал каждой главы не зависит от других, а краткое изложение расчета в конце самой главы не связано с остальной ее частью. Следовательно, можно использовать эти рекомендации для расчета практических фильтров без чтения или-понимания материала самих глав.

При подготовке этой книги бесценное-содействие оказали многие специалисты. В частности, хочется особенно поблагодарить миссис Мари Джайне (Marie Jines) и миссис Норму Даффи (Norma Duffy) соответственно за высококвалифицированную перепечатку рукописи и вычерчивание-иллюстраций.

Авторы

ГЛАВА ПЕРВАЯ ВВЕДЕНИЕ

1.1. ЧАСТОТНО-ИЗБИРАТЕЛЬНЫЕ ФИЛЬТРЫ

В большинстве случаев электрический фильтр представляет собой частотно-избирательное устройство. Следовательно, он пропускает сигналы определенных частот и задерживает или ослабляет сигналы других частот. Наиболее общими типами частхэтно-избирательных фильтров являются фильтры нижних частот (которые пропускают низкие частоты и задерживают высокие частоты), фильтры верхних частот (которые пропускают высокие частоты и задерживают низкие частоты), полосно-пропускаю-щие фильтры (которые пропускают полосу частот и задерживают те частоты, которые расположены выше и ниже этой полосы) и полосно-заграждающие фильтры (которые задерживают полосу частот и пропускают частоты, расположенные выше и ниже этой полосы).

Более точно характеристику частотно-избирательного фильтра можно описать, рассмотрев его передаточную функцию

H{s) = V2(s)/V,(s). (1.1)

Величины Vi и V2 представляют собой соответственно входное и выходное напряжения, как показано на общем изображе- НИИ фильтра на рис. 1.1. Для установившейся частоты s=/co (/=V - 1) передаточную функцию можно переписать в виде

Я(/со) = 1Я(/со)1е>(1.2)

где \Н(ja) \ - модуль передаточной функции или амплитудно-частотная характеристика; ff(a)-фаао-частотная характеристика, а частота ю (рад/с) связана с частотой f (Гц) соотношением И)=2я/.

Диапазоны или полосы частот, в которых сигналы проходят, называются полосами пропускания и в них значение ампли-

тудно-частотной характеристики Я(/сй)1 относительно велико, а в идеальном случае постоянно. Диапазоны частот, в которых сигналы подавляются, образуют полосы задерживания и в них значение амплитудно-частотной характеристики относительно мало, а в идеальном случае равно нулю.-В качестве примера на рис. 1.2 штриховой линией показана амплитудно-частотная характеристика идеального фильтра нижних частот с единственной полосой пропускания 0<co<(Dc и полосой задерживания сй> >fuc. Частота сОс между двумя этими полосами определяется как частота среза.

На практике невозможно реализовать эту идеальную характеристику, поскольку требуется сформировать очень узкую переходную область. Следовательно, основная проблема при конструировании фильтра заключается в приближении реализованной в лаборатории реальной характеристики с заданной степенью точности к идеальной. Вариант такой реальной характеристики показан сплошной линией на рис. 1.2.

В практическом случае полосы пропускания и задерживания четко не разграничены и должны быть формально определены. Исходя из нашего определения в качестве полосы пропускания выбирается дна--пазон частот, где значение амплитудно-частотной характеристики превышает, некоторое заранее выбранное число, обозначенное Al на рис. 1.2, а полосу задерживания образует диапазон частот, в котором ам; плитудно-частотная характеристика меньше

Wjw)\

Идеальная

Реальная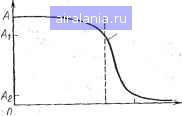

Рис. 1,1.

Изображение фильтра

электрического

Рис. 1.2. Идеальная и реальная амплитудно-частотные характеристики фильтра нижних частот.