в. Настройка осуществляется следующим образом: изменяя сопротивления Rt или Ri, Rs и Rz, получают соответственно требуемые К, fc и вид характеристики в полосе пропускания (см. § 4.6). При необходимости эти этапы можно повторить. Сопротивление Rs можно выбрать произвольно для сохранения небольшого разброса значений сопротивлений.

г. Этот фильтр можно использовать для значений добротности Q<100.

Биквадратный фильтр верхних частот был рассмотрен в § 4.4.

4.11. РАСЧЕТ ЭЛЛИПТИЧЕСКОГО ФИЛЬТРА ВЕРХНИХ ЧАСТОТ НА ИНУН

Для расчета эллиптического или инверсного Чебышева фильтра верхних частот второго порядка или звена второго порядка фильтра более высокого порядка, обладающего заданной частотой среза fc (Гц), или (йс=2я/с (рад/с), коэффициентом усиления К, минимальным затуханием в полосе задерживания (MSL), а для эллиптического фильтра и неравномерностью передачи в полосе пропускания (PRW), необходимо выполнить следующие шаги.

1. Найти нормированные значения коэффициентов нижних частот Л, В и С из соответствующей таблицы в приложении Б или В.

2. Выбрать номинальное значение емкости С, (предпочтительно близкое к значению 10/fc мкФ) и вычислить сопротивления

Ri=AB/KC<i)cCi; ?2=C/BwcC2. Rs=KCRi/A; Ri=KR,/ii; R(.=ixR2l(ix-\); R7=iiR2,

где Cz, Rs и fi>l имеют произвольные

значения.

Если К и добротность Q= VC/B имеют небольшие значения, а именно не более 10, то приемлемое значение этих произвольных параметров равно

С2=Сг, 7?5=l/o)cCi,

а ц=2 (в этом случае Re=R7). Если Q и/или К имеют большое значение, например выше 10, то Сг, Rs к ц должны выбираться таким образом, чтобы сохранить небольшой разброс значений сопротивлений.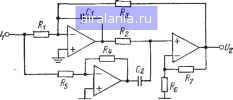

Рис. 4.12. Схема эллиптического фильтра верхних частот на ИНУН.

3. Выбрать номинальные значения сопротивлений, наиболее близкие к вычисленным значениям, и реализовать фильтр ил» его звенья в соответствии со схемой, показанной на рис 4.12.

4. Если требуется р;=1, то сопротивление Re заменяется на разомкнутую, а сопротивление Rt на короткозамкнутую цепи,, а значения других сопротивлений определяются как на шаге 2. В этом случае получаем схему на повторителе напряжения (см. рис. 3.6).

Комментарии

а. Комментарии пп. а, б и е для фильтра с мое в § 4.8 используются непосредственно, за исключением того, что в п. б сопротивление Req каждого ОУ определяется значением сопротивления Ru R2-или Rs, подключенного к его инвертирующему входному контакту.

б. Эта схема может использоваться-как для высоких, так и для низких значений добротности Q с помощью выбора произвольных параметров из шага 2 таким образом, чтобы сохранялся относительно небольшой разброс значений сопротивлений. Для небольших коэффициентов усиления Q<100.

в. Настройка осуществляется следующим образом: изменяя отношение Ri/Rs, устанавливают максимальное подавление на частоте fz, как показано на рис. 4.7.

Коэффициент усиления ИНУН

lx=l+R7/Re

регулируется с помощью изменения отношения Ri/Re для установки подъема пг> частоте fm- Наконец, для получения значения Km изменяют сопротивление Rs- Эти этапы можно повторять до тех пор, пока звено не будет настроено.

г. Эта схема обеспечивает инвертирующий коэффициент усиления K=\JtRi/R5-

Эллиптический фильтр верхних частот на ИНУН был рассмотрен в § 4.5.

4.12. РАСЧЕТ ЭЛЛИПТИЧЕСКОГО ФИЛЬТРА ВЕРХНИХ ЧАСТОТ НА ТРЕХ КОНДЕНСАТОРАХ

Для расчета эллиптического или инверсного Чебышева фильтра верхних частот второго порядка или звена второго-порядка фильтра более высокого порядка, обладающего заданной частотой среза f (Гц), или wc==2jtfc (рад/с), коэффициентом усиления К, минимальным затуханием в полосе задерживания (MSL), а для эллиптического фильтра и неравномерностью передачи в полосе пропускания (PRW), необходимо выполнить следующие шаги.

1. Найти нормированные значения коэффициентов нижних частот Л, В и С иэ соответствующей таблицы в приложении Б или В.

2. Выбрать номинальное значение емкости Cl (предпочтительно близкие к зна-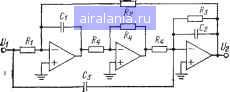

Рис. 4.13. Схема эллиптического фильтра верхних частот на трех конденсаторах.

чению 10/fc мкФ) и вычислить значения элементов

Сз=КС2, RiA/RiOihCtCs;

RKCRi/A; RsC/BwcCz,

где Сг и Ri имеют произвольные значения. Если значение добротности Q=VC/B невелико, то значение емкости Сг можно выбрать близким к значению Ci, а если Q велико, то значение Сг берется большим, чем Ci. В любом случае сопротивление ,4 необходимо выбирать таким образом, чтобы минимизировать разброс значений сопротивлений.

3. Выбрать номинальные значения сопротивлений и емкостей, наиболее близкие к вычисленным значениям, и реализовать фильтр или его звенья в соответствии со схемой, показанной на рис. 4.13.

Комментарии

а. Комментарии пп. а, б и е для фильтра с мое в § 4.8 используются непосредственно, за исключением того, что в п б сопротивление Req каждого ОУ определяется значением сопротивления Ri или Ri, подключенйого к его инвертирующему входному контакту.

б. Эта схема может использоваться как для высоких, так и для низких значений добротности iQ, верхний предел которой приблизительно равен 100.

в. Настройка осуществляется следующим образом: сначала, изменяя сопротивление Ru устанавливают максимальное подавление на частоте fz (см. рис. 4.7), затем, изменяя сопротивление R, размещают подъем амплитудно-частотной характеристики на частоте fm и, наконец, изменяя сопротивление Rs, получают требуемое значение Km- Для низкодобротных звеньев последние два этапа, возможно, необходимо будет повторить.

г. Эта схема обеспечивает инвертирующий коэффициент усиления К=Сз/С2.

Схема на трех конденсаторах была рассмотрена в § 4.5.

4.13. РАСЧЕТ БИКВАДРАТНОГО ЭЛЛИПТИЧЕСКОГО ФИЛЬТРА ВЕРХНИХ ЧАСТОТ

Для расчета эллиптического или инверсного Чебышева фильтра верхних частот второго порядка или звена второго порядка фильтра более высокого порядка,

UiO-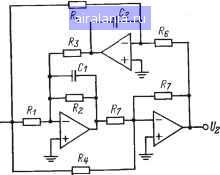

Рис. 4.14. Схема биквадратного эллиптического фильтра верх:шх частот.

обладающего заданной частотой среза fc (Гц), или a)c=2jtfc (рад/с), коэффициентом усиления К, минимальным затуханием в полосе задерживания (MSL), а для эллиптического фильтра и неравномерностью передачи в полосе пропускания (PRW), необходимо выполнить следующие шаги.

1. Найти нормированные значения коэффициентов нижних частот Л, В и С из соответствующей таблицы в приложении Б или В.

2. Выбрать номинальное значение емкости Ci (предпочтительно близкое к значению 10/fc мкФ) и вычислить значения элементов

Ri=CIKBacd; RKRi; /?з = Кс/«сС,; R = R,/K; Rs = А/К VCv>cC2; Re = C,R,/C,.

Значения Сг и Ri выбираются произвольно в зависимости от коэффициента усиления К и добротности Q= VC/B для минимизации разброса значений сопротивлений. Для небольших значений К к Q их приемлемые значения составляют: С2=

=Ci и i?7=l/«cCl.

3. Выбрать номинальные значения сопротивлений и емкостей как можно ближе к вычисленным значениям и реализовать фильтр или его звенья в соответствии со схемой, показанной на рис. 4.14.

Комментарии

а. Комментарии пп. а, б и е для фильтра с МОС в § 4.8 используются непосредственно, за исключением того, что в п. б сопротивление Req каждого ОУ определяется значением сопротивления Ri, Re или /?7. подключенного к его инвертирующему входу.

б. Эта схема может использоваться как для высоких, так и для низких значений добротности Q, верхний предел которой приблизительно равен 100.

в. Настройка осуществляется следующим образом: изменяя сопротивления Ri,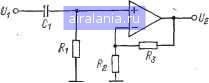

Рис. 4.15. Схема фильтра верхних частот первого порядка.

Rs, R2 и Ri, устанавливают соответственно максимальное подавление на частоте fz, частоту среза, добротность Q и коэффициент усиления.

г. Эта схема обеспечивает инвертирующий коэффициент усиления, равный 2/?!.

Биквадратный эллиптический фильтр был рассмотрен в § 4.5.

4.14. РАСЧЕТ ФИЛЬТРА ВЕРХНИХ ЧАСТОТ НЕЧЕТНОГО ПОРЯДКА

Для расчета звена первого порядка фильтра верхних частот более высокого нечетного порядка заданного типа (например, фильтра Баттерворта, Чебышева, инверсного Чебышева или эллиптического), обладающего заданной частотой среза fc (Гц), или сйс=2зг/с (рад/с), коэффициентом усиления звена К, минимальным затуханием в полосе задерживания (MSL) и, если используется, неравномерностью передачи в полосе пропускания (PRW), необходимо выполнить следующие шагн.

1. Найти нормированный ко.уффициент нижних частот С для звена первого порядка из соответствующей таблицы в приложении А, Б или В.

2. Выбрать номинальное значение емкости Cl (предпочтительно близкое к значению 10/fc мкФ).

За. Если Я>1, вычислить значения сопротивлений

R, = Clti)cCu R2=KRi/{K-~l); /?3=W. и реализовать этот фильтр в соответстнии со схемой, показанной на рис. 4.15.

б. Если К=1, использовать сопротивление 1 из пункта За и заменить сопротивление Rs разомкнутой, а сопротивление Ra короткозамкнутой цепями. В результате получим схему на повторителе напряжения.

4. Звенья второго порядка этого фильтра нечетного порядка можно реализовать с помощью рассмотренных в предыдущих параграфах Мч.».тодов на основе каскадного их соединения с звеном первого порядка.

Комментарии

а. Комментарии пп. а и б для фильтра с МОС в § 4.8 используются непосредственно, за исключением того, что в п. б

Re-Rl.

б. Значения сопротивлений R2 и Rs выбираются таким образом, чтобы минимизировать смешение ОУ по постоянному току. Можно использовать другие их значения при условии, что сохраняется их отношение, и в этом случае

К=1+(Лз/«2).

В. Коэффициент усиления К>1 можно настроить, используя вместо резисторов R2 и Rs потенциометр, центральный отвод которого подключен к инвертирующему входу ОУ. Требуемая частота среза получается при изменении сопротивления Ri. Характеристика должна иметь вид, показанный на рпс. 4,6,6.

Фильтр верхних частот первого порядка был рассмотрен в § 4.7.

ГЛАВА ПЯТАЯ ПОЛОСНО-ПРОПУСКАЮЩИЕ ФИЛЬТРЫ

5.1. ОБЩИЙ СЛУЧАЙ

Полосно-пропускаюищй фильтр представляет собой устройство, которое пропускает сигналы в диапазоне частот с шириной полосы BW, расположенной приблизительно вокруг центральной частоты а>о (рад/с), или fo=aio/2jt (Гц). На рис. 5.1 изображены идеальная и реальная амплитудно-частотные характеристики. В реальной характеристике частоты (Oi и (0(7 представляют собой нижнюю и верхнюю частоты среза и определяют полосу пропускания (Oiw col и ее ширину BW=(uc7-(Вг,-

В полосе пропускания амплитудно-частотная характеристика никогда не превышает некоторого определенного значения, например Ai на рис. 5.1. Существует также две полосы задерживания OoWi и (Bcos, где значение амплитудно-частотной

характеристики никогда не превышает за-)анее выбранного значения, скажем, Лг. Диапазоны частот между полосами задерживания и полосой пропускания, а именно (Bi<(o<(Or, и (Вс7<(о<(02, образуют соответственно нижнюю и верхнюю переходные области, в которых характеристика является монотонной.

Отношение Q={flo/BW характеризует качество самого фильтра и является мерой его избирательности. Высокому значению Q соответствует относительно узкая, а низкому значению Q - относительно широкая ширина полосы пропускания. Коэффициент усиления фильтра К определяется как значение его амплитудно-частотной характеристики на центральной частоте; таким образом, /С==!Я(/(Оо) .

Передаточные функции полосно-пропус-кающих фильтров можно получить из нор-