ввеиа второго порядка полосио-пропускаю-щего фильтра более высокого порядка фильтров Баттерворта, Чебышева, инверсного Чебышева или эллиптического. В этом случае из (5.4) находим p=KC/Q, Р= =C/Q и у=1. Наконец, уравнение (5.32) описывает передаточную функцию двух по-досно-пропускающих звеньев, получаемых из соответствующего фильтра Баттерворта или Чебышева нижних частот второго порядка. В этом случае из (5.7) и (5) находим для двух звеньев p=KiVC/Q, .=D/E. y=D и р= KVC/Q, P=l/Z)£. V=I/jD2.

Звенья второго порядка эллиптического или инверсного Чебышева полосно-пропускающего фильтра, соответствующие звеньям нижних частот второго порядка, .имеют передаточные функции вида (5.15):

J (+co Т/, s + m,s + -iw,

Каждому звеиу иижиих частот соот-ветствуют два полосио-пропускающих звена <; функциями вида (5.36). Эти функции -описываются уравнениями (5.12) и (5.13), из которых следует, что р= Кл Vc/A , a=i4i, =D/E, y=D в первом случае и .p=KVC/A, а=1/л1, Р= ! )£, у= -l/D во втором случае. Одна нз них соответствует звену нижних частот, амплитудно-частотная характеристика которого показана на рис. 3. 1,с или б. Другая соответствует звену верхних частот с амплитудно-частотной характеристикой, изображенной на рис. 4.7,а или б. Функция (5.12) является функцией звена нижних частот при Ai>D и функцией звеиа верхних частот в остальных случаях. Подъем амплитудно-частотной характеристики на ;рис. 3.11,а и 4.7,а

2р /- (a-Y)2-fa --Г Г 4Y-P

(5.37)

а расположен на частоте

На постоянном токе значение амплитудно-частотной характеристики равно ра/у и fi= fo во всех четырех слу-

чаях (см. рис. 3.11 и 4.7).

Методики настройки отдельных полосио-пропускающих фильтров будут приведены далее.

5.9. ОБЩИЕ СВЕДЕНИЯ ПО РАСЧЕТУ И ПОСТРОЕНИЮ ПОЛОСНО-ПРОПУСКАЮЩЕГО ФИЛЬТРА

Далее приведены схемы и сокращенные методики получения полосио-пропускающих фильтров второго порядка и звеньев второго порядка фильтров Баттерворта, Чебышева, инверсных Чебышева и эллип-

тических высокого порядка. Для получения полосно-пропускающих фильтров будут использоваться приведенные в приложениях А, Б и В исходные данные соответствующих фильтров нижних частот.

Состоящие из одного звена второго порядка фильтры можно реализовать, используя приведенные в § 5.10. 5.11 или 5.12 схемы с МОС, на ИНУН и биквадратные схемы.

Для фильтров высокого порядка число звеньев второго порядка равно порядку соответствующего фильтра нижних частот. Полосно-пропускающее звеио, соответствующее звену нижних частот первого порядка, можно реализовать на основе схем с МОС, на ИНУН и биквадратных схем. Каждому звену нижних частот второго порядка будут соответствовать два полосио-пропускающих звена второго порядка. Для полосно-пропускающих фильтров Баттерворта или Чебышева это могут быть также схемы с МОС, на ИНУН и биквадратные схемы, а для инверсных Чебышева и эллиптических полосно-пропускающих фильтров реализация должна осуществляться как изложено в § 5.13, 5.14 или 5.15.

В качестве примера предположим, что требуется получить полосно-пропускающий инверсный фильтр Чебышева шестого порядка с К=8, f0=1000 Гц, (2=5 и MLS= =40 дБ. Из приложения Б для N=3 находим звено нижних частот первого порядка с С= 1,060226 и звено нижних частот второго порядка с Л=12,075684, В>= =0,969938 и С= 1,028354. Поскольку имеется три полосио-пропускающих звена второго порядка, то выберем коэффициент усиления каждого звена равным 2. Функция звеиа, соответствующая сомножителю функции нижних частот первого порядка, определяется уравнением (5.4), для которого

КСч,„ 2(1.060226) (2000п) „

-- = --~-- = 2664, 639;

Ccuo/,Q= 1332,319; 0==3978. iqb Эту функцию можно реализовать с помощью схемы с МОС, на ИНУН или биквадратной схемы.

Функции двух звеньев, соответствующих сомножителю функции нижних частот второго порядка, описываются уравнениями (5.12) и (5.13), где Ki=Kx=2. Из (5.14), 15.10) и (5.9) получаем л1=1,977, Ih= = 1,093 и £=10,351. Поскольку Ai>D\ то (5.12) соответствует функции нижних частот, а (5.13)-функции верхних частот. Эти два звена можно реализовать иа основе схем, приведенных в § 3.3, 3.4 или 3.5.

5.10. РАСЧЕТ ПОЛОСНО-ПРОПУСКАЮЩЕГО ФИЛЬТРА С МНОГОПЕТЛЕВОИ ОБРАТНОЙ СВЯЗЬЮ

Для расчета а) полосно-пропускающего фильтра второго порядка, б) звена второго порядка полосно-пропускающего филь-

гра Баттерворта, Чебышева, инверсного Чебышева или эллиптического более высокого порядка, соответствующего звену нижних частот первого порядка или в1 звеиа второго порядка полосно-пропускающего фильтра Баттерворта или Чебышева высокого порядка, соответствующего звену нижних частот второго порядка, обладающих заданной центральной частотой fo (Гц), или cuo=23Tfo (рад/с), коэффициентом усиления звена К и добротностью Q, необходимо выполнить следующие шаги.

1. Для расчета п. б найти нормированный коэффициент С звена нижних частот первого порядка, а для расчета п. в- нормированные коэффициенты В-С звена нижних частот второго порядка из соответствующей таблицы в приложении А, Б и В.

2. Выбрать номинальное значение емкости Cl (предпочтительно близкое к значению 10/fc мкФ) и номинальное значение емкости Сг, удовлетворяющее условию

С2>С,(рР-v)/»Y. и вычислить сопротивления /?1==1/р(ВоСг,

[Ci(y-pP) + yC2]o

Для п. а получас»,

P=jK/Q; р=1. Q: Y=l;

для п. б

p=KC/Q; fi=C/Q; у=1:

для фильтров в п. в соотУ1Этствуют два звена, первое имеет

g = KVc/Q; D/E; = D\ а второе

р = ДГС/0; p=l/Z)£; y =l/D

С -j- 40= + V{C+4Q)-{2BQy;

Z) = -

ВЕ Q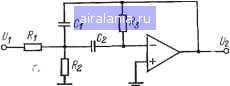

Рис. 5.11. Схема полосно-нропускающего фильтра с МОС.

3. Выбрать номинальные значения сопротивлений, наиболее близкие к вычисленным значениям, и реализовать фильтр» или его звенья в соответствии со схемой,, показанной иа рис. 5.11 (см. также общие-сведения по различным фильтровым звеньям, приведенные в § 5.9).

Комжнтарии

а. Для обеспечения лучших рабочих характеристик номинальные значения элементов должны выбираться наиболее близкими к выбранным и вычисленным значениям. Фильтры высокого порядка требуют применения более точных значений элементов, чем фильтры сравнительно низкого, порядка. Рабочая характеристика фильтра-не изменится, если значения всех сопротивлений умножить, а емкостей поделить, на общий множитель.

б. Входное полное сопротивление оу должно быть по крайней мере lOReg, где

Reg=R3

Коэффициент усиления ОУ с разомкнутой обратной связью должен по крайней мере в 50 раз превышать значение амплитудно-частотной характеристики фильтра, или звена на частоте fa - наибольшей требуемой частоте в полосе пропускания, а его скорость нарастания (В/мкс) должна bi 0,5(Ва-10~ раз превосходить максимальный размах выходного напряжения.

в. Инвертирующий коэффициент усиг ления

K=R,Cs./Ri{Ci+C2). Следовательно, коэффициент усилений можно настроить, изменяя сопротивление-Ri. Для получения требуемой добротности. Q изменяют сопротивление Ri, и, изменяя, одновременно сопротивления Rz и R3 в одинаковом процентном отношении, можно, не влияя на добротность Q, установить центральную частоту. При необходимости эти. этапы можно повторить (см. также § 5.8).

г. Эту схему можно использовать только для фильтровых звеньев с коэффициентом усиления /С=р/р и добротностью Q=

V-i/ ие более 10. Коэффициент усиления может быть и больше для небольших, значений Q, при вьшолиеиии ограничения-KQ=m и Q=10.

д. Порядок фильтра, требуемый для. обеспечения заданной ширины верхней и. нижней переходных областей, или, наоборот, ширину переходных областей, соответствующих заданному порядку, можно» иайти по методике из § 5.3.

Полосно-нропускающий фильтр с МОС был рассмотрен в § 5.4.

5.11. РАСЧЕТ ПОЛОСНО-ПРОПУСКАЮЩЕГО ФИЛЬТРА НА ИНУН

Для расчета а) полосно-пропускающего-фильтра второго порядка, б) звена второго, порядка полосно-пропускающего фильтра Баттерворта, Чебышева, инверсного Чебы-

41, Pi

Ь-1 г

R 5

Фис. 5.12. Схема полосио-пропускающего фильтра на ИНУН.

шева или эллиптического более высокого порядка, соответствующего звеиу иижиих частот первого порядка или в) звеиа второго порядка полосно-пропускающего фильтра Баттерворта или Чебыщева высо-кого порядка, обладающих заданной центральной частотой fo (Гц), или й)о=2я/о (рад/с), коэффициентом усиления звеиа К я добротностью Q, необходимо выполнить следующие шаги.

1. Для расчета п. б найти нормированный коэффициент С звена нижних частот первого порядка, а для расчета п. в - нор-•мированные коэффициенты В и С звена нижних частот второго порядка из соответствующей таблицы в приложении А, Б или В.

2. Выбрать номинальное значение емкости Ct (предпочтительно близкое к значению W/fo мкФ) и вычислить сопротивления

i?i=2/pcuoCi;

2

[-P+>(P-P) + 8y] со а

р J / L L.N.

/?4=/?5=2/?з.

(Более общий расчет для случая R,ФRi приведен в § 5.5.)

Для п. а получаем

Р=т; P=i/Q;

для п. б

p=KCIQ; d, = CfQ; у=1;

для фильтров в п. в соответствуют два звена, первое имеет

P = kV"C/Q; = D/E; Y = -D а второе

p = iClC/Q; p = i/D£; Yli?"-

где

-iff + /(fr-

3. Выбрать номинальные значения сопротивлений как можно ближе к вычисленным значениям и реализовать фильтр или его звенья в соответствии со схемой, показанной на рис. 5.12. (См. также приведенные в § 5.9 общие сведения по различным фильтровым звеньям.)

Комментарии

а. Комментарии пп. а, б, г и д для фильтра с МОС в § 5.10 используются непосредственно.

б. Значения сопротивлений Rt. и Ri выбираются таким образом, чтобы минимизировать смещение ОУ по постоянному току. Можно использовать другие значения при условии, что их отношение Rs/Rtl (или l-H?5/Ri=M, которое применяется прч более общем расчете в § 5.5).

в. Неинвертирующий коэффициент усиления этого фильтра можно настроить путем изменения сопротивления Ri (или при более общем расчете в § 5.5 изменением отношения Ri/Ri.). Центральная частота устанавливается изменением сопротивления Rs, добротность Q - сопротивлений Rz и Rs- Эти этапы влияют друг на друга, однако их можно повторять. (См. в § 5.8 другие особенности настройки.)

Полосно-пропускающий фильтр на ИНУН был рассмотрен в § 5.5.

5.12. РАСЧЕТ БИКВАДРАТНОГО ПОЛОСНО-ПРОПУСКАЮЩЕГО ФИЛЬТРА

Для расчета а) полосно-пропускающего фильтра второго порядка, б) звена второго порядка полосио-пропускающего фильтра Баттерворта, Чебышева, инверсного Чебышева или эллиптического более высокого порядка, соответствующего звену нижних частот первого порядка или в) звена второго порядка полосно-пропускающего фильтра Баттерворта или Чебышева высокого порядка, соответствующего звеиу нижних частот второго порядка, обладающих заданной центральной частотой /о (Гц), или (Во=2зт/о (рад/с), коэффициентом усиления звена К и добротностью Q, необходимо выполнить следующие шаги.

1. Для расчета п. б найти нормированный коэффициент С звеиа нижних частот первого порядка, а для расчета п. в нормированные коэффициенты В и С звена нижних частот второго порядка из соответствующей таблицы в приложении А, Б или В.

2. Выбрать номинальное значение емкости d (предпочтительно близкое к значению 10 о мкФ) и вычислить сопротивления

Ri=l/paoCi;

/?2 = - = -7-/?,;

рсйсС, р

Rsl/yaoCiRi,