Z Л. с к

Ra = -

Для второго звена:

Kv>,Ci V С

-Ri,

Rs=-

A Ri

/?5 =

с К

Ax ./

R<

В обоих случаях Сг и R-i имеют произвольные значения, а Ai, Е и D определяются из следующих соотношений:

l/(f)-

В зависимости от коэффищ!ента усиления К и добротности Q=E значения Cj и R-! выбираются таким образом, чтобы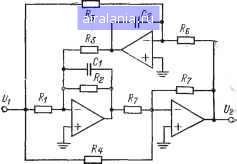

Рис. 5.16. Схема биквадратного эллиптического полосно-пропускающего фильтра..

минимизировать разброс значений сопротивлений.

3. Выбрать номинальные значения сопротивлений и емкостей как можно ближе к вычисленным значениям и реализовать фильтровые звенья в соответствии со схемой, показанной на рис. 5.16.

Комжнтарии

а. Комментарии пп. а, б и д для фильтра с МОС в § 5.10 используются непосредственно, за исключением того, что в п. б сопротивление Reg каждого ОУ определяется значением сопротивления

Re или i?7, соединенного с его инвертирующим входом.

б. Эта схема может использоваться как для высоких, так и для низких значений добротности Q-E, верхний предел которой равен 100.

в. Настройка осуществляется следующим образом: изменяя сопротивления Rt,. Rs, R2, Ri или Rs, устанавливают соответственно максимальное подавление на частоте /г, центральную частоту, добротность Q и коэффициент усиления.

г. Эта схема обеспечивает инвертирующий коэффициент усиления -/С(Л>0),. который пропорционален Rz/Ri.

Биквадратная эллиптическая схема была рассмотрена в § 5.7.

ГЛАВА ШЕСТАЯ ПОЛОСНО-ЗАГРАЖДАЮЩИЕ ФИЛЬТРЫ

6.1. ОБЩИЙ СЛУЧАЙ

Полосно-заграокдающий фильтр (называется также полосно-задерживающим или полосно-исключающим, или V-образным) представляет собой устройство, которое подавляет сигналы в единственной полосе частот и пропускает сигналы со всеми другими частотами. Эта полоса подавления характеризуется шириной BW и расположена приблизительно вокруг центральной частоты (Оо (рад/с), или fo==coo/2n

(Гц). Идеальная и реальная амплитудно-частотные характеристики полосно-заграж-дающего фильтра изображены на рис. 6. к Для реальной амплитудно-частотной характеристики частоты COl и <Bi7 представляют собой нижнюю и верхнюю частоты среза, определяющие полосу подавления Оьсоми и ее ширину BW=o3i7-соь. Все эти параметры имеют свои аналоги в рассмотренном в гл 5 полосно-пропу-скающем фильтре.

, Что же касается реальной характеристи-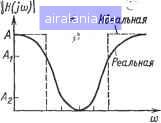

Ui w-i Шо шг шц

Рис. 6.1. Идеальная и реальная амплитуд-sjo-4acTOTHbie характеристики полосно-за-граждающего фильтра.

«и, показанной на рис. 6.1, то в полосе •лодавлеиия она никогда не превосходит не-«оторого заранее выбранного значения, (например Аг. Существуют также две полосы пропускания 0©<»i, и шмр, где значение амплитудно-частотной характеристики всегда больше Аи Определим полосу задерживания как диапазон частот <01<шо)2, где значение амплитудно-частотной характеристики никогда не превосходит выбранного числа МкАи Тогда диапазоны частот o>i.<(o<toi и со2<со< <toi7 называются соответственно нижней т верхней переходными областями и в них характеристика монотонна.

Соотношение Q=coo/BW, как и в по-лосно-пропускающем аналоге, характеризует добротность этого фильтра и определяет его избирательность. Высокому значению Q соответствует относительно узкая, а низкому значению Q относительно широкая полоса частот. Коэффициент усиления К фильтра представляет собой значение его амплитудно-частотной характеристики, снятую при постоянном токе, т. е. =Я(/0).

Полосно-заграждающие передаточные функции можно получить из нормированных функций нижних частот переменной ,S с помощью преобразования типа [16].

5=. . (6.1)

s=-bw„= Q(s + W)

Следовательно, подобно полосно-пропу-скающему фильтру полосно-заграждающий фильтр всегда имеет четный порядок я=2, 4, 6 ... Результирующий полосно-заграждающий фильтр в зависимости от соответствующей ему функции нижних частот имеет характеристику фильтра Баттерворта, Чебышева, инверсного Чебышева или эллиптического. Амплитудно-частотная характеристика по-лосно-заграждающего фильтра Баттерворта изменяется монотонно по .любую сторону от его частоты подавления или центральной частоты, как показано на рис. 6.1. Полосно-заграждающий фильтр Чебышева обладает пульсациями в полосе пропускания, а полосно-заграждающий инверсный . фильтр Чебышева - в полосе задерживания. Для полосно-заграждающего эллипти-

Рис 6.2. Амплитудно-частотная характеристика реального полосно-заграждающего фильтра Чебышева четвертого порядка.

Рис. 6.3. Амплитудно-частотная характеристика эллиптического полосно-заграждающего фильтра шестого "порядка.

ческого фильтра характерны пульсации как в полосе пропускания, так и в полосе задерживания. В каждом случае центральная частота и частоты среза связаны следующим соотношением: сйо= . Частоты полосы пропускания

Частоты полосы задерживания

(6.2)

4Q/Q=

(6.3)

где частота fis представляет собой начало полосы задерживания соответствующего

фильтра нижних частот. Другими словами,

Q»=1+TW, (6.4)

где TW - нормированная ширина переходной области соответствующего фильтра нижних частот, определенная ранее уравнениями (2.16), (2.17) и (3.7) при tdc=l Лля характеристик фильтров Баттерворта, Чебышева и инверсных Чебышева, а для арактеристик эллиптических фильтров ее значение указано в таблице приложения В. Можно отметить также, что (оо= .со,.

Примеры амплитудно-частотных характеристик полосно-заграждающих фильтров наказаны на рис. 6.2 и 6.3. На рис. 6.2 приведена характеристика полосно-заграждаю-щего фильтра Чебышева четвертого порядка с неравномерностью передачи 1 дБ, /о=60 Гц и Q=10.

Характеристика эллиптическая полос-яо-заграждающего фильтра шестого порядка с неравномерностью передачи в полосе пропускания 3 дБ, минимальным затуханием в полосе задерживания 40 дБ, fo= =60 Гц и Q=5 изображена иа рис. 6.3.

6.2. ПЕРЕДАТОЧНЫЕ ФУНКЦИИ

Как и в рассмотренных в гл. 5 передаточных функциях полосно-пропускающих фильтров, полосно-заграждающие функции получаются из соответствующих функций нижних частот. Функция полосно-заграж-дающего фильтра задается в виде произведения сомножителей, каждый из которых получается из сомножителя функции нижних частот. Для сомножителя функции нижних частот первого порядка

КС S + C

(6.5)

соответствующий сомножитель полосно-за-граждающей функции представляет собой оуикцию второго порядка

Vi K[±w}

V, s2+(co„/CQ)6+to„2

(6.6)

где С - нормированный коэффициент соответствующего звена нижних частот первого порядка, приведенный в приложении А для фильтров Баттерворта и Чебышева, в приложении Б для инверсного фильтра Чебышева и в приложении В для эллиптического фильтра.

Полосно-заграждающий фильтр второго порядка получается, если соответствующий фильтр нижних частот имеет первый порядок. В этом случае уравнение (6.5) при С=1 представляет собой функцию нижних частот и из (6.6) получаем следующее соотношение:

K{s+<

(6.7)

которое описывает передаточную функцию полосно-заграждающего фильтра второго

порядка. Эта функция в нашем понимании соответствует полосно-заграждающему фильтру Баттерворта или Чебышева второго порядка, хотя эти определения относятся в основном к полосно-заграждающим фильтрам более высокого порядка.

Сомножители передаточной функции полосно-заграждающего фильтра Баттерворта или Чебышева, получаемые из звеньев нижних частот второго порядка, определяются следующим образом:

/C(s4-tOo°)°

V s*+(Bco„/CQ)5-f

"* +(2-bl/CQ2)co„2s2+(Bo„VCQ)s-fco„*

где В и С - соответствующие коэффициенты нижних частот из приложения А. В (6.6) К определяет коэффициент усиления звена, в то время как в (6.8) К задает общий коэффициент усиления двух каскад-но соединенных звеньев второго порядка, реализующих функцию четвертого порядка.

Передаточную функцию (6.8) можно записать в виде произведения двух функций второго порядка [4]:

(ti-

-; (6.9)

-,(6.10)

s=-bK/Z)i£i)s + co Z)i« 1

где fi,= -X

X]/-J[l +4CQ fK(l-.4CQ2)2-(2BQ)=]

(6.11)

L QC

(6.12)

Таким образом, передаточная функция полосно-заграждающего фильтра Баттерворта или Чебышева с порядками п=4, 6, 8 ... будет содержать описываемые соответственно уравнениями (6.9) и (6.10) сомножители для каждого звена второго порядка в соответствующем ему фильтре нижних частот. Числа Ki и Kz представляют собой коэффициенты усиления двух полосно-заграждающих звеньев и должны выбираться так, чтобы K\Ki=K.

Подводя итоги, можно сказать, что типовая передаточная функция полосно-заграждающего фильтра второго порядка или звена второго порядка полосно-заграждающего фильтра Баттерворта или Чебышева более высокого порядка имеет вид:

p(s + co/)

(6.13)