где р, р и Y получены путем сравнения (6.13) с соответствующими уравнениями (6.6), (6.7), (6.9) и (6.10). В обоих уравнениях (6.9) и (6.10) параметр Ei определяет добротность Q каждого звена и, подобно рассмотренным ранее фильтрам, для реализации высоких значеиий Q обычно требуются более качественные схемы.

Для эллиптических или инверсных Чебышева полосно-заграждяющих фильтров передаточную функцию также можно представить в виде произведения функций второго порядка. Если соответствующий фильтр нижних частот имеет нечетный порядок, то сомножитель полосно-заграждаю-щей функции, получаемый из звена нижних частот первого порядка, описывается уравнением (6.6), которое, как уже было отмечено, является частным случаем уравнения (6.13). Эти два сомножителя, получаемые из передаточной функции каждого звена нижних частот, определяются следующим образом:

/Г,(£М-Л«оЗ

+ (i>ifo„/£,)s + Z)i=co„

-; (6.14)

s= + (co„/A£,)s-)-co„VD,

i, (6.15)

где El и Dl задаются уравнениями (6.11) и (6.12) и

Коэффициенты А, В и С представляют собой нормированные коэффициенты функций нижних частот, приведенные в приложениях Б или В, а н Кг - коэффициенты усиления звеньев.

В общем случае (6.14) и (6.15) имеют

вид:

ji K£4:<)

Действительно, (6.13) получается из (6.17) при подстановке а=1. Следовательно, можно сказать, что (6.17) описывает все рассмотренные в этой главе полосно-заграждающие звенья. Следует отметить также, что (6.17) идентично (3.16), которое описывает функпии эллиптических и инверсных Чебышева фильтров нижних частот, при замене сос на too.

6.3. ШИРИНА ПЕРЕХОДНЫХ ОБЛАСТЕЙ

В § 6.1 было установлено, что полосно-заграждающий фильтр обладает двумя полосами пропускания Ошюг, и cotot;, где соь и (Ни - нижняя и верхняя частоты среза. Между полосой задерживания tui(o< £02 и каждой из этих полос пропускания расположена переходная область. Ширина нижней переходной области cotcoOi

а верхней переходной области Югюсор

Ши(ои-а)2- (6.19>

Для нахождения соответствия между/ шириной переходных областей полосно-заграждающего фильтра и соответствующего! ему фильтра нижних частот также можно использовать преобразование функции ниж них частот в полосно-заграждающую (,6..1.)> Эти соотношения имеют вид;

TW -f [Vl+4{TW+ 1>=Q= -

-(TW+ 1)/1--4Q]

2(TW-4rl)Q

(6.20>

TW - [Kl -j-4(TW+ 1)=Q= -

- (TW-f l)Kl -f 4Q=J

co„ ~ 2(TW-bl)Q

{6.21>

где TW является нормированной шириной переходной области соответствующего фильтра нижних частот. Для высокодобротныя схем хорошее приближение к (6.20) и (6.21) дает следующее соотношение:

TW, TWy TW

-[ = --2(TW-bl)Q <6.22)

которое определяет среднее значение ширины двух переходных областей. Для фильтров Баттерворта, Чебышева и инверсных Чебышева значения TW определяются! из (2.16), (2.17) и (3.7) при в>с=1, а для. эллиптических фильтров находятся из приложения В.

При заданной функции полосно-заграждающего фильтра можно использовать.. (6.20) и (6.21) для нахождения ширины, этих двух переходных областей. Кроме того, если необходимо найти фильтр наименьшего порядка с шириной переходных областей, меньшей некоторой заданной величины, то можно найти максимально допустимое значение TW и использовать его для выбора соответствующего фильтра нижних частот. Исходные данные полосно-заграждающего фильтра находятся из параметров этого фильтра нижних частот. Поскольку из (6.20) и (6.21) следует, что TWr,>TWi„ то можно выбрать fWu как максимально допустимое значение (так как TWt будет всегда меньше этого допустимого значения). Следовательно, из (6.21) соответствующая нормированная ширина TW нижних частот определяется следующим образом:

TW =

TWi,=(o,-(fli,.

(6.18)

2 {12Q (TWu) /coj - 1 - Vl 4Q} ~~ 4Q = -{[2Q(TWy)/co„]-l- . - Kr+4Q2} =

(6.23),,

Эта формула аналогична (5.21), приве--денной в § 5.3.

e.4. ПОЛОСНО-ЗАГРАЖДАЮЩИЙ ФИЛЬТР С МНОГОПЕТЛЕВОИ ОБРАТНОЙ СВЯЗЬЮ И БЕСКОНЕЧНЫМ КОЭФФИЦИЕНТОМ УСИЛЕНИЯ

Схема с многопетлевой обратной «связью (МОС) и бесконечным коэффициентом усиления [14] является одной из наиболее простых схем полосно-заграждающих фильтров второго порядка (рис. 6.4). Из анализа этой схемы следует, что она реализует уравнение (6.17) при

«o=„ = Y< = (:-b); (6.24) и условии, что

2RiRb=RiRi. (6.25)

Из второго соотношения в (6.24) очевидно, что a=Y- Следовательно, эта схема с передаточной функцией применяется исключительно для полосно-заграждающих фильтров второго порядка с передаточной функцией (6.7) или для звеньев второго порядка с передаточной функцией (6.6), которые получаются из звена нижних частот первого порядка. Для уравнения (6.6) получаем:

р=7С, а=у=1, 13=1/CQ (6.26)

я в этом мучае, решая (6.24) и (6.25), получаем

Ri = CQ/210.C,; R, = R,/ (СЩ" - 1 = 4/?,; Rs = 2R,; R, = KR, f

где Ci и Ra имеют произвольные значения, a инвертирующий коэффициент усиления равен К (.>0). Эти результаты можно использовать также и для (6.7), если С=1.

. Полосно-заграждающий фильтр с МОС имеет меньшее число элементов по сравнению с биквадратной схемой фильтра, рассмотренного в § 3.5, и обладает другими преимуществами структур фильтров с МОС нижних и верхних частот, а также и полосно-пропускающих. Инвертирующий коэффициент усиления равен Re/Rs, и эта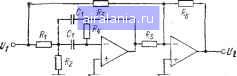

Рис. 6.4. Схема полосно-заграждающего фильтра-С МОС и бесконечным коэффициентом усиления.

Рис. 6.5. Схема полосно-заграждающего фильтра на ИНУН.

схема позволяет достигать значений добротности Q<25 [17].

Краткое изложение методики расчета приведено в § 6.8.

6.5. ПОЛОСНО-ЗАГРАЖДАЮЩИЕ ФИЛЬТРЫ НА ИНУН

Схема на ИНУН [15], изображенная на рис. 6.5, реализует передаточную функцию полосно-заграждающего фильтра второго порядка (6.17), где

aco2„ = YCo\= l/C; S (6.28)

рсо„ = 2/RCi J при условии, что

l/i?3=l ?i+l ?2. (6.29)

Из первых двух соотношений в (6.28) следует, что коэффициент усиления фильтра iK=\, а а=у. Следовательно, эта схема подобна схеме с МОС и предназначена только для фильтров второго порядка или звеньев, получаемых из звена нижних частот первого порядка.

Решая эти уравнения относительно значений сопротивлений при замене параметров р, а, р и у из (6.6), получаем

/?з=1 j

\Ri + R:

2CQco„C, 2CQ

RiRi

Ri + Ri

(6.30)

где Ci имеет произвольное значение. Определяемый уравнением (6.7) случай получается при подстановке С=1. Можно выбрать значение емкости Ci (предпочтительно близкое к 10 о мкФ), а затем определить сопротивления.

Определенным преимуществом схемы на ИНУН является минимальное число элементов и неинвертирующий коэффициент усиления. Для Q>10 получается нежелательный разброс значений элементов. Следовательно, для обеспечения хороших рабочих характеристик значение Q должно быть меньше или равно 10. Недостатком этой схемы является ограничение на коэффициент усиления, который равен 1.

6.6. НАСТРОЙКА ПОЛОСНО-ЗАГРАЖДАЮЩИХ ЗВЕНЬЕВ ВТОРОГО ПОРЯДКА

Настройка полосно-заграждающего звена второго порядка с передаточной функцией

V, - s=-f pws + Yf-

осуществляется наиболее просто, если имеется возможность наблюдать соответствующую амплитудно-частотную характеристику. Фильтр второго порядка или звено второго порядка, получаемые из звена нижних частот первого порядка, обладают амплитудно-частотной характеристикой как на рис. 6.1, за исключением того, что подавление гораздо резче. Это утверждение справедливо, поскольку в этом случае а=у=1.

Каждому звену нижних частот второго порядка будут соответствовать два полосно-заграждающих звена с передаточной функцией типа (6.31). Эти функции определяются уравнениями (6.9.) и (6.10) для фильтров Баттерворта и Чебышева и уравнениями (6.14) и (6.15) для инверсных Чебышева и эллиптических фильтров. Одно из этих двух звеньев будет звеном нижних частот (а>у) с амплитудно-частотной характеристикой, показанной на рис. 3.11,а или б. Другое звено, имеющее амплитудно-частотную характеристику как на рис. 4.7,а или б, является звеном верхних частот (a<Y).

Подъем на амплитудно-частотной характеристике на рис. 3.11,а и 4.7,а

(6.17) и при р=К определяется следующим, образом:

1/, K(s + <\)

2р /(a Y)l+ap= р К 4y -Р= -

и расположен на частоте

/2у(а-у)-ар= \т-и\ 2 (а -Y)-bP= •>

На постоянном токе значение амплитудно-частотной характеристики равно IpI«/y. а ее нулевое значение для всех четырех случаев (см. рис. З.П и 4.7) расположено иа частоте fz=feУ

Методики настройки отдельных полосно-заграждающих схем будут приведены далее.

6.7. ОБЩИЕ СВЕДЕНИЯ ПО РАСЧЕТУ И ПОСТРОЕНИЮ ПОЛОСНО-ЗАГРАЖДАЮЩЕГО ФИЛЬТРА

Существует в основном четыре типа пояосно-заграждающих фильтровых звеньев второго порядка, с которыми приходится иметь дело при построении полосно-заграждающего фильтра. Передаточная функция каждого из этих типов подобна функции

Параметры «, Р и y различны догя каждого из этих четырех типов.

Тип I представляет собой полосно-заграждающий фильтр второго порядка, состоящий из единственного звена с я=у=1 и p=l/Q.

Тип II - это звено, соответствующее звену нижних частот первого порядка, для которого 0==1 и P=1/CQ, где С - нормированный коэффициент соответствующей функции нижних частот первого порядка,, приведенный в приложениях А, Б или В. Этот тип представляет собой звено в полосно-заграждающих фильтрах высокого, порядка Баттерворта, Чебышева, инверсных Чебышева и эллиптических.

Тип III получается из звеньев нижних частот второго порядка фильтров Баттерворта и Чебышева. Каждому звену нижних частот второго порядка соответствуют два полосно-заграждающих звена. Первое звено имеет а=1, p=Di/£i и у=1/5ь а второе -а=1, P=l/Di£i и \=l/Di, где El и Dl определяются из (6.11) и (6.12) и зависят от коэффициентов нижних частот В и С, приведенных в приложении А.

Тип IV получается из звеньев нижних частот второго порядка инверсных Чебышева или эллиптических фильтров. Подобно типу III, каждому звену нижних частот соответствуют два полосно-заграждающих звена. Первое звено имеет а=Л2, p=£i/£i и y=Di, а второе -а=1/Л2, P=l/Di£, и y=llDi, где El, Dl и Лг, определяемые уравнениями (6.11), (6.12) и (6.16), зависят от коэффициентов нижних частот Л В и С, приведенных в приложении Б или В.

Как и для полосно-пропускающих фильтров, полосно-заграждающие фильтры создаются на основе каскадного соединения реализованных звеньев второго порядка! Например, полосно-заграждающий эллиптический фильтр шестого порядка соответствует эллиптическому фильтру нижних частот третьего порядка, образованному из одного звена первого и одного звена второго порядка. Следовательно, полосно-заграждающий фильтр будет состоять из-одного звена типа II, соответствующего звену нижних частот первого порядка, соединенного каскадно с двумя звеньями типа IV, полученных из звена нижних частот второго порядка.

Рассмотренные в § 6.4 и 6.5 полосно-заграждающие фильтры второго порядка с мое и на ИНУН можно использовать для реализации только передаточных функций типов I и II, так как эти схемы соответствуют условию a=Y=l. Однако эллиптические функции нижних частот, приведенные в гл. 3, имеют тот же самый вид, что и полосно-заграждающие функции типа.