второе

а=1; p = l/Z)i£,; =1/1)2,;

для фильтров в п. г также соответствуют два звена. Первое звено имеет

а=Л2; fDi/Ei; у=/)2,;

второе

a=l/At; P=1/I»,J?,; Y=l№,

Л=1 +-2(i+Vi + W);

•[1+4CQ= +

+ K(l-f 4CQ=)=-(2SQ)=j;

Если коэффициент усиления К и добротность (Q для пп. а, б и El для пп. в, г) имеют небольшие значения, допустим, не более 10, то приемлемые значения этих произвольных элементов равны

С2=С,; /?4=l/<BoCi.

Если добротность и/или тс имеют, высокие значения, допустим, более 10, то Сг и /?4 должны выбираться таким образом, чтобы сохранился небольшой разброс значений сопротивлений.

3. Выбрать номинальные значения сопротивлений и емкостей как можно ближе к вычисленным значениям и реализовать фильтр или его звенья в соответствии со схемой, показанной на рис. 6.9.

Комментарии

а. Комментарии пп. а, б и д для фильтра с МОС в § 6.8 используются непосредственно, за исключением того, что в п. б сопротивление Req каждого ОУ определяется значением сопротивлений Ri или Rt, соединенных с его инвертирующим входом.

б. Эта схема может использоваться как для низких, так и для высоких значений добротности Q (или El), верхний предел

которых Qsi;100.

в. Настройка осуществляется как описано в § 6.6, а именно: сначала, изменяя сопротивление Ri, добиваются максимального подавления на частоте fz, а затем, изменяя сопротивление Rz, размещают подъем амплитудно-частотной характеристики на частоте fm и, наконец, с помощью сопротивления /?з выставляют необходимое значение Km- Для низкодобротных звеньев последние два этапа можно при необходимости повторить.

г. Эта схема обладает инвертирующим коэффициентом усиления -К {К>0).

Схема на трех конденсаторах была рассмотрена в § 3.4.

6.12. РАСЧЕТ БИКВАДРАТНОГО

ЭЛЛИПТИЧЕСКОГО ПОЛОСНО-ЗАГРАЖДАЮЩЕГО ФИЛЬТРА

Схему биквадратного эллиптического полосно-заграждающего фильтра (рис. 6.10) можно использовать для реализации а) полосно-заграждающего фильтра второго порядка и звеньев фильтра высокого порядка, а именно б) полосно-заграждающего звена второго порядка, соответствующего звену нижних частот первого порядка фильтра Баттерворта, Чебышева, инверсного Чебышева и эллиптического, в) двух полосно-заграждающих звеньев второго порядка, соответствующих звену нижних частот второго порядка фильтра Баттерворта или Чебышева или г) двух полосно-заграждающих звеньев второго порядка, соответствующих звену нижних частот второго порядка инверсного Чебышева или эллиптического фильтра. Для расчета этого фильтра или его звеньев, обладающих заданной центральной частотой fo (Гц), или coo=2nfo (рад/с), коэффициентом усиления К, добротностью Q, а для инверсных Чебышева и эллиптических фильтров и минимальным затуханием в полосе задерживания (MSL), для эллиптических фильтров еще и неравномерностью передачи в полосе пропускания (PRW), необходимо выполнить следующие шаги.

1. Для расчета п. б найти значение-нормированного коэффициента С звена нижних частот первого порядка из соответствующей таблицы в приложении А, Б или В; для п. в найти значения нормированных коэффициентов нижних частот В и С из-соответствующей таблицы в приложении А; для п. г найти значения нормированных коэффициентов нижних частот А, В и С из соответствующей таблицы в приложении Б или В.

2. Выбрать номинальное значение емкости Cl (предпочтительно близкое к значению 10/fo мкФ) и вычислить сопротивления

i?i = l/KPcooCi; R2=KRi:

R,= 1/Ксо„С.; R = R,jK;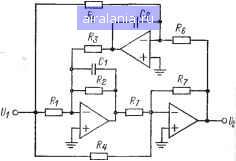

Рис. 6.10. Схема биквадратного эллиптического полосно-заграждающего фильтра.

где Сг и Rt имеют произвольные значения. Для п. а

a=Y=l; P=l/Q;

для п. б

a=Y=l; P=1/CQ;

для фильтров в п. в соответствуют два звена. Первое звено имеет

а=1; p=D,/£,; ==2,; второе

а=1; р=1/ад; =1/5=1;

для фильтров в п. г также соответствуют два звена. Первое звено имеет

второе

0=1/2; §=l/DtEu \=\ID\,

1 / С-*

+ l/(l + 4CQ=)2 (2BQ)2];

qc {qC )

Если коэффициент усиления К и добротность (Q для пп. а, б и £i для пп. в,

г) имеют небольшие значения, например

не более 10, то

С2=С,; /?7=1/«оС,.

Если добротность Q(Ei) и/или коэффициент усиления К имеют высокие значения, например более 10, то С2 и Rr должны выбираться таким образом, чтобы сохранился небольшой разброс значений сопротивлений.

3. Выбрать номинальные значения сопротивлений и емкостей как можно ближе-к вычисленным значениям и реализовать, фильтр или его звенья в соответствии со. схемой, показанной на рис. 6.10.

Комментарии

а. Комментарии пп. а, б и д для фильтра с МОС в § 6.8 используются непосредственно, за исключением того, что в. п. б сопротивление Reg каждого ОУ определяется значением сопротивления iRi, Re. или Ri, соединенного с его входным контактом.

б. Эта схема может использоваться; как для высоких, так и для низких значений добротности Q (или £1) с помощью, выбора произвольных параметров на шаге 2 таким образом, чтобы сохранить относительно небольшой разброс значений сопротивлений. Для небольших коэффициентов усиления значения Q (или £1) могут достигать 100.

в. Настройка осуществляется путем-изменения сопротивлений Ri, - добиваются максимального подавления на частоте-fz; Rs - устанавливают центральную частоту; Ri - добротность Q и /?1 или /?5 -коэффициент усиления (см. § 6.6).

г. Эта схема обладает инвертирующи!* коэффициентом усиления K=iR2/Ri-

Биквадратный эллиптический фильтр> был рассмотрен в § 3.5.

ГЛАВА СЕДЬМАЯ ВСЕПРОПУСКАЮЩИЕ ФИЛЬТРЫ И ФИЛЬТРЫ С ПОСТОЯННЫМ ВРЕМЕНЕМ ЗАМЕДЛЕНИЯ

7.1. ВСЕПРОПУСКАЮЩИЕ ФИЛЬТРЫ

Ранее в основном рассматривались частотно-избирательиые фильтры, для которых наиболее важным параметром является амплитудно-частотная характеристика. В этой главе будут даиы другие типы фильтров, для которых основной интерес представляет фазо-частотиая характеристика и/или соответствующее ей время замедления.

Первым рассматривается всепропу-скающий или фазосдвигающий фильтр, который обладает постоянной амплитудно-частотной характеристикой \И{])\=:К и фазо-частотиой характеристикой Ч)(ш), являющейся функцией частоты. На рис. 7.1 изображена типовая фазо-частотная харак-

теристика, из которой можно показать, чтс если фо--фаза или фазовый сдвиг на частоте т (рад/с) или fo=(uo/2n (Гц), то

<р(сао)=<Ро.

Поскольку рассматриваемая передаточная функция определяется соотношением H=V2lVu то фазовый сдвиг фо на частоте О)=сао представляет собой разность, между фазами напряжений и Vi. Таким образом, фаза выходного напряжения-Vj. больше фазы входного напряжения Fi на чРв градусов. Если оба напряжения имеют синусоидальную форму, то выходной, сигнал достигает своих максимальных ила минимальных значений на фо градусов или„ если фо выражено в радианах, на фв/юр. секунд раньше входного сигнала. Следова-

I, рад/с

Рис. 7.1. Типовая фазо-частотная характеристика.

тельно, выходной сигнал опережает входной (или входной сигнал отстает от выходного) на фо. (Однако в большинстве случаев фо имеет отрицательное значение, так что в действительности выходной сиг-нал отстает от входного на положительный угол.)

Разница в секундах фо/«о между дву-мя соседними максимальными значениями входного и выходного, сигналов тождественна времени замедления, которое было определено в § 1.2. Эта характеристика .важна для времязамедляющих фильтров, таких, как фильтр Бесселя, где основной акцент делается на получение времен за-шедления, оче.Ь близких к постоянному -.значению. Этот тип фильтров будет описан в последней части данной главы.

Рассматриваются исключительно всепропускающие фильтры второго порядка, для которых передаточная функция имеет ивид:

„ V. /С(=-йш,5-ЬЬО

К, s2,-{ аю„8 + 6ь>=о

>тде К, а и b представляют собой выбранные определенным образом постоянные числа, а <Оо - интересующая нас частота. Для фильтров, описываемых уравнением (7.1), получаем, как и требовалось, Я(/(в)=7С, а фазо-частотная характери-•стика определяется следующим образом:

у (со) = - 2 arctg

flco„to

(7.2)

Постоянное число К, задающее коэф-.фициент усиления фильтра, и определяю-.:щие фазовый сдвиг коэффициенты а и b выбираются исходя из предъявленных к фильтру требований. Подобно другим типам фильтров добротность С также определяется соотношением Q=16/o.

Очевидно, что если ф((йо)=фо является точно установленным фазовым сдвигом на частоте мо. то из (7.2) получаем

фо=-2arctg f а/ (6-1) ]

(7.3)

V, следовательно, имеются два параметра а и 6, которые используются для формирования заданного условия фо. Таким образом, получен добавочный параметр, который можно использовать для определения дополнительного условия, например для за-

дания коэффициента усиления фильтра или для минимизации смещения ОУ по постоянному току.

7.2. ВСЕПРОПУСКАЮЩИЕ ФИЛЬТРЫ С МНОГОПЕТЛЕВОИ ОБРАТНОЙ СВЯЗЬЮ

Схема, реализующая всепропускающую функцию второго порядка, (7.1) изображена на рис. 7.2 и представляет собой схему с многопетлевой обратной связью (МОС). Всепропускагощая функция типа (7.1) достигается при

ясо„ = 2/;?2С,; 1

b(o\=\/RiR2C\; \ (7.4)

KRJ(R, + Ri) )

и условии, что

4RiRi=R2Rs. (7.5)

Очевидно, что значение коэффициента усиления К ограничено, т. е.

0<К<1. (7.6)

Кроме того, если желательно минимизировать смещение ОУ по постоянному току, то

«3/?4/(i?3-H?4)=?2. (7.7)

Из (7.4) и (7.5) получаем

K=b/(b+a). (7.8)

Таким образом, для заданных фо= =ф(«о) и К из (7.3) и (7.8) следует, что

для 0<фо<180°

+ Vl-f- [4Д/(1-К)1 tg= (у,/2)} °= 2Ktg(y„/2)

(T8J

для -180° <¥с<0

(1-К) {-1-

-Vi + i4K/{i-K)tg (ъ/т

2Ktg (у„/2)

(7.10) (7. II)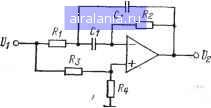

Рис. 7.2. Схема всепропускающего фильтра с многопетлевой обратной связью.