ГЛАВА ВТОРАЯ ФИЛЬТРЫ нижних ЧАСТОТ БАТТЕРВОРТА И ЧЕБЫШЕВАс

2.1. ФИЛЬТРЫ НИЖНИХ ЧАСТОТ

Фильтр нижних частот представляет собой устройство, которое пропускает сигналы, низких частот и задерживает сигналы высоких частот. В общем "случае определим полосу пропускания как интервал частот 0<со<и)с, полосу задерживания как частоты co>coi, переходную область как диапазон частот cOc<co<coi (сОс - частота среза). Эти частоты обозначены на рис. 2.1, на котором приведена реальная амплитудно-частотная характеристика фильтра нижних частот, где в данном случае заштрихованные области представляют собой допустимые отклонения характеристики в полосах пропускания и задерживания.

Если минимальное затухание выбрать за нормированный уровень О (А = \ на рис. 2.1), то логарифмическая характеристика фильтра нижних частот имеет вид, изображенный на рис. 2.2. Максимальное затухание в децибелах в полосе пропускания составляет аь а минимальное затухание в полосе задерживания ог (А я А2 - соответственно значения амплитудно-частотной характеристики). Затухание ai ие может превышать 3 дБ, в то время как типовое значение Ог значительно больше и может находиться в пределах 20:0? 100 дБ (в этом случае имеем 0,1Л2> ,00001).

Коэффициент усиления фильтра нижних частот представляет собой значение его

WJuj)\

щ,рад/с

Рис. 2.1. Реальная амплитудно-частотная характеристика фильтра нижних частот.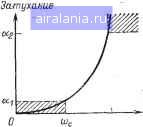

Рис. 2.2. Логарифмическая характеристика фильтра нижних частот.

передаточной функции при s=0 или, что эквивалентно, значение его амплитудно-частотной характеристики на частоте сй=0. Следовательно, коэффициент усиления- реального фильтра с амплитудно-частотной характеристикой, показанной на рис.: 2.1, равен А.

Существует много типов фильтров йиж-них частот, удовлетворяющих данному .;на-бору технических требований, таких, как А, Al, Л2, СОс и С0[, обозначенных на рис. 2.1, или Oi, «2, ©с и 6)1-на рис. 2.2: Фильтры. Баттерворта, Чебышева, тверсные Чебы-шева и эллиптические -.образуют четыре наиболее известных класса. Фильтр Баттерворта обладает монотрнной характеристикой, подобной характеристике на рис. 2.1 и 2.2. (Характеристика являете? монотонно спадающей, если она никогда не возрастает с увеличением частоты.) Характеристика фильтра Чебышева. содержит пульсации (колебания передачи) в полосе пропускания и MOHOixDHHa в полосе задерживания. На рис. 2.3 изображен вид характеристики фильтра Чебышева шестого порядка. Инверсная характеристика фильтра Чебышева монотонна в полосе, пропускания и обладает пульсациями в полосе задержи-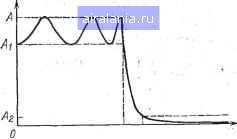

Рис. 2.3. Амплитудно-частотная характеристика фильтра Чебышева шестого порядка.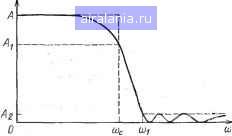

Рис, 2.4. .Амплитудно-частотная характеристика инверсного фильтра Чебышева шестого порядка.

A A,

Рис. 2.5. Амплитудно-частотная характеристика эллиптического фильтра шестого порядка.

вания. Пример характеристики фильтра шестого порядка приведен на рис. 2.4. Наконец, характеристика эллиптического фильтра обладает пульсациями как в полосе пропускания, так и в полосе задерживания, а ее вид для фильтра шестого порядка изображен на рис. 2.5.

Амплитудно-частотная характеристика оптимального фильтра нижних частот удовлетворяет обозначенным на рис. 2.1 (или на рис. 2.2) условиям для данного порядка п и допустимого отклонения в полосах пропускания и задерживания при минимальной ширине переходной области. Таким образом, если заданы значения Л, Л,, Лг, п и сос, то значение чаихэты coj минимально. Для полиномиальной характеристики оптимальной является характеристика фильтра Чебышева [25]. Однако в общем случае оптимальным является эллиптический фильтр J24], характеристики которого значительно лучше характеристик фильтра Чебышева.

В последующих параграфах кратко рассматриваются фильтры Баттерворта и Чебышева, представляющие собой наиболее хорошо изученные типы полиномиальных фильтров. Фильтры инверсные Чебышева и эллиптические, обладающие более общими передаточными функциями, рассмотрены в гл. 3. Книги по схемотехнике и фильтрам Г32, 33, 5, 16, 29, 4, 6] рекомендуются читателям для дальнейшего изучения материала.

2.2. ФИЛЬТРЫ БАТТЕРВОРТА

Вероятно, наиболее простая амплитудно-частотная характеристика фильтра нижних частот у фильтра Баттерворта [33], которая в случае л-го порядка определяется следующим образом:

\Н (iv>) I = (п = 1, 2, 3...).

(2.1)

Эта характеристика фильтра Баттерворта монотонно спадает (никогда не возрастает) при увеличении частоты. Увеличе-

ние порядка также приводит к улучшению характеристики, что можно видеть из рис. 2.6, где для Л = 1 изображены некоторые характеристики фильтра Баттерворта.

Фильтр Баетерворта представляет собой полиномиальный филыр и в общем случае обладает передаточной функцией вида

(2.2)

где /(-постоянное число. Для нормированного фильтра,.т. е. при сйс=1 рад/с, передаточную функцию можно записать в виде произведения сомножителей для №=2, 4, 6 ... как

или для п=3, 5, 7 ... как

j=!o ТТ пл.

I/. s-ffc„ 11 s + a-bk - k=i

В обоих случаях коэффициенты задаются при fco=l и для k=\, 2 ... следующим образом:

„ (2fe- l)7t

= 2sin--; bfe = 1.

(2.5)

Очевидно, что коэффициент усиления фильтра Баттерворта, описываемого уравнением (2.2), равен К (значению передаточной функции при s=0). Если фильтр построен на основе каскадного соединения звеньев, соответствующих сомножителям в (2.3) или (2.4), то Л ft и/или Ло будут представлять собой коэффициент усиления звена. Таким образом, коэффициент усиления фильтра равен произведению коэффициентов усиления отдельных звеньев.

Амплитудно-час1хэтная характеристика фильтра Баттерворта наиболее плоская около частоты сй=0 по сравнению с характеристикой любого полиномиального фильтра п-го порядка и вследствие этого назы-

\H(jw)\

Рис. 2.6. Амплитудно-частотные характеристики фильтра Баттерворта нижних частот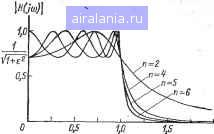

2fiw

Рис. 2.8. Амплитудно-частотные характеристики фильтра Чебышева нижних частот.

Рис. 2.7. Амплитудно-частотная характеристика реального фильтра Баттерворта шестого порядка.

вается максимально плоской. Следовательно, для диапазона низких частот характеристика фильтра Баттерворта наилучшим образом аппроксимирует идеальную характеристику. Однако для частот, расположенных около точки среза и в полосе задерживания, характеристика фильтра Баттерворта заметно уступает характеристике фильтра Чебышева, который рассматривается в следующем параграфе.

Однако фазо-частотная характеристика фильтра Баттерворта лучше (более близка к линейной), чем соответствующие фазо-частотные характеристики фильтров Чебышева, инверсных Чебышева и эллиптических сравнимого порядка [32, 33]. Это согласуется с общим правилом для фильтров данного типа - чем лучше амплитудно-частотная характеристика, тем хуже фазо-частотная, и наоборот.

Передаточная функция нормированного фильтра Баттерворта (2.2) для п=2, 3, ... ..., 10 приведена в приложении А в виде произведения сомножителей (2.3) и (2.4).

Амплитудно-частотная характеристика лабораторного образца фильтра Баттерворта нижних частот шестого порядка показана на рис. 2.7.

2.3. ФИЛЬТРЫ ЧЕБЫШЕВА

Как было отмечено ранее, фильтр Че-бышева нижних частот представляет собой оптимальный полиномиальный фильтр. Он обладает амплитудно-частотной характеристикой [32], которая определяется следующим образом:

Vl-(-e=C=„ (со/со,) = 1, 2, 3...).

(2.6)

Параметры е и К - постоянные числа, а Сп является полиномом Чебышева первого рода степени п и имеет вид:

Сп (л:)=со8 (п arccos х). (2.7)

Амплитудно-частотная характеристика достигает своего наибольшего значения К в тех точках, где С„ равно нулю. Поскольку эти точки распределены по полосе пропускания, то характеристика фильтра Чебышева содержит пульсации в полосе пропускания и монотонна в других областях. Размах этих пульсаций определяет параметр е, а их число степень п. Коэффициент усиления фильтра определяется значением К. На рис. 2.8 изображены некоторые характеристики фильтра Чебышева для К=1 и сйс=1 рад/с.

Фильтр Чебышева иногда называют равноволновым фильтром, поскольку все пульсации равны по значению. Для K-l (рис. 2.8), размах пульсаций

RW=l-,-7=4=-. (2.8)

1 +

Таким образом, как угодно можно уменьшить RW, выбрав значение параметра 8 достаточно малым.

Минимально допустимое затухание в полосе пропускания - постоянный размах пульсаций, часто выражается в децибелах как

-201og,„ (1/ГГТ1Щ= = 10 log,o(l-f е»). • (2.9)

и может использоваться как характеристика фильтра Чебышева. Например, фильтр с неравномерностью передачи 1/2 дБ обладает таким значением е, что а=1 /2 (это дает 8= 0,3493). В общем случае, решая уравнение (2.9) относительно 8, можно получить

e = "l/lO«/JO-1. (2.10)

Наибольшим допустимым размахом пульсаций обладает фильтр Чебышева с неравномерностью передачи 3 дБ, для которого в (2.9) 8=1 (если говорить более точно, то необходимо иметь значение е= =0,99763, поскольку log 2 не равен точно 0,3).

По амплитудно-частотным характеристикам на рис. 2.1 и 2.8 определяем Л=1, а Ai=:i/Vl-\-e. Для данного случая также можно точно определить А, которое установило бы значение частоты coi. Частота Шс=1 рад/с представляет собой точку